Matières
Niveaux
La formule quadratique permet de résoudre une équation polynomiale de degré 2 de la forme |ax^2+bx+c=0| où |a \not= 0.|
||x_{1,2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}||
Ramener l’équation de degré 2 sous la forme |ax^2+bx+c=0| afin de déterminer |a,| |b| et |c.|
Remplacer |a,| |b| et |c| dans la formule quadratique et effectuer le calcul.
Donner les solutions.
Lors de la résolution, le symbole |\pm| indique qu’on doit séparer cette formule en 2 : une avec le |+| et l’autre avec le |-.|
||\begin{align}x_1&=\dfrac{-b\color{#ec0000}+\sqrt{b^2-4ac}}{2a}\\\\x_2&=\dfrac{-b\color{#ec0000}-\sqrt{b^2-4ac}}{2a}\end{align}||
Résous l’équation |-5x^2+3{,}5x-1=-4.|
Ramener l’équation sous la forme |ax^2+bx+c=0| afin de déterminer |a,| |b| et |c|
||\begin{aligned}-5x^2+3{,}5x-1&=-4\\\color{#ec0000}{-5}x^2+\color{#3b87cd}{3{,}5}x+\color{#3a9a38}3&=0\end{aligned}\\\\
\begin{aligned}\\\color{#ec0000}a=\color{#ec0000}{-5}, \ \color{#3b87cd}b=\color{#3b87cd}{3{,}5},\ \color{#3a9a38}c=\color{#3a9a38}3\end{aligned}||
Remplacer |a,| |b| et |c| dans la formule quadratique et effectuer le calcul
||\begin{align}x_{1,2}&=\dfrac{-\color{#3b87cd}b\pm\sqrt{\color{#3b87cd}b^2-4\color{#ec0000}a\color{#3a9a38}c}}{2\color{#ec0000}a}\\&=\dfrac{-\color{#3b87cd}{3{,}5}\pm\sqrt{\color{#3b87cd}{3{,}5}^2-4(\color{#ec0000}{-5})(\color{#3a9a38}3)}}{2(\color{#ec0000}{-5})}\\&=\dfrac{-3{,}5\pm\sqrt{12{,}25+60}}{-10}\\&=\dfrac{-3{,}5\pm\sqrt{72{,}25}}{-10}\\&=\dfrac{-3{,}5\pm8{,}5}{-10}\end{align}|| ||\begin{aligned}x_1&=\dfrac{-3{,}5+8{,}5}{-10} \\&=\dfrac{5}{-10}\\&=-0{,}5\end{aligned}\qquad\begin{aligned}x_2&=\dfrac{-3{,}5-8{,}5}{-10}\\&=\dfrac{-12}{-10}\\&=1{,}2\end{aligned}||
Donner les solutions
Les solutions de l’équation |-4=-5x^2+3{,}5x-1| sont |-0{,}5| et |1{,}2.|
Le graphique ci-contre montre que la parabole d’équation |f(x)=-5x^2+3{,}5x-1| croise la droite d’équation |\color{#ff55c3}{y=-4}| à 2 endroits : à |x=-0{,}5| et à |x=1{,}2.|
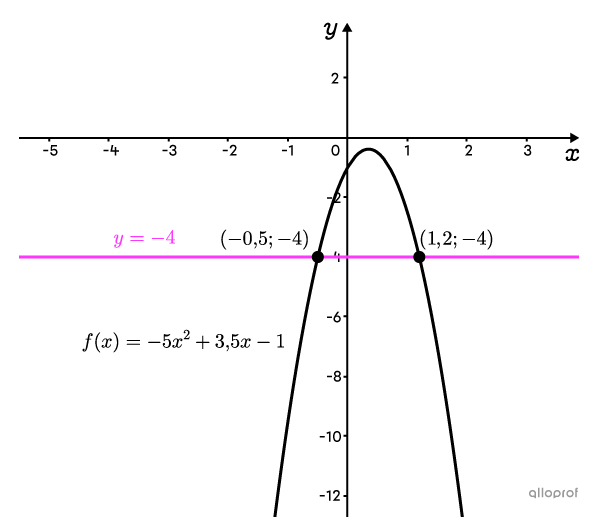
Voici un exemple où on utilise la formule quadratique pour trouver les zéros d’une fonction polynomiale de degré 2.
Trouve les zéros de la fonction polynomiale de degré 2 dont l’équation est |f(x)=-3x^2+8x-10.|
Quand on cherche les zéros d’une fonction, on remplace |f(x)| par |0| et on isole |x.|||\begin{align} f(x)&=-3x^2+8x-10\\0&=-3x^2+8x-10\end{align}||
Ramener l’équation sous la forme |ax^2+bx+c=0| afin de déterminer |a,| |b| et |c|
L’équation est déjà sous la bonne forme.||\begin{align}0&=\color{#ec0000}{-3}x^2+\color{#3b87cd}8x\color{#3a9a38}{-10}\\\\ \color{#ec0000}a&=\color{#ec0000}{-3}, \ \color{#3b87cd}b=\color{#3b87cd}{8},\ \color{#3a9a38}c=\color{#3a9a38}{-10}\end{align}||
Remplacer |a,| |b| et |c| dans la formule quadratique et effectuer le calcul
||\begin{align}x_{1,2}&=\dfrac{-\color{#3b87cd}b\pm\sqrt{\color{#3b87cd}b^2-4\color{#ec0000}a\color{#3a9a38}c}}{2\color{#ec0000}a}\\
&=\dfrac{-\color{#3b87cd}8\pm\sqrt{\color{#3b87cd}8^2-4(\color{#ec0000}{-3})(\color{#3a9a38}{-10})}}{2(\color{#ec0000}{-3})}\\&=\dfrac{-8\pm\sqrt{64-120}}{-6}\\&=\dfrac{-8\pm\sqrt{-56}}{-6}\end{align}||Comme il est impossible d’extraire la racine carrée d’un nombre négatif, on arrête le calcul ici et on en déduit que la fonction n’a pas de zéro.
Donner la solution
La fonction |f(x)=-3x^2+8x-10| n’a pas de zéro.
Le graphique ci-contre montre que la parabole d’équation |f(x)=-3x^2+8x-10| ne croise pas l’axe des |\color{#ff55c3}{x}| puisqu’elle passe complètement en dessous de celui-ci.
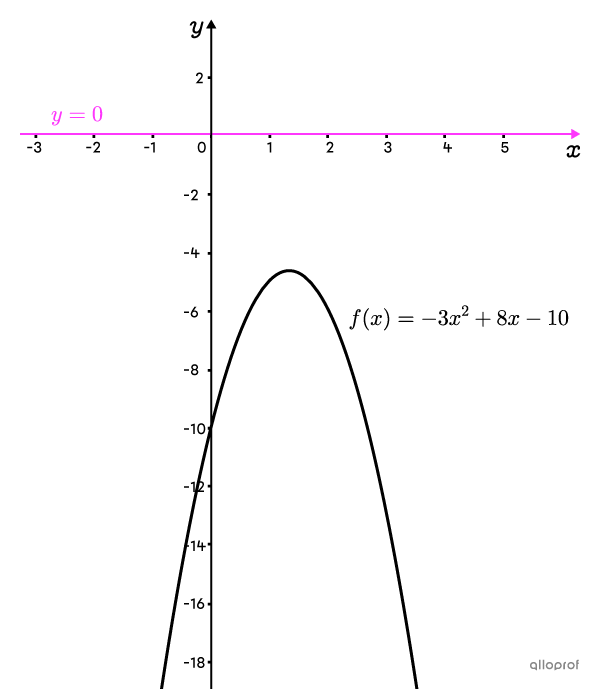
Le discriminant |(\Delta)| est l’expression qui se trouve sous la racine (le radicande) dans la formule quadratique.||\begin{align}x_{1,2}&=\dfrac{-b\pm\sqrt{\color{#333fb1}{\Delta}}}{2a}\\x_{1,2}&=\dfrac{-b\pm\sqrt{\color{#333fb1}{b^2-4ac}}}{2a}\end{align}||Il est important de bien comprendre le lien entre le discriminant du trinôme |ax^2+bx+c| et le nombre de solutions à l’équation |ax^2+bx+c=0.|
|
|b^2-4ac>0| |
L’équation possède 2 solutions distinctes. |
|
|b^2-4ac=0| |
L’équation possède une seule solution. |
|
|b^2-4ac<0| |
L’équation ne possède pas de solution. |
Voici un exemple où l’équation a une solution.
Résous l’équation |2x^2-4x+1=-1.|
Ramener l’équation sous la forme |ax^2+bx+c=0| afin de déterminer |a,| |b| et |c|
||\begin{aligned}2x^2-4x+1&=-1\\\color{#ec0000}2x^2\color{#3b87cd}{-4}x+\color{#3a9a38}2&=0\end{aligned}\\\\
\begin{aligned}\\\color{#ec0000}a=\color{#ec0000}{2}, \ \color{#3b87cd}b=\color{#3b87cd}{-4},\ \color{#3a9a38}c=\color{#3a9a38}2\end{aligned}||
Remplacer |a,| |b| et |c| dans la formule quadratique et effectuer le calcul
||\begin{align}x_{1,2}&=\dfrac{-\color{#3b87cd}b\pm\sqrt{\color{#3b87cd}b^2-4\color{#ec0000}a\color{#3a9a38}c}}{2\color{#ec0000}a}\\
&=\dfrac{-(\color{#3b87cd}{-4})\pm\sqrt{(\color{#3b87cd}{-4})^2-4(\color{#ec0000}{2})(\color{#3a9a38}{2})}}{2(\color{#ec0000}{2})}\\&=\dfrac{4\pm\sqrt{16-16}}{4}\\&=\dfrac{4\pm\sqrt{0}}{4}\\&=\dfrac{4\pm 0}{4}\\&=\dfrac{4}{4}\\&=1\end{align}||Comme le calcul sous la racine carrée donne |0,| on obtient |\pm 0.| Il n’est donc plus nécessaire de séparer l’équation en 2, car elle n’a qu’une seule solution.
Donner la solution
La solution de l’équation |2x^2-4x+1=-1| est |x=1.|
Le graphique ci-contre montre que la droite d’équation |\color{#ff55c3}{y=-1}| passe par le sommet de la parabole |f(x)=2x^2-4x+1.| C’est pourquoi il n’y a qu’une seule solution.

Voici la démonstration de la formule quadratique.
Soit l’équation |ax^2+bx+c=0.| Pour en faire la démonstration, il faut isoler |x.| Pour y arriver, on utilise la complétion du carré. On débute en mettant |a| en évidence.||a\left(x^2+\dfrac{b}{a}x+\dfrac{c}{a}\right)=0||On peut diviser les 2 membres de l'égalité par |a,| car ce dernier est différent de |0.|||x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0||On poursuit en ajoutant et en soustrayant le terme |\left(\dfrac{\frac{b}{a}}{2}\right)^2| à gauche de l’équation. On obtient :||\begin{align}x^2+\dfrac{b}{a}x\color{#3a9a38}{+\left( \dfrac{\frac{b}{a}}{2} \right)^2}+\dfrac{c}{a}\color{#3a9a38}{- \left( \dfrac{\frac{b}{a}}{2} \right)^2}=0\\x^2+\dfrac{b}{a}x\color{#3a9a38}{+\dfrac{b^2}{4a^2}}+\dfrac{c}{a}\color{#3a9a38}{- \dfrac{b^2}{4a^2}}=0\end{align}||Les 3 premiers termes du membre de gauche peuvent être factorisés puisqu'ils forment un trinôme carré parfait.||\left(x+\dfrac{b}{2a}\right)^2+\dfrac{c}{a}-\dfrac{b^2}{4a^2}=0||On met les 2 derniers termes sur un dénominateur commun.||\left(x+\dfrac{b}{2a}\right)^2+\dfrac{4ac-b^2}{4a^2}=0||On soustrait la fraction de chaque côté de l'égalité.
||\left(x+\dfrac{b}{2a}\right)^2=-\left(\dfrac{4ac-b^2}{4a^2}\right)||On distribue le |-| devant la fraction aux 2 termes du numérateur.||\left(x+\dfrac{b}{2a}\right)^2=\dfrac{b^2-4ac}{4a^2}||On extrait la racine carrée des 2 côtés de l'égalité. Il ne faut pas oublier le symbole |\pm| du côté droit.||\begin{align}\color{#ec0000}{\sqrt{\color{black}{\left(x+\dfrac{b}{2a}\right)^2}}} &=\color{#ec0000}{\sqrt{\color{black}{\dfrac{b^2-4ac}{4a^2}}}}\\x+\dfrac{b}{2a}&=\pm \dfrac{\sqrt{b^2-4ac}}{2a}\end{align}||Il ne reste qu’à isoler |x.|||x=-\dfrac{b}{2a}\pm\dfrac{\sqrt{b^2-4ac}}{2a}||On regroupe les 2 fractions.||x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}||On obtient bel et bien la formule quadratique.