Secondaire 5 • 1a
Bonjour, je suis bloqué à ce numéro-ci…
Je ne sais pas comment poursuivre la simplification
Numéro k). Aussi, j’avais une autre question, est ce que c’est permis d’avoir une racine carrée au dénominateur? Quand il y en a une, est ce que on doit automatiquement s’en débarrasser en multipliant la fraction par la racine carré présente au dénominateur? Merci!!!
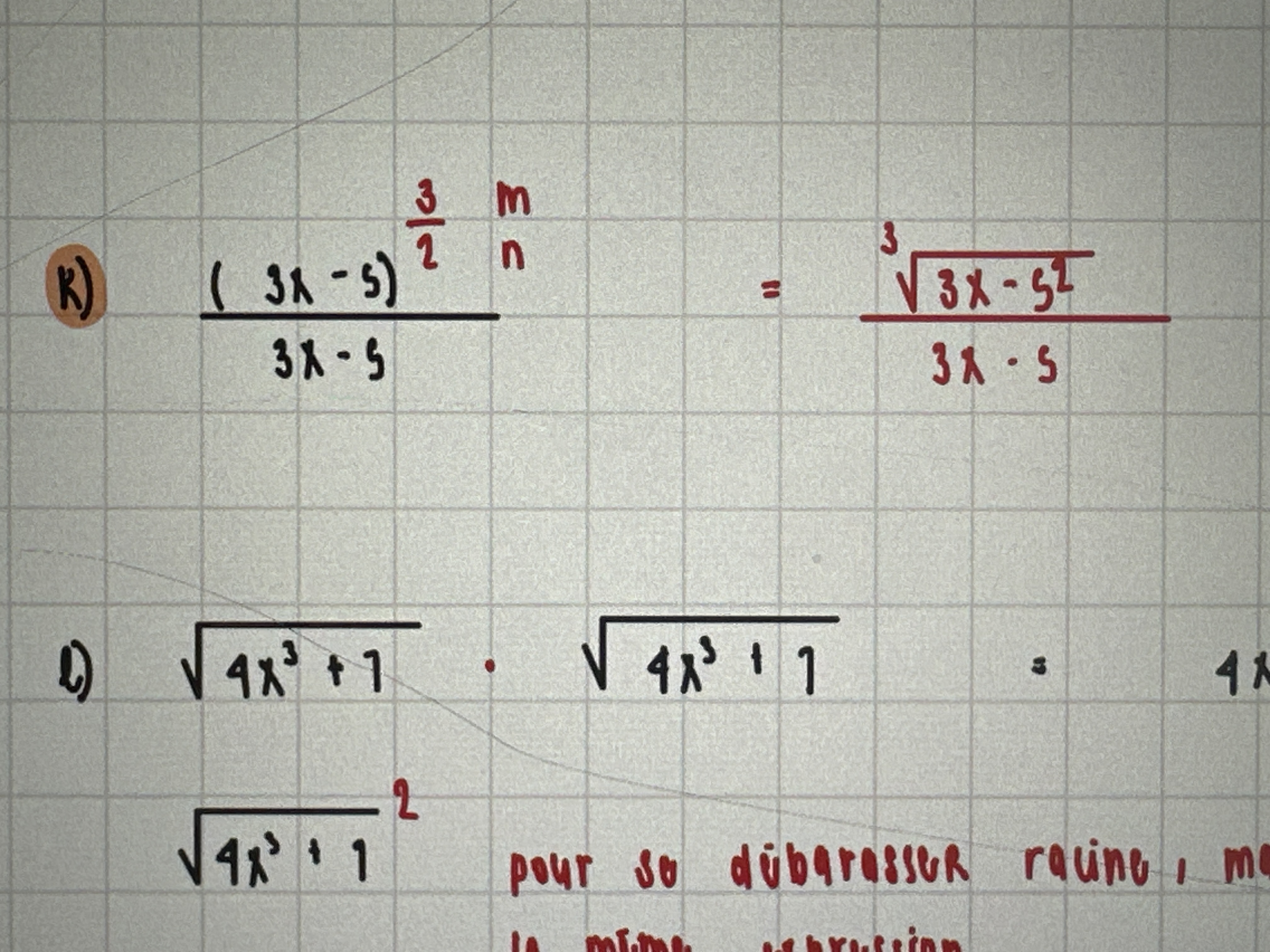






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
Tu dois utiliser les lois des exposants, en particulier celles-ci :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Tu auras donc ceci :
$$ \frac{(3x-5)^{\frac{3}{2}}}{3x-5}$$
$$ \frac{(3x-5)^{\frac{3}{2}}}{(3x-5)^1}$$
$$ (3x-5)^{\frac{3}{2}-1}$$
$$ (3x-5)^{\frac{1}{2}}$$
$$ \sqrt{3x-5}$$
Voilà!
En ce qui concerne ta seconde question, oui, tu dois éliminer la racine carrée au dénominateur. C'est ce qu'on appelle la rationalisation de fraction. Pour cela, tu dois multiplier la fraction par une autre fraction où le numérateur et le dénominateur sont cette racine carrée. Par exemple, si le dénominateur d'une fraction est √3, alors il faut multiplier cette fraction par √3/√3. Attention, tu ne peux pas simplement multiplier par √3, puisque cela change le nombre initial! En multipliant par √3/√3, on ne change pas le résultat, puisqu'on le multiplie simplement par 1 (√3/√3 = 1).
Voici un exemple :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!