Matières
Niveaux
Les vecteurs
Fiche | Mathématiques
Secondaire
5
Pour aborder la notion de vecteur en mathématique, il y a beaucoup de nouveaux termes qui sont importants à maitriser. Par ailleurs, chacun de ces termes ont une définition précise qui peuvent porter à confusion.
Le vecteur
Un vecteur, généralement noté |\overrightarrow u|, est un objet mathématique qui possède à la fois une grandeur, une direction et un sens.
La direction et le sens constituent l'orientation du vecteur.
Par contre, ce n'est pas la seule façon d'identifier un vecteur.
Si |A| représente le point de départ d'un vecteur et |B| son point d'arrivée, on peut utiliser la notation |\overrightarrow {AB}| pour y faire référence.
Tout comme son écriture l'indique, le vecteur est en fait un segment de droite qui possède un point de départ et une flèche pour indiquer son point d'arrivée et son orientation.
Grandeur scalaire
La grandeur scalaire, généralement appelée scalaire, est une grandeur définie par un nombre réel.
En d'autres mots, il s'agit d'un coefficient qu'on applique à un vecteur et à ses composantes.
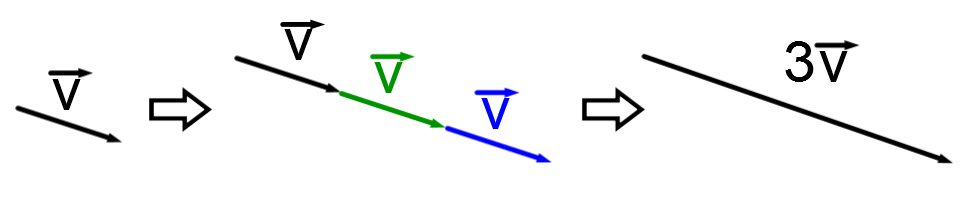
Dans ce cas, la valeur du scalaire est |3|.
Grandeur vectorielle
La grandeur vectorielle est définie par un nombre, un sens et une direction.
Bref, on peut résumer la grandeur vectorielle par une utilisation concrète des vecteurs dans la vie de tous les jours.
Lors d'une croisière, un bateau s'arrête sur plusieurs petites iles afin que les touristes les visitent. Pour se rendre à la deuxième ile, le capitaine doit maintenir le cap en direction nord-ouest à une vitesse de 25 nœuds afin de respecter leur horaire.
Direction, sens et orientation d'un vecteur
L'orientation d'un vecteur fait référence à la direction (droite qui supporte le vecteur) et au sens (flèche) de celui-ci.
Afin de bien distinguer ces trois notions, il est préférable de comparer plusieurs vecteurs ensemble.
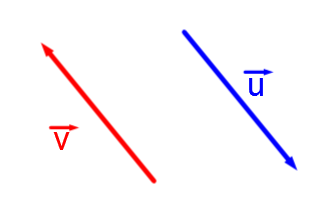
Selon l'inclinaison de la droite qui supporte chacun des vecteurs, on voit que la direction |\color{red}{\overrightarrow v}| est la même que |\color{blue}{\overrightarrow u}|.
Par contre, leur sens est différent puisque les flèches ne pointent pas vers le même endroit.
En identifiant le vecteur par son point de départ et son point d'arrivée, il est plus facile de reconnaitre des vecteurs qui ont la même direction, mais qui sont de sens contraire.
|\overrightarrow {AB}| commence au point |A| et finit au point |B| alors que |\overrightarrow {BA}| commence au point |B| et finit au point |A|.
Norme d'un vecteur
La norme d'un vecteur, aussi appelée le module, notée | \mid \mid \overrightarrow v \mid \mid |, est un nombre réel qui définit la grandeur d'un vecteur.
Un vecteur dont la norme est |1| est appelé un vecteur unitaire.
Un vecteur dont la norme est |0| est appelé un vecteur nul et on le note |\overrightarrow{0}.|
En se référant à la géométrie analytique, il s'agit de la distance entre le point de départ du vecteur et son arrivée.
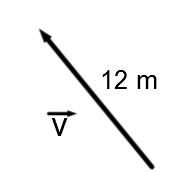
Ainsi, |\mid \mid \overrightarrow v \mid \mid = 12 \text{m}|.
De plus, les vecteurs ne font pas seulement partie du domaine de la mathématique.
Les vecteurs sont également utilisés en Physique. Par contre, l'approche et les notions qui y sont traitées sont légèrement différentes.
Pour valider ta compréhension à propos des vecteurs de façon interactive, consulte la MiniRécup suivante :
