Subjects
Grades
The Relationship Between Volume and Temperature (Charles’s Law)
Concept sheet | Chemistry
Secondary
5
Table of contents
Charles’s Law is a simple gas law.
Charles’s Law
Charles’s law describes the mathematical relationship between the volume |(V)| and the absolute temperature |(T)| of a gas.
To understand the relationship between the volume and the temperature of a gas, we can do the following experiment where the pressure and the quantity of gas are constant.
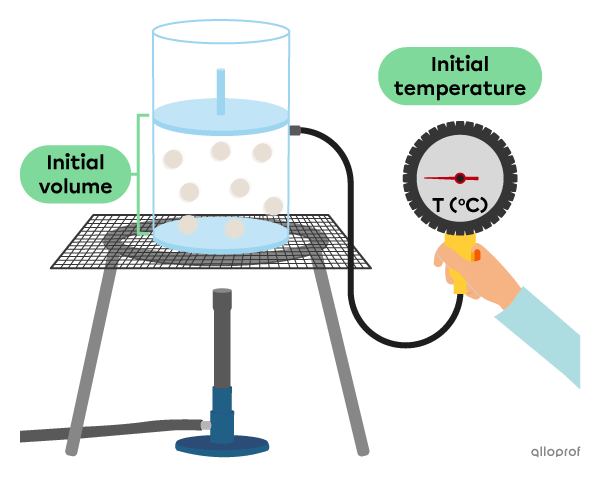
Before heating the gas, it has a certain volume.
When heating the gas, we can see its volume increase as a function of its temperature.
The data indicate a partial variation function.
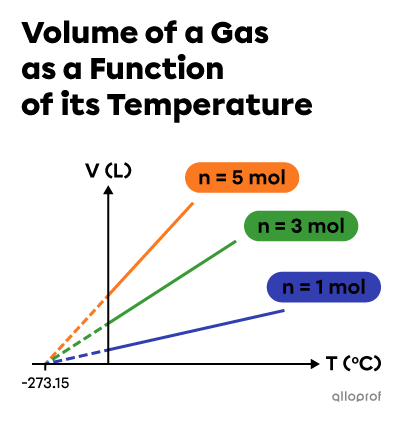
By carrying out the same experiment, but with different amounts of gas, we can see that the extrapolations of the lines all converge towards the same value for the x-coordinate at the origin. In 1848, the Irish born physicist Lord Kelvin set this value at |(-273{.}15 ^\circ\text{C}),| the absolute zero.
Using the absolute temperature scale, the relation between the volume and temperature of a gas when the quantity |(n)| and pressure |(P)| are constant is described by a direct variation function where the quotient |\dfrac{V}{T}| is constant.
The absolute temperature scale is a temperature measurement scale where the lowest temperature allowed corresponds to absolute zero |(-273{.}15 ^\circ\text{C}).| This is the theoretical temperature at which the kinetic energy of particles would be null. There are no negative values on this scale and the unit of measurement is the kelvin |(\text{K}).|
||0\ \text{K}=-273{.}15\ ^\circ\text{C}||
To go from a temperature expressed in degrees Celsius |(^\circ\text{C})| to a temperature expressed in kelvins |(\text{K}),| we use the following formula.
||T_{\text{K}}=T_{^\circ\text{C}}+273{.}15||
Charles’s law states that the volume of a gas is directly proportional to its absolute temperature when the number of moles and the pressure are constant. It is expressed by the following formula.
When |P| and |n| are constant:
|V\propto\ T| where |\dfrac{V}{T}=\text{constant}|
where
|V : | Volume often in litres |(\text{L})|
|T : | Absolute temperature in kelvins |(\text{K})|
Since the quotient |\dfrac{V}{T}| is constant, we can use the following formula to compare the initial and the final state of a gas.
||\dfrac{V_\text{1}}{T_\text{1}}=\dfrac{V_\text{2}}{T_\text{2}}||
where
|V_\text{1} : | Initial volume often in litres |(\text{L})|
|T_\text{1} : | Initial temperature in kelvins |(\text{K})|
|V_\text{2} : | Initial volume often in litres |(\text{L})|
|T_\text{2} : | Final temperature in kelvins |(\text{K})|
Charles’s law can also be explained using the kinetic theory of gases.
When a gas is heated, the kinetic energy of its particles increases. Since the motion of the particles is amplified, the gas expands and occupies a larger volume. So when the temperature of a gas increases, its volume increases. Inversely, when its temperature decreases, its volume decreases.
If a gas is confined in a container, increasing its temperature tends to increase the number and intensity of collisions between its particles and the walls of the container. In a container of fixed volume, this would increase the pressure of the gas. In a container of variable volume, the volume occupied by the gas increases as the kinetic energy of the particles increases, which allows the pressure to stay the same.
This means that if the temperature of a gas increases, its volume tends to increase proportionally when the amount of matter and the pressure are constant.
Simple gas laws apply only for ideal gases.
The values calculated using the simple gas laws correspond approximately to the real values, as long as the gas temperature is not too low and the pressure is not too high.
Rubber balloons are inflated in preparation for a birthday party. The balloons are inflated inside the house, at a temperature of |20{.}00\ ^\circ\text{C}.| Each balloon contains a volume of |1{.}50\ \text{L}| of air. Later in the day, the balloons are placed outside where the temperature is |33{.}00\ ^\circ\text{C}.| Knowing that the balloons have a maximum capacity of |1{.}80\ \text{L,}| are they at risk of popping?
See solution
See Also
- The Kinetic Theory of Gases
- Simple Gas Laws
- The Relationship Between Pressure and Temperature (Gay-Lussac’s Law)
- The Relationship Between Volume and Number of Moles (Avogadro’s Law)
- The Relationship Between Pressure and Number of Moles
- The General Gas Law
- The Ideal Gas Law
- The Law of Partial Pressures (Dalton’s Law)