Subjects
Grades
Demonstrations of UARM formulas
Concept sheet | Physics
Secondary
5
Table of contents
- Top of page
- Demonstration of the Formula |v_{f}=v_{i} + a \cdot {\triangle t}|
- Demonstration of the Formula |\triangle x= v_{i} \cdot \triangle t +\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}|
- Demonstration of the Formula |\triangle x= \displaystyle \frac{(v_{i} + v_{f}) \cdot {\triangle t}}{2}|
- Demonstration of the Formula |\triangle x= v_{f} \cdot \triangle t -\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}|
- Demonstration of the Formula |{v_{f}}^2={v_{i}}^2+2 \cdot a \cdot \triangle x|
The concepts covered in this concept sheet go beyond the normal secondary school curriculum. It is directed at students who are curious and want to learn more.
The formulas used in Uniformly Accelerated Rectilinear Motion (UARM) come from the graphical study of motion. To determine these relationships, a graph of speed as a function of time will be used.
| |v_{avg}=\displaystyle \frac{\triangle x}{\triangle t}| | |a=\displaystyle \frac{\triangle v}{\triangle t}| |
| |v_{f}=v_{i} + a \cdot {\triangle t}| | |\triangle x= v_{i} \cdot \triangle t +\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}| |
| |\triangle x= \displaystyle \frac{(v_{i} + v_{f}) \cdot {\triangle t}}{2}| | |\triangle x= v_{f} \cdot \triangle t -\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}| |
| |{v_{f}}^2={v_{i}}^2+2 \cdot a \cdot \triangle x| |
- Demonstration of the Formula |v_{f}=v_{i} + a \cdot {\triangle t}|
- Demonstration of the Formula |\triangle x= v_{i} \cdot \triangle t +\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}|
- Demonstration of the Formula |\triangle x= \displaystyle \frac{(v_{i} + v_{f}) \cdot {\triangle t}}{2}|
- Demonstration of the Formula |\triangle x= v_{f} \cdot \triangle t -\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}|
- Demonstration of the Formula |{v_{f}}^2={v_{i}}^2+2 \cdot a \cdot \triangle x|
The following formulas are derived from a graph of speed as a function of time (or speed versus time). The following graph indicates the different variables used in the following formulas.
Demonstration of the Formula |v_{f}=v_{i} + a \cdot {\triangle t}|
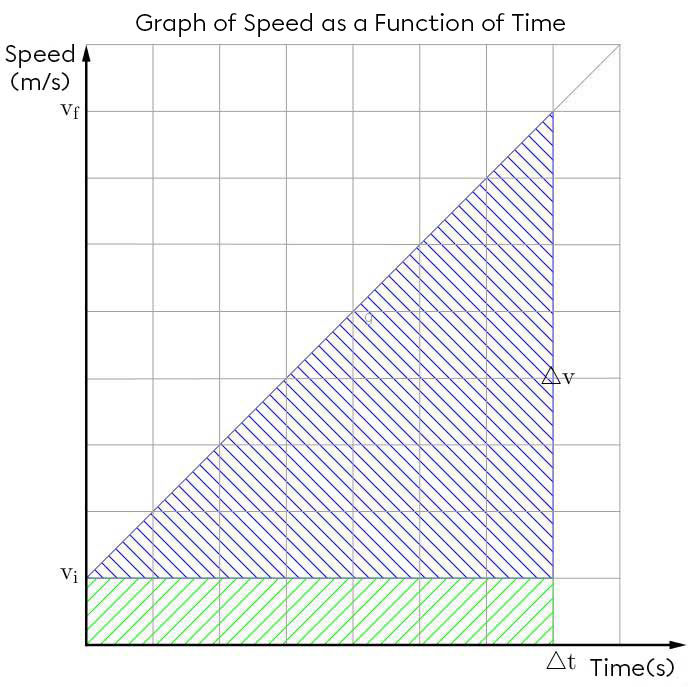
The definition of acceleration, or a speed change occurring over an interval of time, is the basic formula to use. ||a = \displaystyle \frac {\triangle v}{\triangle t}|| Using cross multiplication, it is possible to simplify the equation. ||{\triangle v}=a \cdot {\triangle t}|| A speed change is calculated by determining the difference between the final speed and the initial speed. ||{\triangle v} = v_f - v_i|| By substituting this formula in the previous step’s formula, we obtain a new formula. ||v_f - v_i=a \cdot {\triangle t}|| By isolating the final speed, we obtain the formula that had to be demonstrated. ||v_f = v_i + a \cdot {\triangle t}||
Demonstration of the Formula |\triangle x= v_{i} \cdot \triangle t +\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}|
In the graph above of speed as a function of time, we can calculate the displacement by calculating the area under the curve. In the graph, the area under the curve is represented by a green rectangle and a blue triangle. ||\triangle x=\text {Area}_{\text { green rectangle}} + \text {Area}_{\text { blue triangle}}|| To find the area of the green rectangle, multiply the base by the height. The base is represented by the time interval, while the height represents the initial speed. ||\text {Area}_{\text { green rectangle}} = v_i \cdot \triangle t|| To find the area of the blue triangle, multiply the base by the height and divide the result by two. For the triangle, the base represents the time interval and the height represents the change in speed.
||\text {Area}_{\text { blue triangle}} = \displaystyle \frac {\triangle v \cdot \triangle t}{2}|| By replacing the two area formulas in the starting formula, we obtain the following formula.
||\triangle x=v_i \cdot \triangle t + \displaystyle \frac {\triangle v \cdot \triangle t}{2}|| To simplify the formula, the speed change must be replaced. To do this, we will use the formula for acceleration.
||a = \displaystyle \frac {\triangle v}{\triangle t}|| Using cross multiplication, we simplify the expression to obtain the following formula.
||{\triangle v}=a \cdot {\triangle t}|| Thus, by substituting this formula in the previous formula, we obtain the following result.
||\triangle x=v_i \cdot \triangle t + \displaystyle \frac {a \cdot {\triangle t} \cdot \triangle t}{2}|| Finally, by grouping similar terms together, we obtain the formula to be demonstrated.||\triangle x= v_{i} \cdot \triangle t +\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}||
Demonstration of the Formula |\triangle x= \displaystyle \frac{(v_{i} + v_{f}) \cdot {\triangle t}}{2}|
In the graph above of speed as a function of time, we can calculate the displacement by calculating the area under the curve. In the graph, the area under the curve is represented by a trapezoid.||\triangle x=\text {Area}_{\text { trapezoid}}|| The formula used to calculate the area of a trapezoid is the following.
||\triangle x=\displaystyle \frac {(B + b) \cdot h}{2}|| By analyzing the graph, the large base represents the sum of the initial speed and the change in speed, the small base represents the initial speed and the height represents the height of the trapezoid.
||\triangle x=\displaystyle \frac {((v_i + \triangle v) + v_i) \cdot \triangle t}{2}|| However, a speed change is defined by the difference between the final speed and the initial speed.
||\triangle v=v_f-v_i|| By substituting this formula in the area of a trapezoid’s formula, we obtain the following result.
||\triangle x=\displaystyle \frac {((v_i + v_f-v_i) + v_i) \cdot \triangle t}{2}|| Finally, by simplifying, we obtain the formula to be demonstrated.||\triangle x=\displaystyle \frac {(v_f + v_i) \cdot \triangle t}{2}||
Demonstration of the Formula |\triangle x= v_{f} \cdot \triangle t -\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}|
In the graph above of speed as a function of time, we can calculate the displacement by calculating the area under the curve. In the graph, the area under the curve is represented by a green rectangle and a blue triangle.||\triangle x=\text {Area}_{\text { green rectangle}} + \text {aire}_{\text { blue triangle}}|| To find the area of the green rectangle, multiply the base by the height. However, the base is represented by the time interval, while the height represents the initial speed.||\text {Area}_{\text { green rectangle}} = v_i \cdot \triangle t|| To find the area of the blue triangle, multiply the base by the height and divide the result by two. For the triangle, the base represents the time interval and the height represents the change in speed.
||\text {Area}_{\text { blue triangle}} = \displaystyle \frac {\triangle v \cdot \triangle t}{2}|| By replacing the two area formulas in the starting formula, we obtain the following formula.
||\triangle x=v_i \cdot \triangle t + \displaystyle \frac {\triangle v \cdot \triangle t}{2}|| To simplify the formula, the speed change must be replaced. A speed change is defined by the difference between the final speed and the initial speed.
||\triangle v=v_f-v_i|| By substituting this formula in the previous step’s formula, we obtain the following expression.
||\triangle x=v_i \cdot \triangle t + \displaystyle \left( \frac {v_f-v_i} {2} \right)\cdot \triangle t|| To simplify the calculation, one carries out the distributive property of time.
||\triangle x=v_i \cdot \triangle t + \displaystyle \frac {v_f\cdot \triangle t}{2}-\frac{v_i \cdot \triangle t} {2}|| Since there are two similar terms, they are grouped together to simplify the expression.
||\triangle x=\displaystyle \frac{v_i \cdot \triangle t} {2} + \displaystyle \frac {v_f\cdot \triangle t}{2}|| By multiplying by two, we eliminate the fractions.
||2\cdot \triangle x= v_i \cdot \triangle t + v_f \cdot \triangle t|| Next, the first formula demonstrated in this concept sheet will be used.
||v_i = v_f - a \cdot {\triangle t}|| By substitution, we obtain the following formula.
||2\cdot \triangle x= (v_f - a \cdot \triangle t) \cdot \triangle t + v_f \cdot \triangle t||To simplify the calculation, carry out the distributive property of time.
||2\cdot \triangle x= v_f\cdot \triangle t - a \cdot \triangle t^2 + v_f \cdot \triangle t|| Since there are two similar terms, they are grouped together to simplify the expression.
||2\cdot \triangle x= 2 \cdot v_f\cdot \triangle t - a \cdot \triangle t^2|| By dividing each of the terms by two, we obtain the formula to be demonstrated.
||\triangle x= v_{f} \cdot \triangle t -\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}||
Demonstration of the Formula |{v_{f}}^2={v_{i}}^2+2 \cdot a \cdot \triangle x|
The definition of acceleration, or the speed change occurring over an interval of time, is the basic formula to use. ||a=\displaystyle \frac {\triangle v}{\triangle t} = \displaystyle \frac {v_f-v_i}{\triangle t}|| By cross multiplication, it is possible to rearrange the equation. ||\triangle t = \displaystyle \frac {v_f-v_i}{a}|| Next, it is necessary to use the third formula demonstrated in this concept sheet. ||\triangle x= \displaystyle \frac{(v_{i} + v_{f}) \cdot {\triangle t}}{2}|| By substituting this formula in the previous step’s formula, we obtain a new formula. ||\triangle x= \displaystyle \frac{(v_{i} + v_{f})}{2} \cdot \frac {(v_f-v_i)}{a}|| Multiplying the two fractions together gives us the following expression. ||\triangle x= \displaystyle \frac{(v_{i} + v_{f})\cdot (v_f-v_i)}{2 \cdot a}|| By distributing the terms in the numerator, we obtain the following expression. ||\triangle x= \displaystyle \frac{{(v_{f}}^2 - {v_{i}}^2)}{2\cdot a}|| By cross multiplication, we get the following result. ||2 \cdot a \cdot \triangle x={v_{f}}^2 - {v_{i}}^2|| By isolating the final speed, we obtain the expression to be demonstrated. ||{v_{f}}^2 = {v_{i}}^2 + 2 \cdot a \cdot \triangle x||