Subjects
Grades
Method for Observing Light Refraction
Concept sheet | Physics
Secondary
5
Table of contents
This concept sheet explains the steps to follow to find the refractive index of a substance.
Refraction is the phenomenon in which light deviates from its rectilinear path, changing speed when it passes from one transparent medium to another. The deflection is determined by the refractive index of a substance: the higher the refractive index, the more pronounced the deflection will be.
Equipment
-
Ray box
-
Semi-circular basin
-
Substance to be identified
-
Sheet of paper
-
Protractor
-
Ruler
Procedure
1. Draw two perpendicular lines crossing each other in the centre of the sheet of paper.
2. Position the semi-circular basin containing the substance to be identified, making sure that the centre of the basin is centred with the normal.
3. Draw the outline of the basin on your sheet.
4. Project a ray of light on the flat part of the semi-circular basin.
5. Using a dotted line, draw the incident ray and the refracted ray.
6. Identify the incident ray (I1) and the refracted ray (R1).
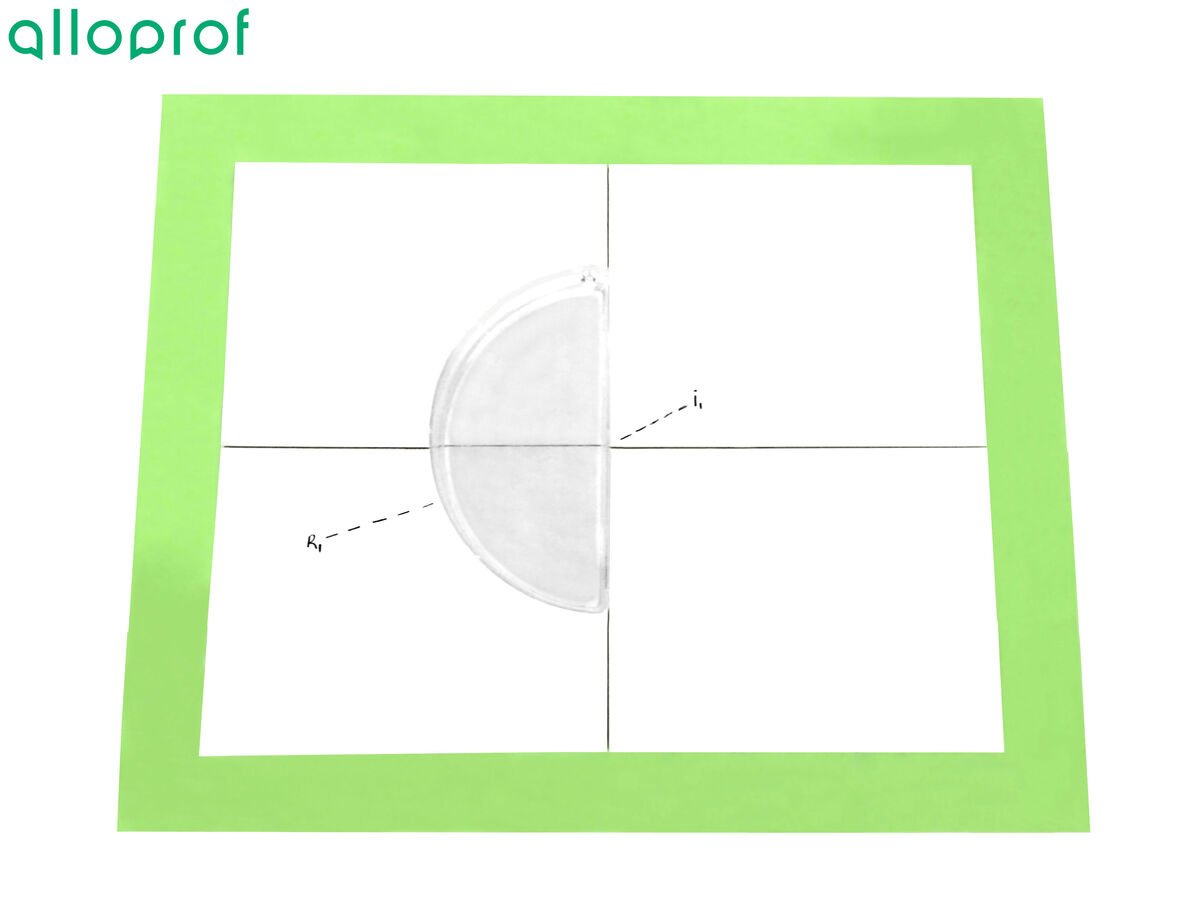
7. Repeat steps 5 and 6 to have three more angle measurements.
8. Remove the ray box and the semi-circular basin from the sheet of paper.
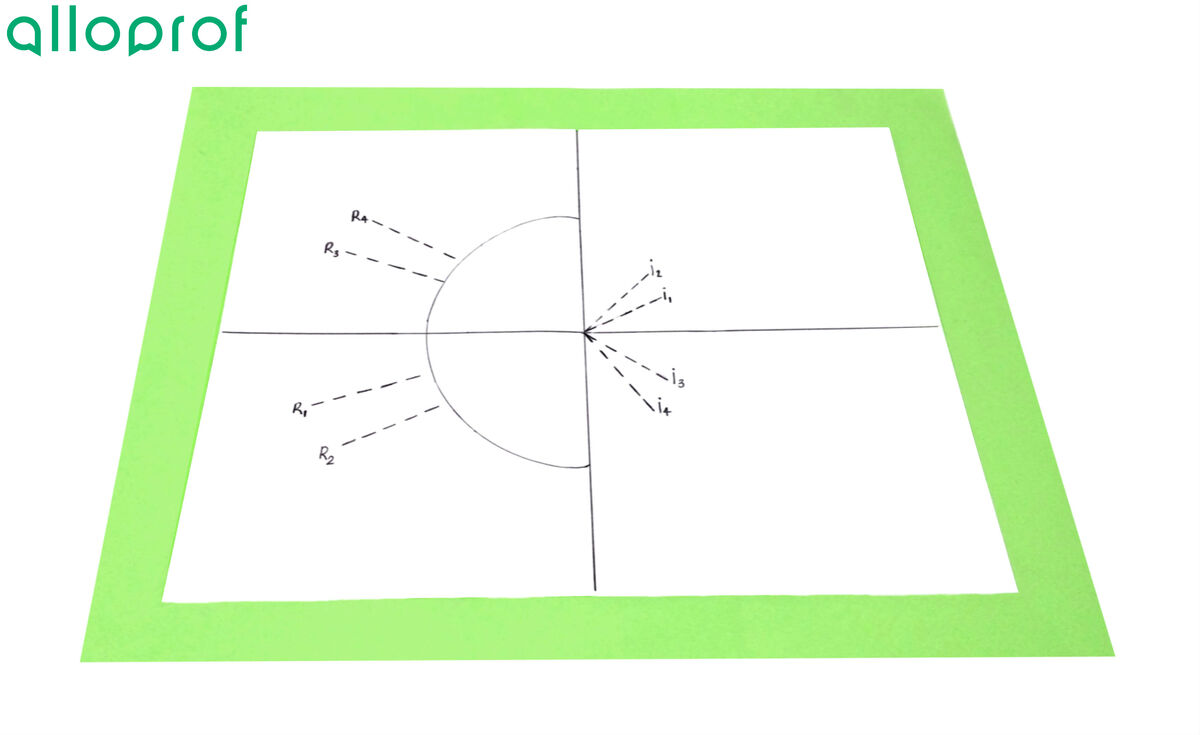
9. Draw a line for each of the incident rays to the centre of the basin.
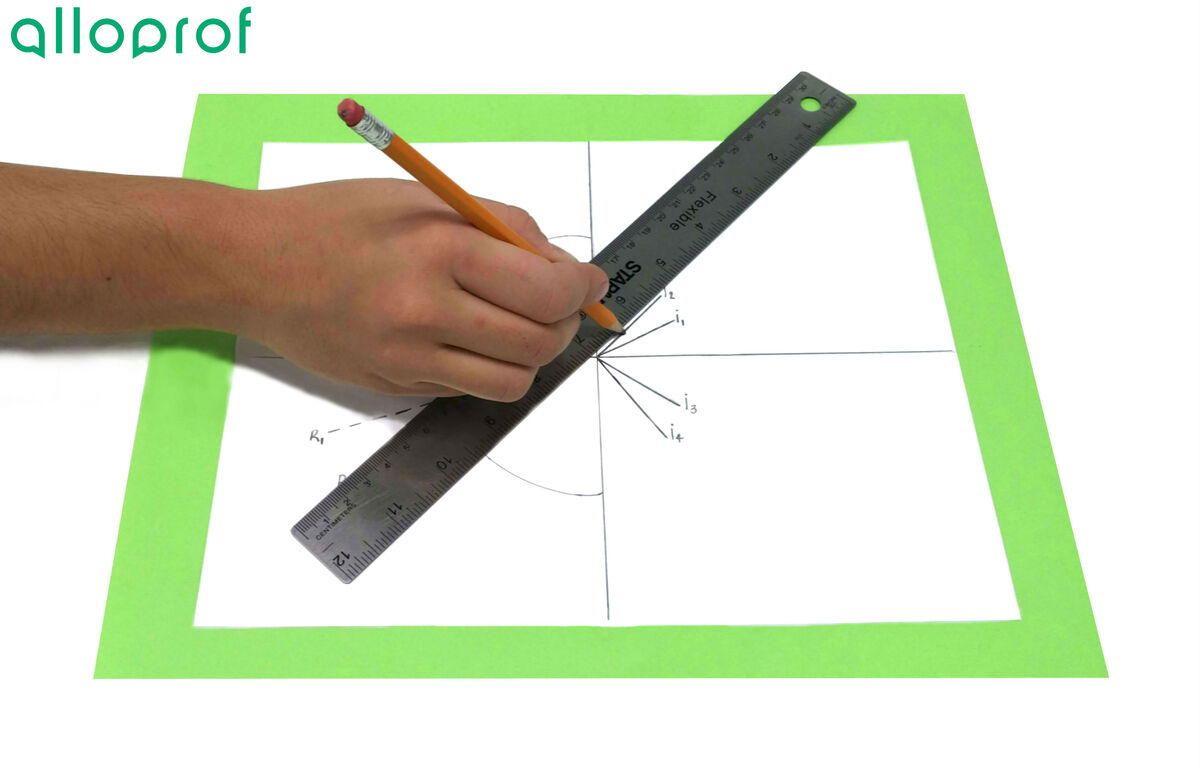
10. Draw a line running to the centre of the basin for each refracted ray.
11. Measure the angles of incidence and refraction of each ray with a protractor.
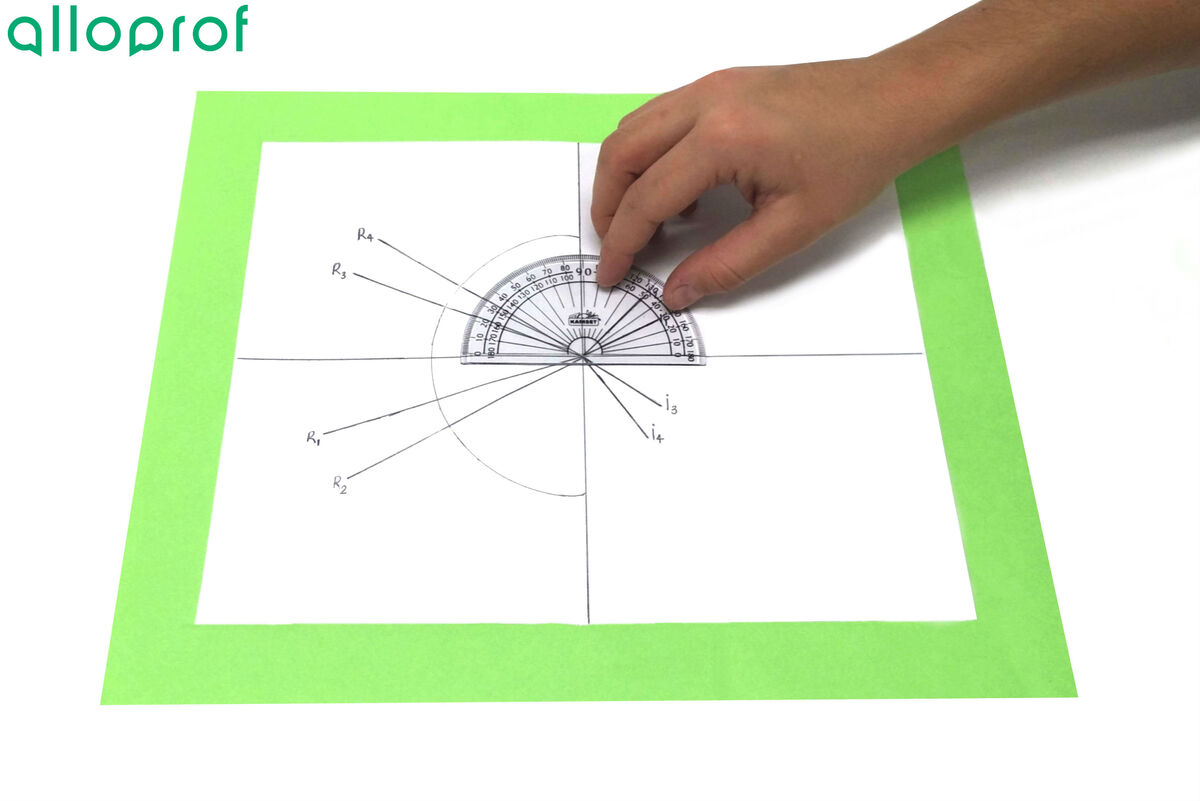
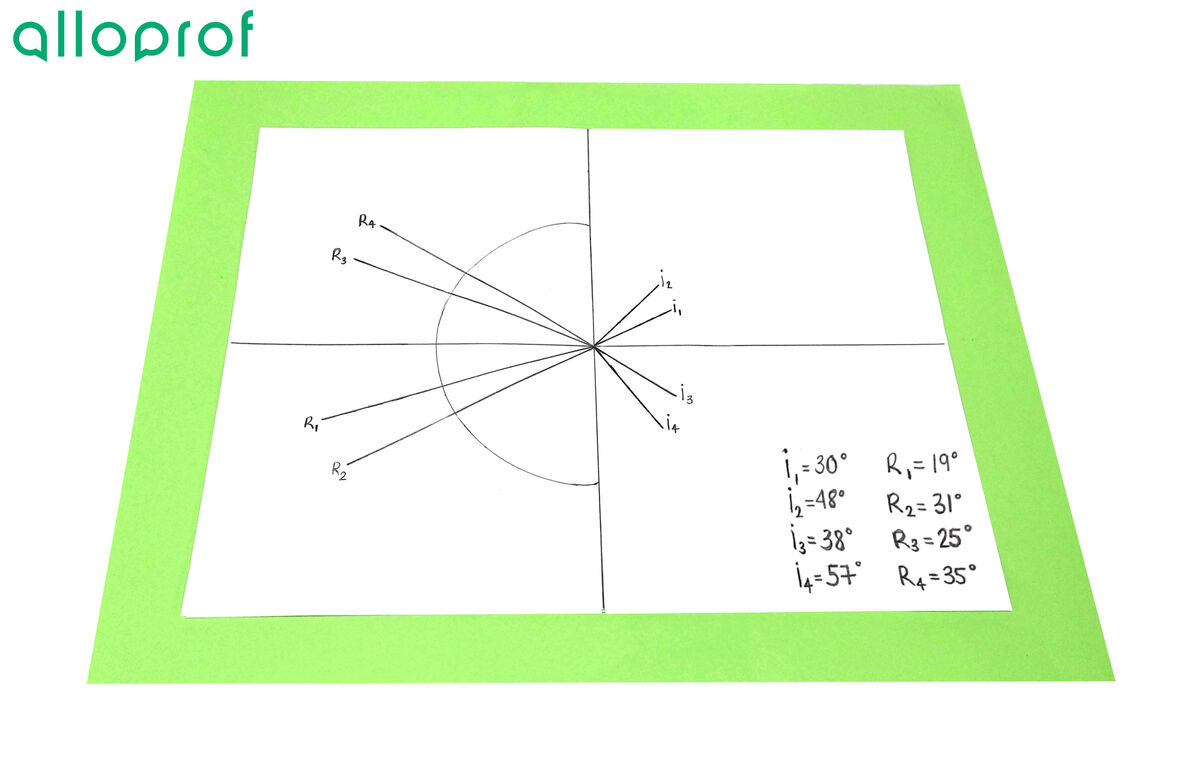
12. Calculate the refractive index for each measurement taken.
13. Clean and put away the equipment.
Results
Once the incident and refracted angles have been determined, it is possible to determine the refractive index of the substance to be identified using the Snell-Descartes law of refraction.
If the angle of incidence is |48.0^{\circ}| and the angle of refraction is |31.0^{\circ}|, what is the refractive index of the substance?
||\begin{align}n_{1} &= 1.00\ &\theta_{i} &= 48.0^{\circ}\\ n_{2} &= x&\theta_{r} &= 31.0^{\circ}\\ \end{align}||
The formula is used to determine the refractive index.
||\begin{align} n_{1} \times \sin \theta_{i} = n_{2}\times \sin\theta_{r} \quad \Rightarrow \quad n_{2} &= \left(
\frac {n_{1} \times \sin \theta_{i}}{\sin\theta_{r}} \right) \\ \\&= \left( \frac{1.00\times \sin 48.0^{\circ}}{\sin 31.0^{\circ}} \right) \\ \\ &= 1.44 \end{align}||
The refractive index is |1.44| for these measured angles of incidence and refraction.
The advantage of taking multiple measurements is that you can calculate an average of the results. It is, therefore, important to show all the results in a results table. The template below can be used to record the results.
Refractive index of an Unknown Substance Relative to Air
|
|
Angle of incidence |(^{\circ})| |
Refraction angle |(^{\circ})| |
Refractive index |
|
Trial #1 |
|30^{\circ}| |
|19^{\circ}| |
|1.54| |
|
Trial #2 |
|48^{\circ}| |
|31^{\circ}| |
|1.44| |
|
Trial #3 |
|38^{\circ}| |
|25^{\circ}| |
|1.46| |
|
Trial #4 |
|57^{\circ}| |
|35^{\circ}| |
|1.46| |
|
Average refractive index |
|1.475| |
||
It is possible to identify the unknown substance by comparing the value of the refractive index with the values listed in a reference table.