Subjects
Grades
Measuring Temperature
Concept sheet | Science and Technology
Secondary
1-2
Table of contents
This concept sheet explains the procedures for determining the temperature measurement of a substance.
Temperature measures the degree of agitation of particles in a substance. A thermometer must be used to measure it.
Thermometer
In the laboratory, temperature is usually measured with an alcohol thermometer. This instrument contains a liquid that expands under the effect of heat. Therefore, when the liquid inside the thermometer comes in contact with a body that is hot, it expands. The higher the temperature, the more the liquid expands. As a result, the liquid rises in the thermometer tube.
In order to get a proper thermometer reading, there are some important rules to follow.
- The thermometer bulb must be completely immersed in the solution in which the temperature is to be measured.
- Look down to the same level as the liquid inside the thermometer. If your eyes are placed higher or lower than the meniscus, the thermometer reading will be incorrect.
- To properly determine the temperature, find the scale of the thermometer. To do this, first count the number of graduations (number of spaces) between two divisions of the thermometer. The next step consists in finding the temperature difference between these two divisions. Finally, divide this volume by the number of graduations.
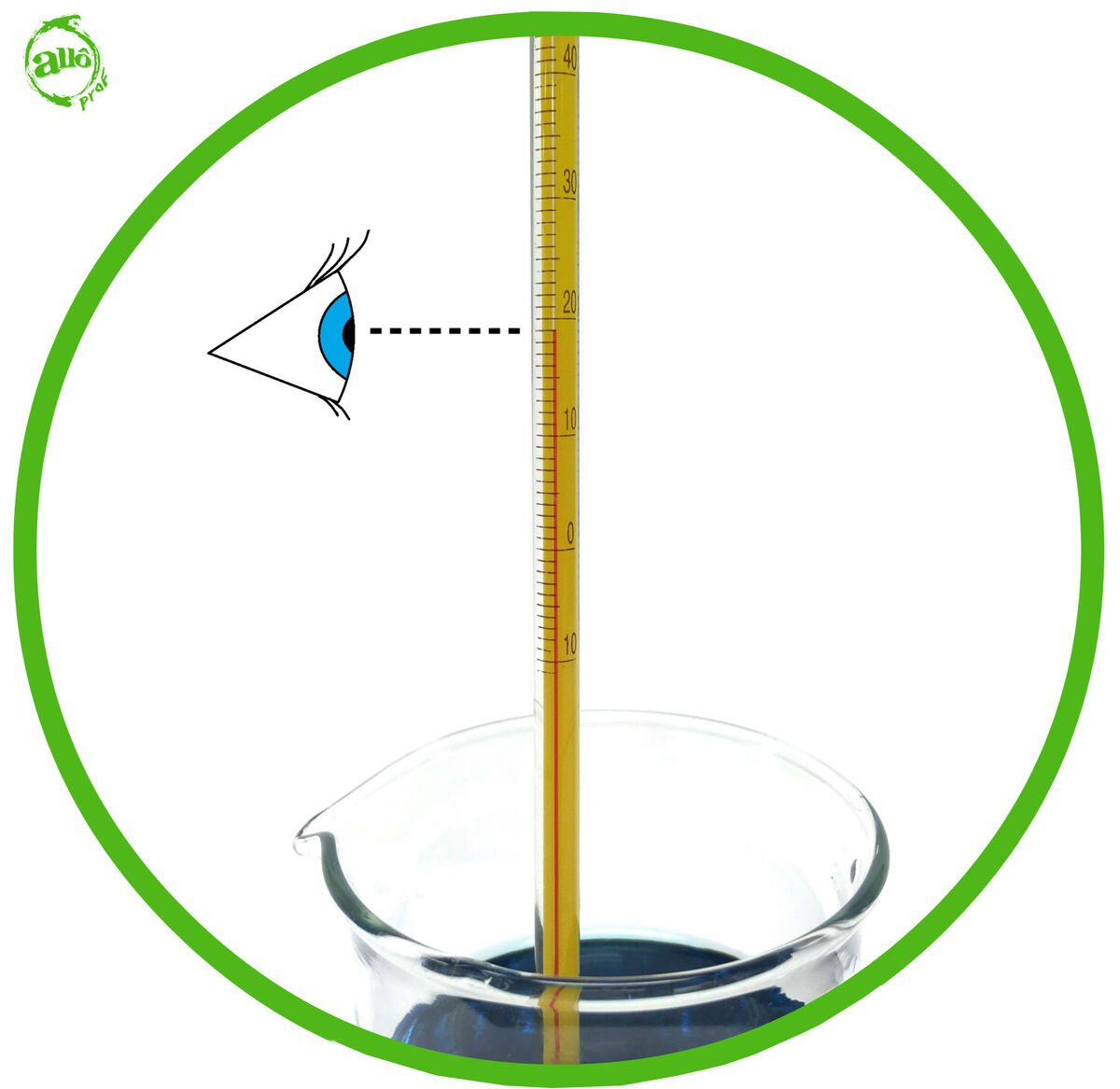
A thermometer has 10 graduations between |20 \: ^{\circ} \text{C}| and |30 \: ^{\circ} \text{C}| divisions.
The difference between the 2 divisions is |10 \: ^{\circ} \text{C}| |(30 \: ^{\circ} \text{C}-20 \: ^{\circ} \text{C} = 10 \: ^{\circ} \text{C})| .
The scale of this graduated cylinder is therefore |\displaystyle \frac {10 \: ^{\circ} \text{C}}{10 \: \text{graduations}}=1 \: ^{\circ} \text{C} |.
- The final step simply consists in taking the thermometer reading.
The temperature is therefore |19 \: ^{\circ} \text{C}| .
Since different models of thermometers exist, it is best to calculate the scale each time a thermometer is used.
Furthermore, when using an alcohol thermometer, it is important to follow certain safety rules.
- Handle the thermometer with care; it can easily be broken since it is made of glass.
- Hold the thermometer in the middle and not by the bulb.
- Never use a thermometer as a stirrer.
Temperature Measurement
The method used to measure temperature is similar regardless of the material state of matter of the object to measure.
1. Place the thermometer bulb in contact with the substance of which the temperature is to be measured.
2. Wait for the liquid level inside the thermometer to stabilize.
3. Take the temperature reading on the thermometer.
In the lab, temperature is usually measured in degrees Celsius. However, temperatures may also be measured in degrees Fahrenheit.
To convert degrees Celsius to degrees Fahrenheit:
|T(^{\circ} \text{F}) = T(^{\circ} \text{C}) \times 1.8 + 32|
To convert degrees Fahrenheit to degrees Celsius:
|T(^{\circ} \text{C}) = \displaystyle \frac {(T(^{\circ} \text{F}) - 32)}{1.8}|