Matières
Niveaux
L'accélération
Fiche | Physique
Secondaire
5
L'accélération est le rapport entre le changement de vitesse d'un mobile et le temps nécessaire pour effectuer ce changement de vitesse.
Lorsqu'une voiture se met à rouler après avoir fait un arrêt à un feu de signalisation, sa vitesse augmente: elle accélère. De plus, si cette même voiture freine pour s'arrêter à un panneau d'arrêt, sa vitesse diminue: son accélération est négative. Dans le langage courant, on dit que la voiture décélère.
L'équation générale utilisée pour calculer l'accélération d'un mobile est:
|a=\displaystyle \frac{\triangle v}{\triangle t}|
où
|a| représente l'accélération du mobile |\text {(en m/s}^2)|
|\triangle v| représente la variation de la vitesse du mobile |\left( v_{f} - v_{i} \right)| |\text {(en m/s)}|
|\triangle t| représente la variation de temps |\left( t_{f} - t_{i} \right)| |\text {(en s)}|
La formule ci-dessus revient à calculer la pente d'une droite dans un graphique. En effet, en présence d'un graphique de la vitesse d'un mobile en fonction du temps, le calcul de la pente de ce graphique permet de déterminer l'accélération du mobile.
Les unités de mesure de l'accélération sont des mètres par seconde carré |\small \text {(m/s}^2)|. Ces unités sont établies à partir de la formule de l'accélération.
||\begin{align} a = \displaystyle \frac {\triangle v}{\triangle t} \quad \Rightarrow \quad
a &= \displaystyle \frac {\text {m/s}}{\text {s}} \\
&= \displaystyle \frac {\text {m}}{\text {s}} \times \frac {1}{\text {s}} \\
&= \displaystyle \frac {\text {m}}{\text {s}^{2}} \end{align}||
L'erreur souvent observée est d'annuler les unités de temps dans le calcul: elles sont toutefois très importantes puisque l'accélération représente un changement de vitesse durant une période de temps.
D'un point de vue graphique, deux relations peuvent être obtenues:
| Si le graphique de l'accélération en fonction du temps donne une fonction de variation nulle qui n'est pas superposée à l'axe des abscisses, le mobile accélère (si la droite est au-dessus de l'axe des x) ou décélère (si la droite est en dessous de l'axe des x). | Si le graphique de l'accélération en fonction du temps donne une fonction de variation nulle superposée à l'axe des x, le mobile se déplace à vitesse constante sans qu'il accélère. Ceci peut également signifier que le mobile n'est pas en mouvement. |
 |
 |
Comme pour la vitesse, il existe deux types d'accélération:
- L'accélération moyenne, qui détermine le changement de vitesse durant un intervalle de temps prédéterminé;
- L'accélération instantanée, qui détermine l'accélération à un moment précis.
Une voiture arrêtée à un panneau de signalisation accélère après avoir fait son arrêt obligatoire. On représente dans un graphique sa vitesse en fonction du temps. Quelle est l'accélération moyenne de la voiture durant les cinq premières secondes de son déplacement?
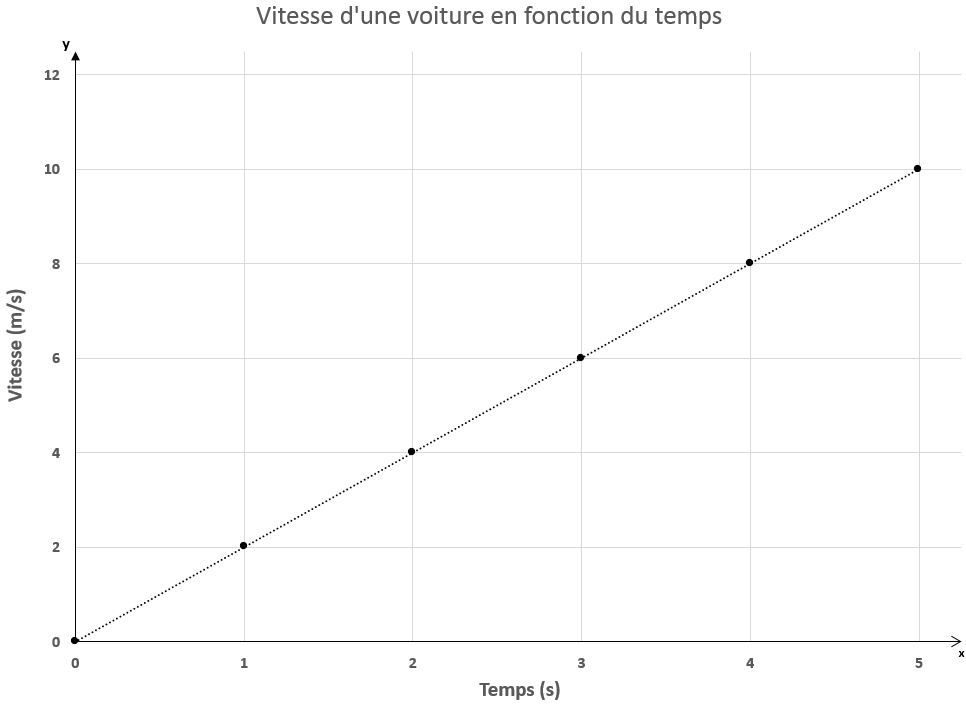
Pour déterminer l'accélération, il faut déterminer la variation de la vitesse et la variation de temps. Il est mentionné dans la question que la variation de temps est de cinq secondes. En observant le graphique, le dernier point indique qu'après cinq secondes, la voiture se déplaçait à une vitesse de |\small \text {10 m/s}|. En utilisant la formule de l'accélération, on obtient donc:
||\begin{align} a = \displaystyle \frac {\triangle v}{\triangle t} \quad \Rightarrow \quad
a &= \displaystyle \frac {\text {10 m/s}}{\text {5 s}} \\
&= {\text {2 m/s}^2} \end{align}||
La voiture a donc accéléré de |\text {2 m/s}^2|. Une accélération positive signifie que la voiture augmentait sa vitesse dans le même sens que le mouvement de la voiture.
Graphique de l'accélération en fonction du temps
Le graphique de l'accélération en fonction du temps nous informe du changement de vitesse d’un objet à tout moment.
- Durant les deux premières secondes, l'objet accélère positivement. Ceci signifie que sa vitesse augmente de plus en plus. On ne sait rien sur la direction de l'objet, car ce dernier pourrait avoir une vitesse négative et une accélération positive.
- L'objet cesse d'accélérer. L'objet peut être soit immobile, soit à vitesse constante: cette information ne peut pas être déterminée uniquement à partir du graphique d'accélération.
- Durant le troisième segment, l’objet a une accélération de |\small \text {-4 m/s}^2|. Une accélération négative représente un objet qui change de vitesse dans le sens contraire à l’orientation de référence. La vitesse diminuera (si elle était positive) ou elle augmentera (si elle était négative au début de ce segment).
- L'objet cesse d'accélérer. Tout comme au segment 2, l'objet peut être soit immobile, soit à vitesse constante.
- L'objet accélère. Sa vitesse augmente si elle était positive au départ. Si la vitesse initiale était négative au départ, elle se rapprochera de |\small \text {0 m/s}| pour éventuellement la dépasser (selon la situation).
Déterminer la variation de vitesse (l’aire sous la courbe)
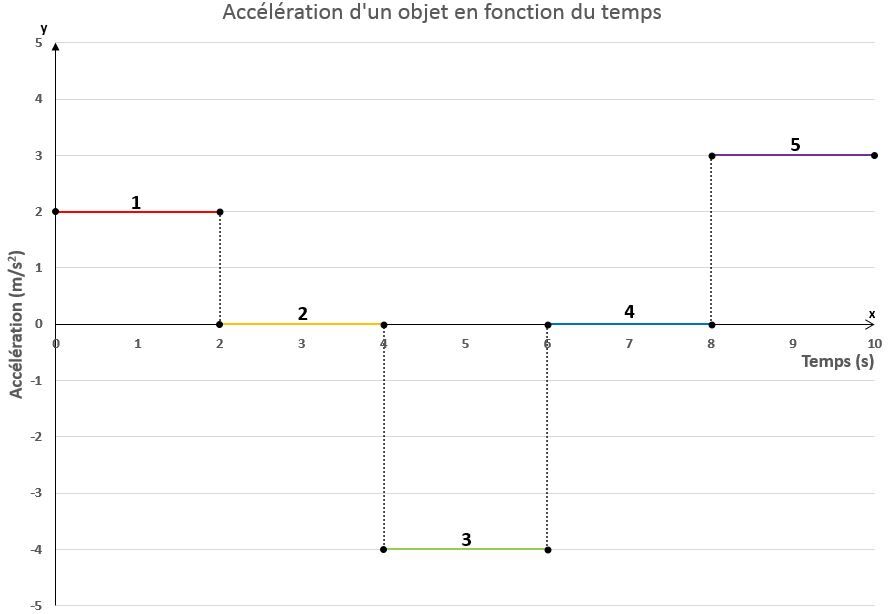
Dans un graphique de l'accélération en fonction du temps, l’aire sous la courbe indique la variation de vitesse que l'objet subira à l’intérieur d'un intervalle de temps.
Calcule la variation de vitesse que subit l'objet entre la huitième et la dixième seconde.
Voir la solution
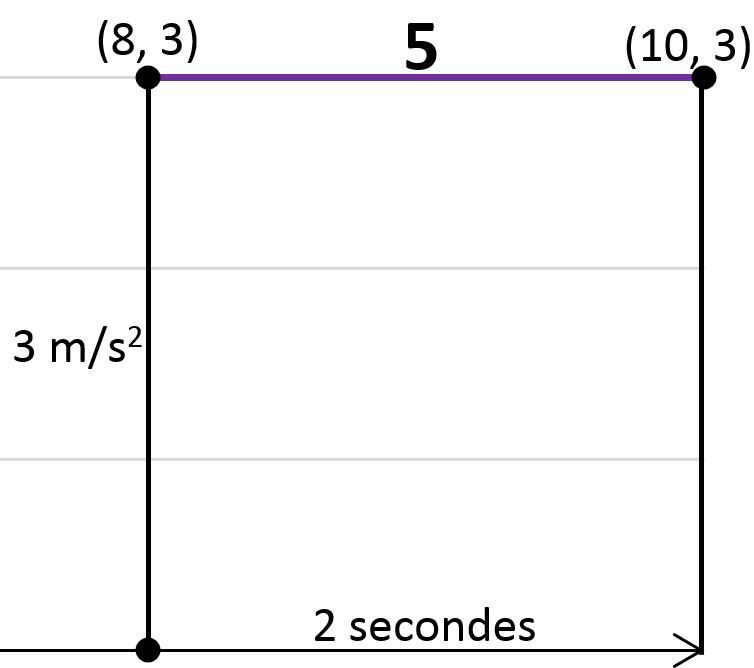
Lorsque l’aire sous la courbe représente une zone sous l’axe des x, on calculera un changement de vitesse négatif. Cette valeur négative est logique, puisque sous l’axe des x, l'accélération est négative. Ceci signifie que la vitesse diminue (si elle était plus grande que zéro au départ) ou que la vitesse augmente, mais dans le sens contraire au système de référence.