Matières
Niveaux
La fiabilité des instruments de mesure
Fiche | Physique
Secondaire
5
La fiabilité des instruments de mesure permet de déterminer à quel point une mesure obtenue par un appareil donne un résultat qui est précis et qui peut être répété à un autre moment par une autre personne qui obtiendra, à son tour, un résultat semblable.
Théoriquement, deux personnes qui effectuent le même laboratoire dans des conditions semblables devraient obtenir des résultats identiques. Toutefois, lorsque vient le temps de prendre des données en laboratoire, deux types d'erreurs peuvent survenir.
- Les erreurs aléatoires: Ce sont les erreurs constatées lorsqu'un grand nombre de mesures sont prises. Ces erreurs peuvent être causées par la personne qui fait les manipulations ou par le changement dans la mesure à prendre (comme, par exemple, si on tentait de mesurer la vitesse du vent).
- Les erreurs systématiques: Ce sont les erreurs liées à l'appareil de mesure qui peuvent être corrigés par un réglage approprié de l'instrument de mesure. Ce type d'erreur affectera toujours de la même façon les résultats. Plus l'erreur systématique est petite, plus les résultats seront précis.
Cette fiche vise principalement à évaluer l'effet de l'instrument de mesure sur la qualité des résultats. On évalue la fiabilité des instruments de mesure en fonction de quatre paramètres.
| La précision | Un instrument de mesure est précis si l'écart entre deux graduations est petit. |
| La fidélité | Un instrument de mesure est fidèle s'il est en mesure de donner le même résultat pour la même mesure dans des conditions semblables. |
| La sensibilité | Un instrument de mesure est sensible si les variations entre les différentes mesures sont grandes. |
| La justesse | Un instrument de mesure est juste lorsqu'il permet de prendre des mesures avec très peu d'erreurs. |
La précision
Un instrument de mesure est précis si l'écart entre deux graduations est petit.
L'incertitude absolue peut permettre de déterminer quel instrument est plus précis. Pour déterminer l'incertitude absolue d'un appareil non électronique ou non numérique, il faut prendre la moitié de la plus petite graduation, alors que l'incertitude absolue d'un appareil numérique ou électronique correspond à la plus petite graduation affichée.
Un appareil précis possèdera la plus petite incertitude absolue.
Pour mesurer un volume de |\small \text {20,0 ml}| d'eau, il est préférable d'utiliser un cylindre gradué de |\small \text {25,0 ml}|, qui possède une incertitude de |\small \pm \text {0,3 ml}|, plutôt qu'un cylindre gradué de |\small \text {50,0 ml}|, qui possède une incertitude de |\small \pm \text {0,4 ml}|, car le premier instrument est plus précis que le deuxième.
De manière générale, il est préférable d'utiliser l'incertitude relative comme mesure définitive de la précision. Plus l'incertitude relative est petite, plus la précision de la mesure est grande.
En laboratoire, les distances suivantes ont été mesurées: |\small \left( 100 \pm 2 \right) \: \text {cm}| et |\small \left( 10 \pm 1 \right) \: \text {cm}|. Laquelle de ces deux mesures est la plus précise ?
Pour la première mesure:
||\begin{align} \text {I.R.} = \frac{\text {Incertitude absolue}}{\text {Valeur mesurée}}\times \text {100} \quad \Rightarrow \quad \text {I.R.} &=
\frac {2 \: \text {cm}}{100 \: \text {cm}}\times \text {100} \\ \\
&= 2 \: \% \end{align}||
Pour la deuxième mesure:
||\begin{align} \text {I.R.} = \frac{\text {Incertitude absolue}}{\text {Valeur mesurée}}\times \text {100} \quad \Rightarrow \quad \text {I.R.} &=
\frac {1 \: \text {cm}}{10 \: \text {cm}}\times \text {100} \\ \\
&= 10 \: \% \end{align}||
La première mesure est donc plus précise, bien que son incertitude absolue soit plus grande.
La fidélité
Un instrument de mesure est fidèle s'il est en mesure de donner le même résultat pour la même mesure dans des conditions semblables.
La fidélité est déterminée par la dispersion (ou l'étendue) des résultats. Si on effectue plusieurs mesures pour un même objet, il faut s'attendre à ce que les résultats soient tous semblables. Toutefois, si des variations importantes devaient survenir entre ces mesures, on pourrait douter de la fidélité des mesures prises.
La fidélité peut s'étudier selon deux composantes.
- La répétabilité est la capacité d'une personne à répéter la même mesure dans le même local avec les mêmes instruments et dans les mêmes conditions.
Un élève dans un laboratoire de physique trouve que le temps de chute d'une balle à partir d'une hauteur d'un mètre est de |\small \left( 0,45 \pm 0,01 \right) \: \text {s}|. Il reprend ses mesures quelques minutes plus tard, et obtient des mesures de |\small \left( 0,45 \pm 0,01 \right) \: \text {s}| et |\small \left( 0,46 \pm 0,01 \right) \: \text {s}|. Il pourra mentionner que la répétabilité est bonne, car les mesures sont semblables lors des trois essais.
- La reproductibilité est la capacité d'un instrument de mesure à répéter la même mesure dans la même pièce, dans les mêmes conditions et ce, peu importe son utilisateur.
Un élève utilise une balance électronique et obtient une masse de |\small \left( 39,56 \pm 0,01 \right) \: \text {g}|. Quelques minutes plus tard, son coéquipier retourne peser le même objet, sur la même balance au même endroit. Il obtient une mesure de |\small \left( 40,41 \pm 0,01 \right) \: \text {g}|. On peut donc dire que la reproductibilité de l'instrument est très faible.
La sensibilité
Un instrument de mesure est sensible si les variations entre les différentes mesures sont grandes.
Un appareil est très sensible si une petite variation d'un paramètre entraîne un grand changement sur la mesure indiquée par l'instrument de mesure.
Pour un appareil possédant des graduations, on dira qu'il est sensible s'il possède des graduations très espacées les unes des autres, puisqu'il est plus facile d'effectuer une mesure avec ce genre d'instrument.
Les appareils numériques ou électroniques ont, de manière générale, une sensibilité plus élevée que les autres types d'appareils, comme les appareils analogiques.
La justesse
Un instrument de mesure est juste lorsqu'il permet de prendre des mesures avec très peu d'erreurs.
Une erreur de justesse est une erreur globale qui englobe toutes les causes d'erreurs pour chacun des résultats de mesure pris individuellement.
On peut calculer la justesse d'une mesure en déterminant la moyenne des mesures prises expérimentalement, puis en calculant la différence entre cette moyenne et la valeur théorique (ou la valeur attendue). Une différence très petite signifie que les mesures prises en laboratoire sont justes.
Un premier élève détermine que l'accélération gravitationnelle obtenue par la chute d'une balle est |\small 9,73 \: \text {m/s}^2| après avoir effectué cinq essais. Un autre élève de son groupe fait la même expérience et calcule l'accélération gravitationnelle comme étant |\small 9,89 \: \text {m/s}^2|. Le premier élève a obtenu une valeur plus juste, car l'écart à la valeur attendue, |\small 9,8 \: \text {m/s}^2|, est plus petit pour ses résultats (un écart de |\small 0,07 \: \text {m/s}^2| que l'écart à la valeur attendue pour le deuxième élève |\small 0,09\: \text {m/s}^2|.
La représentation de la fidélité et de la justesse
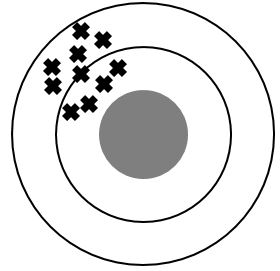
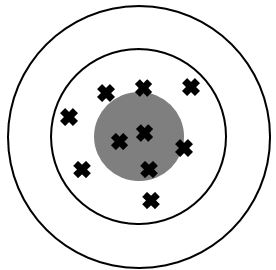
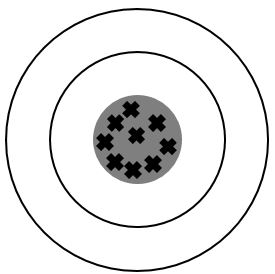
Les images suivantes représentent des situations qui évaluent la fidélité et la justesse de mesures. On peut imaginer les images comme si elles provenaient d'une personne qui lançait des dards sur une cible.
Un résultat juste est près de la valeur attendue.
Un résultat fidèle possède une petite dispersion (les résultats sont rapprochés les uns des autres).
 |
 |
|
Résultats infidèles
Résultats pas justes
Présence d'erreurs aléatoire et systématique
|
Résultats fidèles
Résultats pas justes
Présence d'erreurs systématiques |
 |
 |
|
Résultats infidèles
Résultats justes
Présence d'erreurs aléatoires |
Résultats fidèles
Résultats justes
Erreurs faibles
|