Matières
Niveaux
L'énergie potentielle gravitationnelle et l'énergie cinétique
Fiche | Sciences et technologies
Secondaire
4
Lorsqu’un objet se met en mouvement, il transfère ou transforme son énergie. Il peut, par exemple, convertir son énergie potentielle en énergie cinétique ou vice versa.
Même lorsqu’elle est transformée, l’énergie totale d’un objet est constante tout au long de son mouvement. La loi de la conservation de l’énergie s’applique en tout temps, peu importe le mouvement.
L’énergie mécanique correspond à la somme de l’énergie potentielle et de l’énergie cinétique. La notion d’énergie mécanique est abordée en physique de 5e secondaire.
L’énergie potentielle gravitationnelle
-
L’énergie potentielle est l’énergie emmagasinée par un objet en raison de sa position ou de sa forme.
-
L’énergie potentielle gravitationnelle |(E_{pg})| est l’énergie emmagasinée par un objet selon sa position par rapport au sol.
L’énergie potentielle gravitationnelle d’un objet varie proportionnellement selon :
-
sa masse;
-
sa hauteur par rapport au sol;
-
l’intensité du champ gravitationnel de l’astre par lequel il est attiré.
Un melon d’eau et une pomme se trouvent sur une table. L’énergie potentielle gravitationnelle du melon d’eau est plus élevée que celle de la pomme, car sa masse est plus grande.
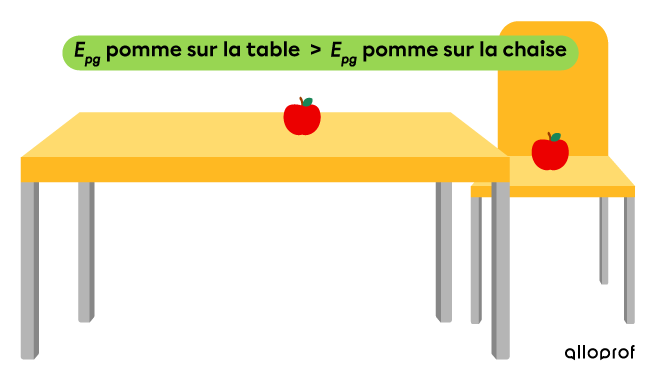
Une pomme se trouve sur une table et une autre pomme, sur une chaise plus basse. L’énergie potentielle gravitationnelle de la pomme sur la table est plus élevée que celle de la pomme sur la chaise, car sa hauteur par rapport au sol est plus grande.
Pour calculer l’énergie potentielle gravitationnelle, on utilise la formule qui suit.
|E_{pg}=mgh|
où
|E_{pg}| représente l’énergie potentielle gravitationnelle en joules |(\text{J})|
|m| représente la masse en kilogrammes |(\text{kg})|
|g| représente l’intensité du champ gravitationnel en newtons par kilogramme |(\text{N/kg})|
|g_{Terre}=9{,}81\ \text{N/kg}|
|h| représente la hauteur par rapport au sol en mètres |(\text{m})|
-
Il ne faut pas oublier de convertir l’unité de masse en |\text{kg}| lorsque nécessaire. Dans ce cas, on utilise la conversion suivante.
||1\ \text{kg} = 1\ 000\ \text{g}||
Ex. : |500\ \cancel{\text{g}} \times \dfrac{1\ \text{kg}}{1\ 000\ \cancel{\text{g}}} = 0{,}500\ \text{kg}| -
On utilise généralement la valeur de l'intensité du champ gravitationnel (g) de la Terre, soit |g_{Terre}=9{,}81\ \text{N/kg}|. Si la situation se déroule sur un autre astre, on utilisera la valeur de g de l'astre en question.
-
Certains manuels scolaires utilisent la variable |\Delta y| en remplacement de |h|. Le |\Delta y| représente une variation de la position verticale (selon l’axe des |y|) par rapport à un point de référence. On peut privilégier |\Delta y| lorsque le point de référence n’est pas le sol |(0\ \text{m})|. Dans ce cas, on utilise la formule suivante.
||\Delta y = y_{\text{f}}-y_{\text{i}}||
où
|y_{\text{f}}| représente la position finale selon l’axe des |y|
|y_{\text{i}}| représente la position initiale selon l’axe des |y|
Le 14 octobre 2012, Felix Baumgartner, un parachutiste et sauteur extrême, s’est élancé à partir d’une nacelle au niveau de la stratosphère à |38\ 969\ \text{m}| d’altitude.
Si on estime que Felix Baumgartner avait une masse de |65{,}0\ \text{kg}|, quelle était son énergie potentielle gravitationnelle juste avant de sauter?
La nacelle Stratos
Red Bull a conçu la nacelle Stratos qui a permis l’ascension de Felix Baumgartner jusqu’à la stratosphère avant son saut en chute libre.
Zinemo, Shutterstock.com
Voir la solution
L’énergie cinétique
L’énergie cinétique |(E_k)| est l’énergie d’un objet en raison de son mouvement.
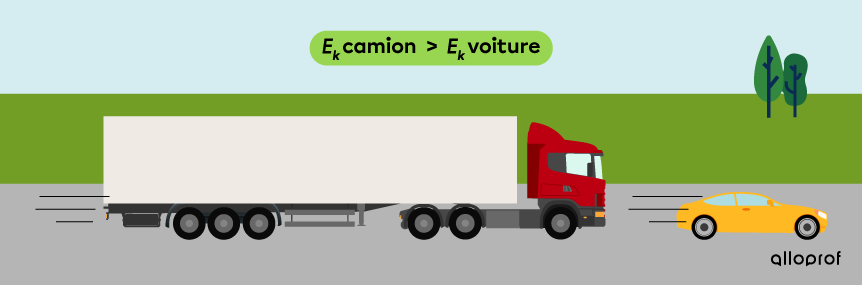
Un camion et une voiture roulent à la même vitesse. L’énergie cinétique du camion est plus élevée que celle de la voiture, car sa masse est plus grande.
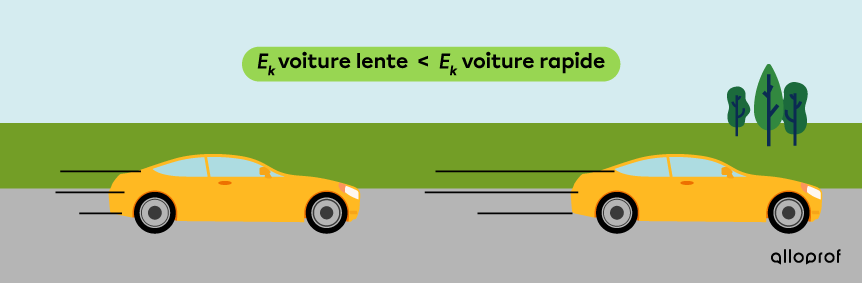
Deux voitures identiques roulent à des vitesses différentes. L’énergie cinétique de la voiture rapide est plus élevée que celle de la voiture lente, car sa vitesse est plus grande.
Pour calculer l’énergie cinétique, on utilise la formule qui suit.
|E_k = \dfrac{1}{2}mv^2|
où
|E_k| représente l’énergie cinétique en joules |(\text{J})|
|m| représente la masse en kilogrammes |(\text{kg})|
|v| représente la vitesse en mètres par seconde |(\text{m/s})|
-
Il ne faut pas oublier de convertir l’unité de masse lorsque nécessaire. Dans ce cas, on utilise la conversion suivante.
||1\ \text{kg}= 1\ 000\ \text{g}||
Ex. : |500\ \cancel{\text{g}} \times \dfrac{1\ \text{kg}}{1\ 000\ \cancel{\text{g}}} = 0{,}500\ \text{kg}| -
Il ne faut pas oublier de convertir l’unité de vitesse en m/s lorsque nécessaire. Dans ce cas, on utilise la conversion suivante.
||3{,}6\ \text{km/h}=1\ \text{m/s}|| puisque
||\dfrac {3{,}6\ \text{km}}{h}=\dfrac {1\ \cancel{\text{m}}}{\cancel{\text{s}}} \times\dfrac{3\ 600\ \cancel{\text{s}}}{\text{h}} \times \dfrac{1\ \text{km}}{1\ 000\ \cancel{\text{m}}}||
Ex. : |100\ \cancel{\text{km/h}} \times \dfrac{1\ \text{m/s}}{3{,}6\ \cancel{\text{km/h}}}=27{,}8\ \text{m/s}|
Lorsque Felix Baumgartner a sauté de la stratosphère, il a atteint une vitesse maximale de |1\ 342\ \text{km/h}|.
Si on estime que Felix Baumgartner avait une masse de |65{,}0\ \text{kg}|, quelle était son énergie cinétique au moment où il a atteint sa vitesse maximale?
Voir la solution
La transformation de l’énergie lors d’un mouvement de pendule
Selon la loi de la conservation de l’énergie, on sait que l’énergie ne peut qu’être transférée ou transformée. Dans notre quotidien, plusieurs phénomènes permettent de constater et de vérifier cette loi. Dans un mouvement de chute libre ou dans un mouvement d’oscillation, l’énergie potentielle d’un objet est progressivement transformée en énergie cinétique ou vice versa. Ainsi, l’objet ne subit aucune perte d’énergie.
Dans les exemples suivants, la hauteur et la vitesse des objets varient. Cette variation fait en sorte que l’énergie potentielle de l’objet (relative à sa hauteur) est convertie en énergie cinétique (relative à sa vitesse). Cette transformation se déroule en alternance puisque l’énergie est toujours conservée, elle est simplement transformée.
Le pendule d’une horloge
Mulevich, Shutterstock.com
Le rebond d’une balle de tennis
Raul Jichici, Shutterstock.com
Un planchiste sur une rampe demi-lune
Nick_p1cn1c, Shutterstock.com
Un gymnaste à la barre fixe
Alex Kravtsov, Shutterstock.com
Analyse de la transformation de l'énergie d’un pendule
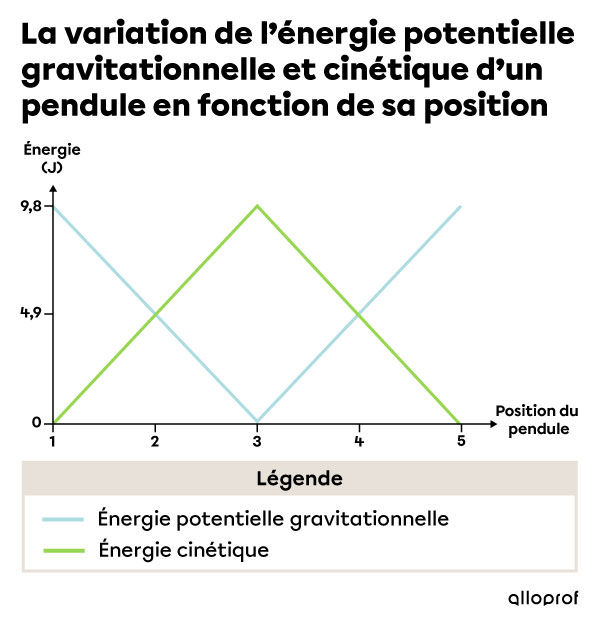
Le mouvement d’un pendule de |1{,}0\ \text{kg}| démontre la variation d’énergie potentielle gravitationnelle et cinétique lorsque la position et la vitesse du pendule changent.
Le pendule est d’abord immobile à la position 1, à une hauteur de |1{,}0\ \text{m}| par rapport au sol. Ensuite, le pendule tombe en passant par les positions 2 et 3. Finalement, il remonte pour atteindre les positions 4 et 5.
Si on considère que le pendule ne subit aucune perte d’énergie, le mouvement de va-et-vient continue sans cesse puisque l’énergie totale du pendule est conservée.
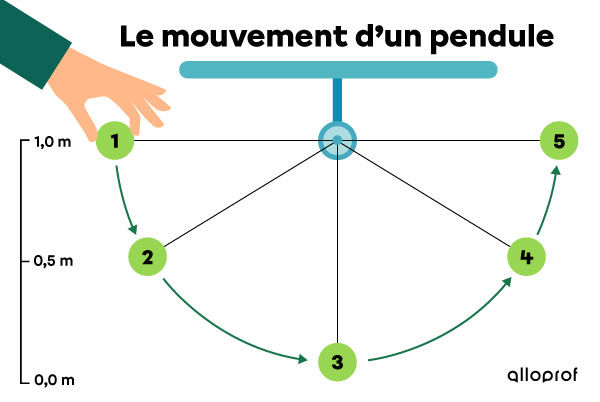
Le mouvement d’un pendule
|
La variation de l’énergie potentielle gravitationnelle et cinétique d’un pendule en fonction de sa position |
||||
|
Position |
Hauteur |(\text{m})| |
Énergie potentielle gravitationnelle |(\text{J})| |
Vitesse |(\text{m/s})| |
Énergie cinétique |(\text{J})| |
|---|---|---|---|---|
| 1 | |1{,}0| | |9{,}8| | |0{,}0| | |0{,}0| |
| 2 | |0{,}5| | |4{,}9| | |3{,}13| | |4{,}9| |
| 3 | |0{,}0| | |0{,}0| | |4{,}43| | |9{,}8| |
| 4 | |0{,}5| | |4{,}9| | |3{,}13| | |4{,}9| |
| 5 | |1{,}0| | |9{,}8| | |0{,}0| | |0{,}0| |
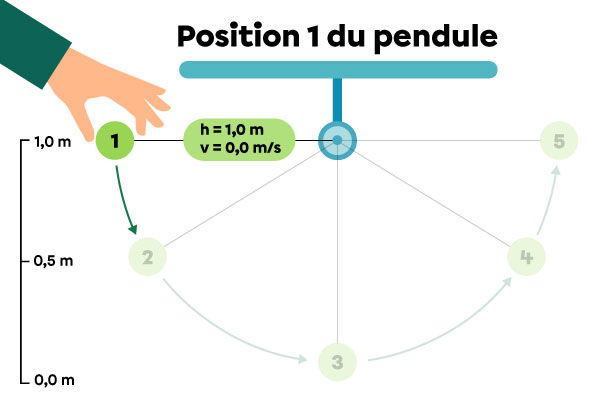
Position 1 : le pendule est immobile à sa hauteur maximale.
|\begin{align} E_{pg}&=mgh\\
E_{pg}&=1{,}0\ \cancel{\text{kg}}\times 9{,}8\ \text{N/}\cancel{\text{kg}} \times 1{,}0\ \text{m}\\
E_{pg}&=9{,}8\ \text{J}\end{align}|
|\begin{align} E_k&=\dfrac{1}{2}mv^2\\
E_k&=\dfrac{1}{2} \times 1{,}0 \text{kg}\times (0{,}0\ \text{m/s})^2\\
E_k&=0{,}0\ \text{J}\end{align}|
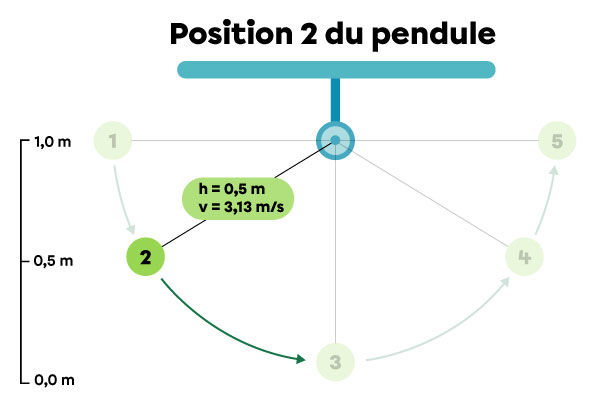
Position 2 : le pendule perd de l’énergie potentielle gravitationnelle, mais acquiert de l’énergie cinétique.
|\begin{align} E_{pg}&=mgh\\
E_{pg}&=1{,}0\ \cancel{\text{kg}}\times 9{,}8\ \text{N/}\cancel{\text{kg}} \times 0{,}5\ \text{m}\\
E_{pg}&=4{,}9\ \text{J}\end{align}|
|\begin{align} E_k&=\dfrac{1}{2}mv^2\\
E_k&=\dfrac{1}{2} \times 1{,}0 \text{kg}\times (3{,}13\ \text{m/s})^2\\
E_k&=4{,}9\ \text{J}\end{align}|
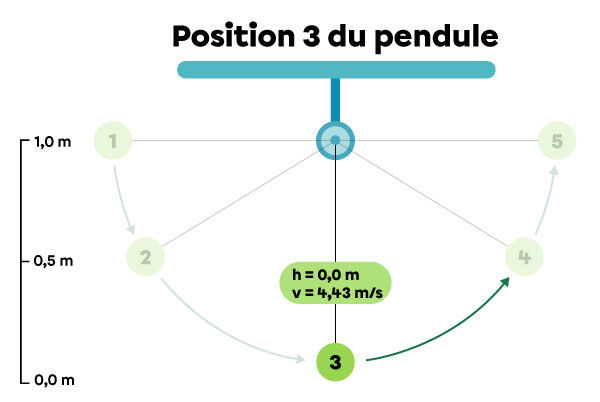
Position 3 : le pendule frôle le sol et atteint sa vitesse maximale.
|\begin{align} E_{pg}&=mgh\\
E_{pg}&=1{,}0\ \cancel{\text{kg}}\times 9{,}8\ \text{N/}\cancel{\text{kg}} \times 0{,}0\ \text{m}\\
E_{pg}&=0{,}0\ \text{J}\end{align}|
|\begin{align} E_k&=\dfrac{1}{2}mv^2\\
E_k&=\dfrac{1}{2} \times 1{,}0 \text{kg}\times (4{,}43\ \text{m/s})^2\\
E_k&=9{,}8\ \text{J}\end{align}|
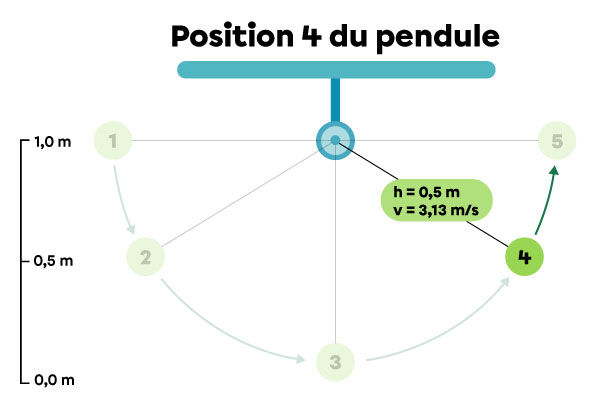
Position 4 : le pendule gagne de l’énergie potentielle gravitationnelle, mais perd de l’énergie cinétique.
|\begin{align} E_{pg}&=mgh\\
E_{pg}&=1{,}0\ \cancel{\text{kg}}\times 9{,}8\ \text{N/}\cancel{\text{kg}} \times 0{,}5\ \text{m}\\
E_{pg}&=4{,}9\ \text{J}\end{align}|
|\begin{align} E_k&=\dfrac{1}{2}mv^2\\
E_k&=\dfrac{1}{2} \times 1{,}0 \text{kg}\times (3{,}13\ \text{m/s})^2\\
E_k&=4{,}9\ \text{J}\end{align}|
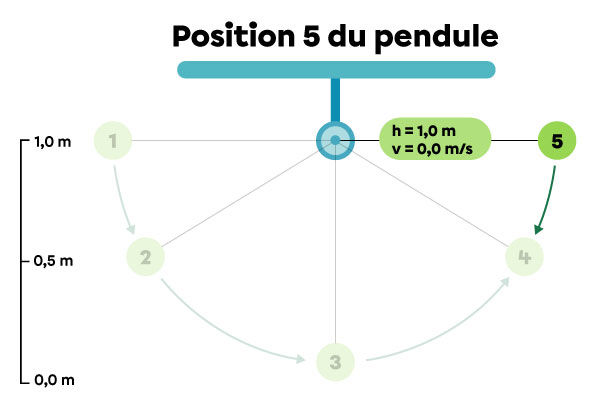
Position 5 : le pendule est immobile à sa hauteur maximale juste avant de retomber.
|\begin{align} E_{pg}&=mgh\\
E_{pg}&=1{,}0\ \cancel{\text{kg}}\times 9{,}8\ \text{N/}\cancel{\text{kg}} \times 1{,}0\ \text{m}\\
E_{pg}&=9{,}8\ \text{J}\end{align}|
|\begin{align} E_k&=\dfrac{1}{2}mv^2\\
E_k&=\dfrac{1}{2} \times 1{,}0 \text{kg}\times (0{,}0\ \text{m/s})^2\\
E_k&=0{,}0\ \text{J}\end{align}|
Finalement, le pendule retombera vers les positions 4, 3, 2 et 1 dans un mouvement de va-et-vient.
À voir aussi
Exercice
Référence
Stanton, C. (2021, 22 janvier). Mission Red Bull Stratos : histoire d'un record. RedBull. https://www.redbull.com/ca-fr/red-bull-stratos-baumgartner-saut-record