Best Of

Re salut!

C'est excellent, tu as bien compris, bon travail! 😁

Si tu as d'autres questions, on est là! :)

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Salut!

Paulette veut partager 5⅓ tasses de jus en 8 personnes. Il faut donc diviser 5⅓ par 8 pour trouver la quantité que chacune des 8 personnes aura dans son verre.

Ensuite, tu dois vérifier si cette quantité est supérieure ou inférieure à 3/4, car les verres à Paulette ne peuvent contenir que 3/4 de tasse de liquide. Si elle est supérieure à 3/4, cela signifie que les verres ne sont pas assez grands, donc le verre débordera à cause du surplus de jus. Si elle est inférieure à 3/4, cela signifie que les verres sont assez grands et qu'il y a de la place pour ajouter du liquide.

Je te laisse essayer avec ces indices. Voici des fiches qui pourraient t'être utiles :

• La division de fractions | Secondaire | Alloprof
• La soustraction de fractions | Secondaire | Alloprof

Si tu as d'autres questions, n'hésite pas à nous réécrire! :)

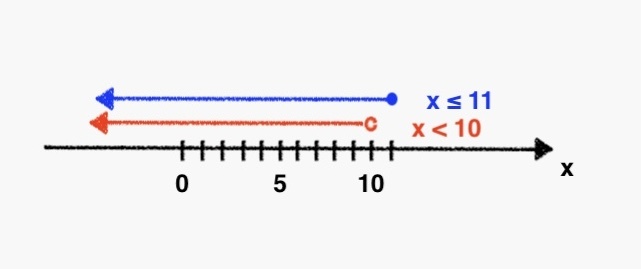
• La restriction sur la non négativité de la racine carrée d'un nombre ou une expression => 11 - x ≥ 0 donc que x ≤ 11
• Par ailleurs l'inégalité elle-même te dit que √(11 - x) > 1
• Au carré l'inégalité devient 11 - x > 1² => 11 - x > 1
• Ce qui revient à x < 10
• Tu as donc deux restrictions x ≤ 11 et x < 10, l'intersection des deux restrictions est x < 10 c'est-à-dire x appartient à -∞,10[

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Salut!

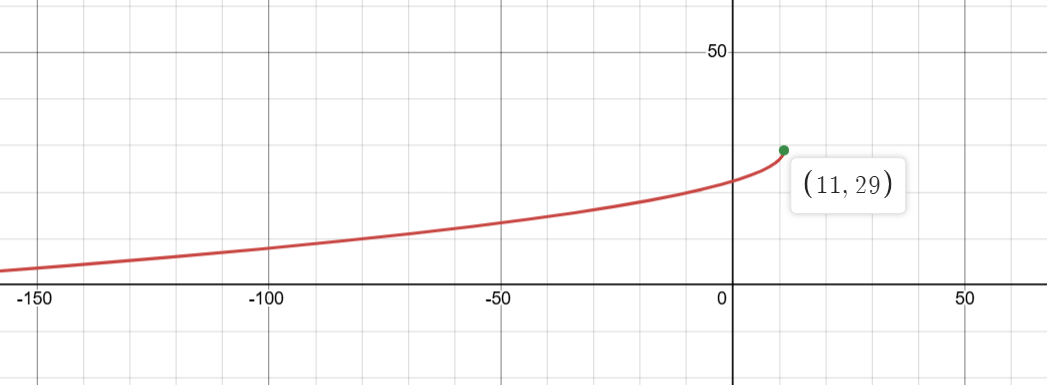
Tout d'abord, traçons le graphique de la fonction \(f(x)=-2\sqrt{11-x}+29\) :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Le sommet (h, k) est (11, 29). Regardons pourquoi nous avons eu ce graphique.

On peut réécrire la fonction comme ceci pour avoir la forme canonique :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

$$f(x)=-2\sqrt{11-x}+29$$

$$f(x)=-2\sqrt{-x+11}+29$$

$$f(x)=-2\sqrt{-(x-11)}+29$$

Il faut absolument avoir la forme canonique pour pouvoir identifier nos paramètres a, b, h et k correctement! En effet, cela nous a permis de déterminer que le paramètre h est de 11, et non -11.

De plus, puisque le paramètre b est négatif, la branche du graphique de la fonction racine carrée est orientée vers la gauche. Donc, h est la plus grande valeur possible de x, et non la plus petite!

Voici une fiche qui pourrait t'être utile pour mieux comprendre l'effet de chaque paramètre : Le rôle des paramètres dans une fonction racine carrée | Secondaire | Alloprof

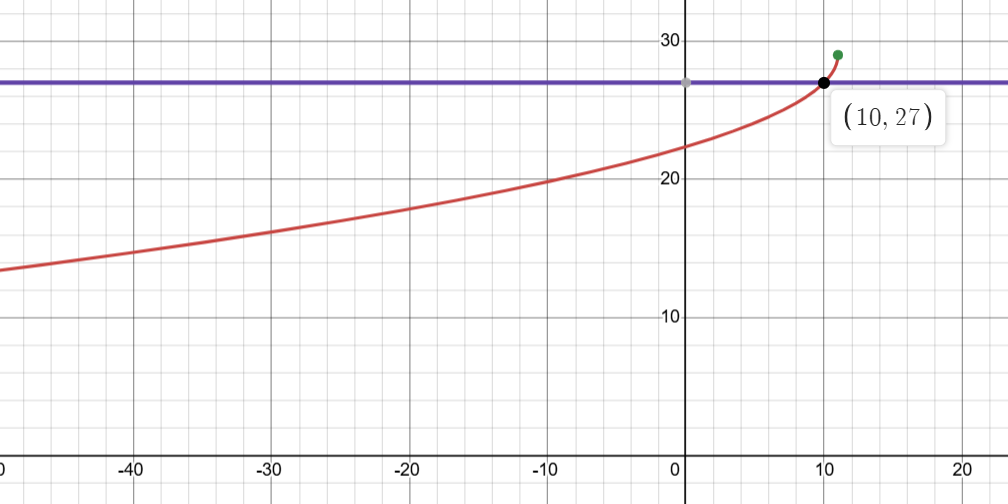
Ensuite, on cherche l'intervalle pour laquelle la fonction est inférieure à y=27 (droite horizontale mauve) :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Avec e graphique, on constate que la fonction est inférieure à 27 sur l'intervalle ]-∞, 10[, ce qui concorde avec les calculs du corrigé.

Dans tes calculs, tu as la bonne démarche, mais à la fin, tu as un nombre qui ne figure nulle part dans tes calculs (le -11), ce qui t'indique déjà que ce n'est pas la bonne réponse :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Tu dois vraiment te fier aux résultats obtenus avec tes calculs pour trouver la réponse finale. On sait que x doit être plus petit ou égal à 11 en posant la restriction (car la fonction cesse d'exister à partir de x=11, c'est-à-dire le sommet à x=h), et la solution nous dit qu'on est inférieur à y=27 si x<10. Ainsi, puisque la solution respecte la restriction, la réponse finale sera x<10, ou ]-∞, 10[.

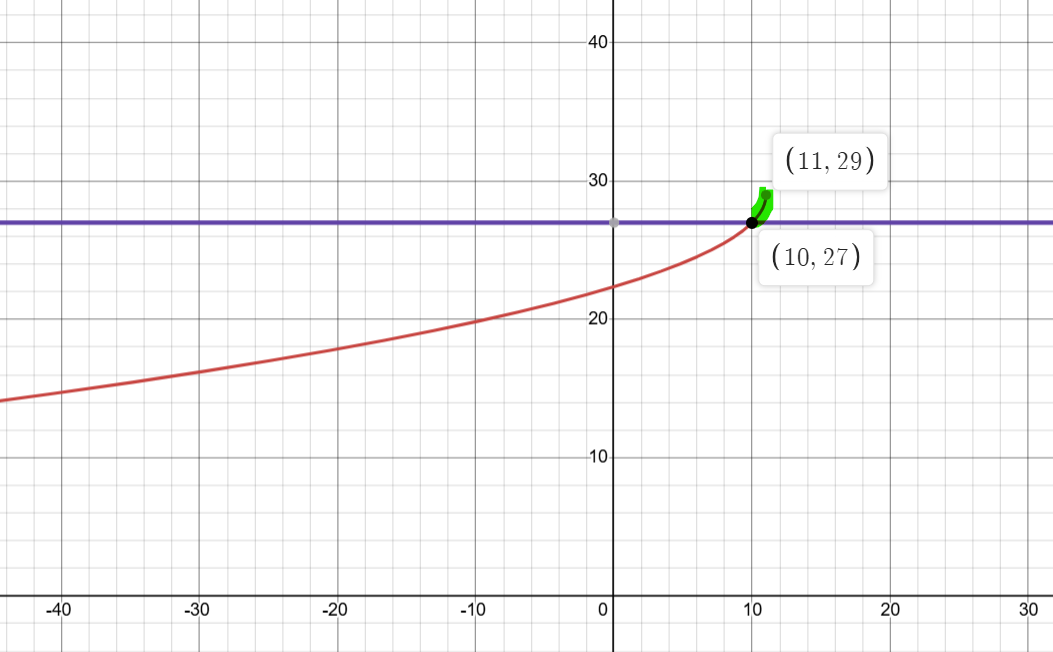
Si on cherchait l'intervalle pour lequel la fonction est supérieure à y=27, donc on cherche l'intervalle de cette partie :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

On peut constater à l'aide du graphique que la réponse serait ]10, 11].

À l'aide de calculs, on aurait la restriction x≤11, et la même solution, mais avec le signe inverse : x>10. Puisque la solution trouvée est affectée par la restriction, l'intervalle final serait donc x>10 et x≤11, donc ]10, 11], ce qui concorde avec ce qu'on peut observer à l'aide du graphique.

J'espère que c'est plus clair pour toi! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)

Salut!

Tu peux calculer la contribution de chacun en calculant le rapport : montant que la personne a apporté / montant total apporté

Le montant total est de 27 000$ + 54 000$ + 81 000$ = 162 000$.

Ainsi, la première personne a contribué en apportant : 27 000 / 162 000 = 16,67% du montant total. Elle doit donc recevoir 16,67% du montant à partager.

Je te laisse faire les autres calculs. J'espère que c'est plus clair pour toi! :)

Salut !

Alloprof ne corrige pas les exercices, mais permet plutôt une meilleure compréhension de la matière et de la démarche à suivre.

Y a-t-il un exercice en particulier pour lequel tu as de la misère ou des doutes ?

Si tu as d'autres questions, n'hésite pas !

Bonne journée !