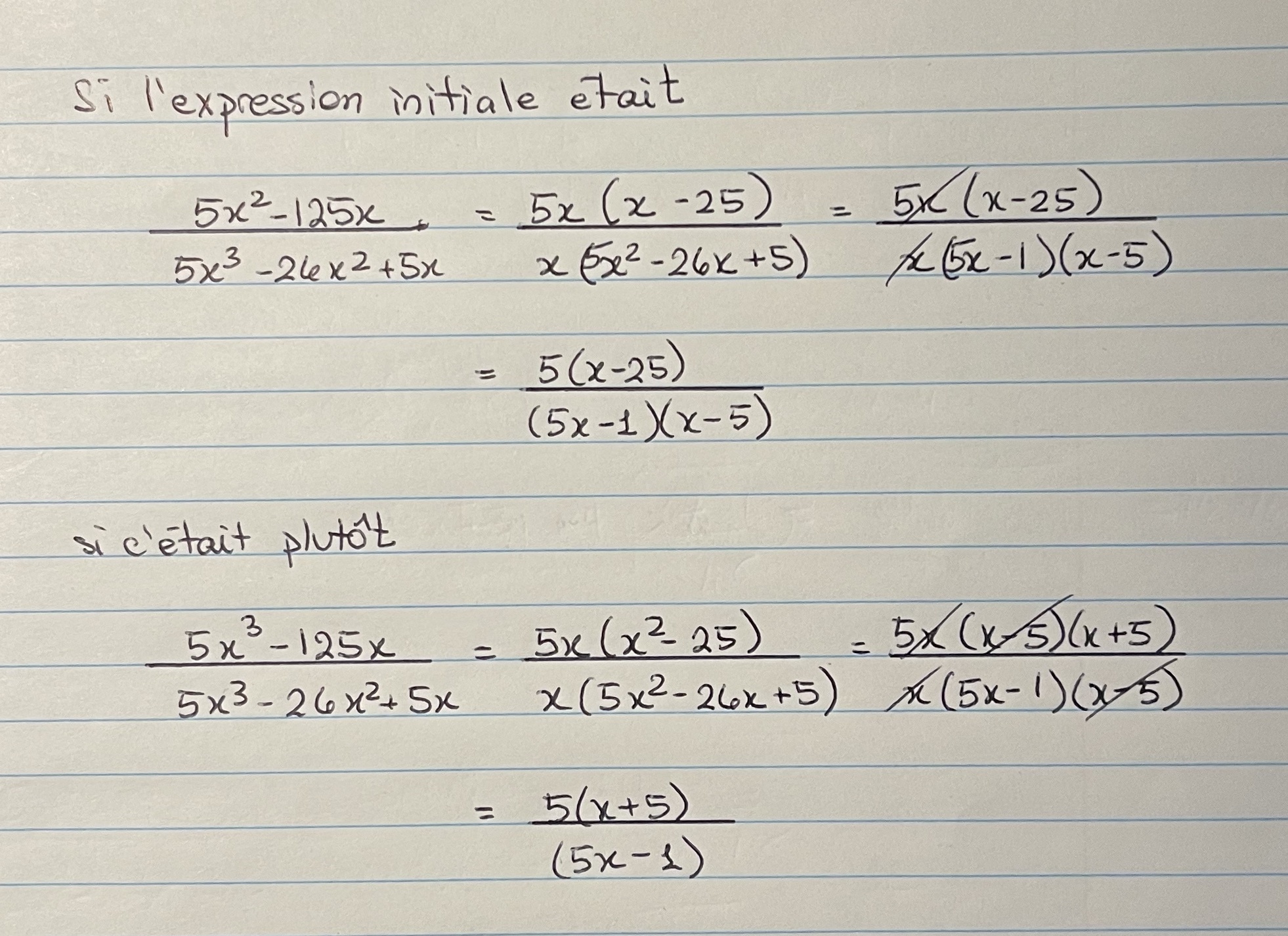Best Of
Re: Question
Merci pour ta question!
D'abord, rappelons nous de la définition des concentrations en parties par million :
$$ ppm = \frac{m_{soluté}}{m_{solution}}•1000000 $$
Légende :
• ppm : parties par million
• m soluté : masse du soluté
• m solution : masse de la solution
Rappelons nous aussi de la définition des concentrations en g/L :
$$ C = \frac{m}{V} $$
Légende :
• C : concentration (g/L)
• m : masse (g)
• V : volume (L)
À première vue, les deux mesures semblent très différentes. Cependant, si tu connais la densité du solvent, tu peux trouver sa masse. Dans le cas de l'eau, sa densité est de 1000 g/L. Ainsi, on peut rapporter la concentration en g/L à une concentration en g de soluté par g de solvent :
$$ \frac{0,773\:g}{L}=\frac{0,773\:g}{1000\:g} = 0,773 $$
Puis, on peut simplement multiplier ce rapport par 1000000 pour trouver sa valeur en ppm :
$$ 0,773 • 1000000 = 773 000 \: ppm $$
Voilà!
Cette fiche du site d'Alloprof explique les calculs de concentration en ppm :
N'hésite pas si tu as d'autres questions!
Re: Question
Bonjour DragonRouge669,
Merci pour ta question :)
Je t'envoie ici un lien vers une fiche qui contient activités et exemples sur le volume. Tu y trouveras aussi une mini récup au besoin: https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/l-aire-et-le-volume-des-solides-m1243
Voici une fiche par rapport aux unités de mesure du volume et à leur conversion: https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/les-unites-de-volume-et-leur-conversion-m1392
N'hésite pas si tu as d'autres questions et bonne chance pour ton examen :)
Sandrine
Re: Question
Bonjour!
Attribut du sujet est la fonction occupée par l'adjectif « vieilles ». L'attribut du sujet est à l'étude à partir de la 5e année, il est donc possible de réviser cette fonction syntaxique en 6e année! :D
Cette fiche sur l'attribut du sujet pourrait t'aider à comprendre :
En ce qui concerne l'accord, je te suggère de relire la réponse à ton autre question! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Merci pour ta question!
La question de l'IA générative, comme ChatGPT, est très complexe.
D'un côté, il s'agit d'une avancée massive d'un point de vue technologique. Des tâches routinières, répétitives et parfois inutiles peuvent être éliminées ou fortement raccourcies au clic d'un bouton. Bref, un nouvel assistant virtuel presque aussi intelligent que nous est maintenant accessible.
D'un autre perspective, cette technologie a le potentiel de tout changer. Elle pourrait éliminer ou fortement réduire certains emplois, dont les tâches sont maintenant plus facilement exécutables par IA. Elle pourrait accélérer le déclin de certains apprentissages, si certains élèves ne font que s'y référer sans apprendre la matière par eux-mêmes. Elle pourrait même avoir d'autres effets néfastes sur le monde, comme la création de contenus de désinformation.
Si je parle en tant que personne qui travaille chez Alloprof, mais non au nom de la compagnie elle-même, je ne suis pas trop inquiet par rapport à mon emploi. Au contraire, il y a beaucoup de potentiel pour utiliser l'IA chez soi ou au travail et l'IA ne remplacera pas le travail de modérateur. En effet, certaines questions sont trop complexes, d'autres sont émotionnellement difficiles, et certaines nécessitent des connaissances que les IA n'ont simplement pas. L'humanité des modérateurs est essentielle au fonctionnement du site, même si les modérateurs humains sont un peu plus lents!
Bref, voilà mon opinion nuancée sur l'IA. J'espère que cela aide ta réflexion.
N'hésite pas si tu as d'autres questions!
Re: Question
Bonjour!
Ici, «vieilles » est un adjectif qui qualifie les sacoches. Même si les mots ne sont pas collés, on doit toujours accorder l'adjectif avec son donneur d'accord. Ici, le donneur d'accord de « vieilles » est sacoches, c'est pourquoi on accorde au féminin pluriel! :D
Voici une fiche sur les adjectifs qui pourrait t'aider :
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Salut!
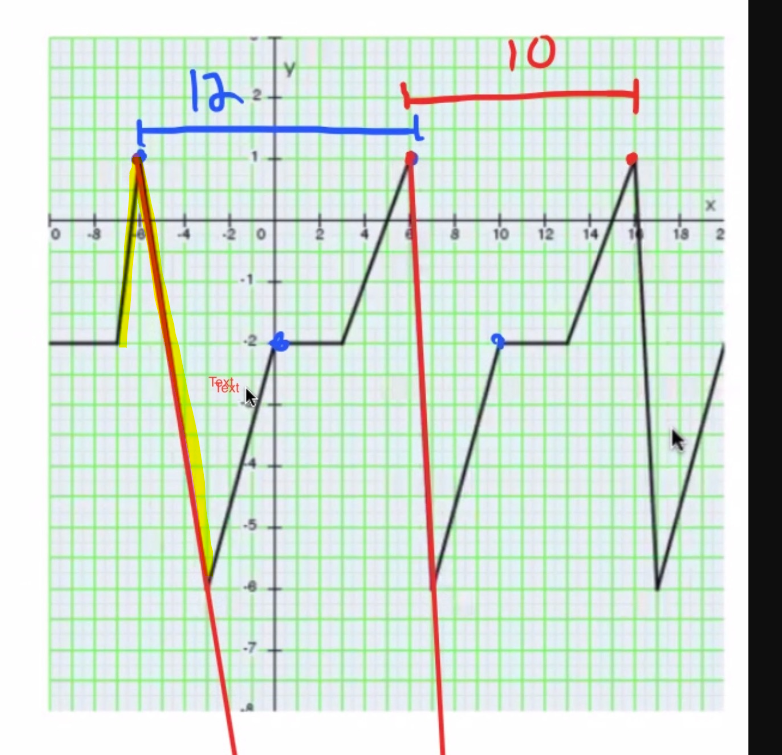
On dirait en effet qu'il y a une erreur dans le dessin de cette partie de la fonction :
Je dirais donc que la période est de 10, et qu'il ne faut pas tenir compte de la fonction entre x=-7 à x=-3.
Je te conseille d'en faire part à ton professeur pour qu'il puisse ajuster l'exercice.
Si tu as d'autres questions, n'hésite pas! :)
Re: Question
Bonjour !
Si tu veux tout savoir, la voie lactée est énorme et tu ne pourras jamais nombrer tout ce qui s'y trouve, mais par exemple, il y a certains astres, des planètes, le soleil, des étoiles, des lunes, etc. Si tu veux plus de précisions, je t'invite à suivre ce lien, qui mène à la voie lacté sur Wikipédia, qui te donnera plus d'informations que moi ;)
Bonne journée,
-Plume
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
Donc, petit rappel: arrondir un nombre consiste à donner une valeur rapprochée du nombre connu. De plus, si le chiffre à droite de la position à arrondir est supérieur ou égal à 5 (soit 5, 6, 7, 8 ou 9), on ajoute 1 au chiffre de la position à arrondir. Mais si le chiffre suivant est inférieur à 5 (soit 0, 1, 2, 3 ou 4), alors il faut conserver ce chiffre.
Donc, arrondir au dixième correspond à arrondir à 1 chiffre après la virgule.
Par exemple:
Nous souhaitons arrondir 6,379 au dixième. L’arrondi est 6,4. puisque le deuxième chiffre, donc celui à droite des dixièmes, après la virgule, le 7, est supérieur à 5.
Si on te demande d'arrondir au centième, on te demande d'arrondir à 2 chiffres après la virgule.
Par exemple:
L’arrondi de 14,75638 est 14,76. car le troisième chiffre après la virgule, le chiffre à droite des centièmes, 6 est supérieur à 5.
Pour t'aider, tu dois bien connaitre le nom des positions décimales (centième, dixième, etc.)
Si tu veux plus d'exemples, tu peux consulter la fiche suivante:
N'hésite pas à revenir nous voir si tu as d'autres questions.
Bonne journée,
Karen
Re: Question
Salut !
Pour que ce soit plus aisé pour toi, tu peux écrire les exposant à l'aide du chapeau. 5x2 devient 5x^2. Si je réécris ton équation, cela donne ceci :
$$ \frac{5x^2-125x}{5x^3-26x^2+5x}=\frac{5x(x^2-25)}{(x-5)(5x^2-2)} $$
Il semble y avoir une erreur quelque part au numérateur, car tu passe de \(5x^2-125x\) à \(5x(x^2-25)\). Un \(x\) s'est ajouté. La première étape est en effet d'effectuer des mise en évidence simple. Ainsi, tu peux mettre en évidence \(x\) au dénominateur plutôt pour donner l'expression suivante.
$$ 5x^3-26x^2+5x=x(5x^2-26x+5) $$
L'expression \(5x^2-26x+5\) est plus facile à factoriser.
$$ 5x^2-26x+5=(x-5)(5x+1) $$
Tu peux ainsi voir qu'il serait possible de retrouver une des expressions du dénominateur au numérateur.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !