Best Of

Bonjour SoleilLogique441,

Merci pour ta question :)

Tes démarches pour l'autobus et le spectacle sont parfaites :) Pour le chocolat, de ce que j'ai compris, le prix coûtant d'une barre est celui de la position des centaines dans la masse, c'est-à-dire 3$. Si on vend les tablettes 5$ et qu'elles coûtent 3$, on fait un profit de 2$.

Ensuite, tu as raison, on multiplie par le nombre de barres par boîte, donc 2x12=24. Puis on multiplie par le nombre de boîtes: 24x16=384$.

Continue comme ça, tu es bien parti! N'hésite pas si tu as d'autres questions :)

Sandrine

Bonjour PamplemousseTurquoise7902,

Merci pour ta question :)

Le principe du tableau de signe, c'est de factoriser ton polynôme, dans cet exemple, on factorise 3x^2-17x-6x en 3(x+1/3)(x-6). On peut voir facilement dans cette factorisation que si x=-1/3 ou x=6, une des deux parenthèse sera égale à 0 et donc que l'expression au complet sera égale à zéro.

Ces endroits où le polynôme est égale 0 sont des points repères. Il s'agit de x=-1/3 et x=6 dans ce cas. Ça signifie qu'entre ces points, la fonction va se comporter de la même façon. La première ligne du tableau sert à mettre les points repères en évidence. Ensuite, les lignes du tableau servent à identifier le signe de certaines parties de la fonction. Par exemple, la parenthèse (x+1/3) est-elle positive ou négative avant x=-1/3? Puis entre x=-1/3 et 6? Puis après6? Le même raisonnement s'effectue pour la parenthèse (x-6).

La dernière ligne sert à déterminer le signe de toute la fonction au complet: comme il s'agit d'une multiplication des parenthèses (x+1/3) et (x-6), si une des deux est négative, la multiplication sera négative. Si elles sont les deux de même signe, la multiplication sera positive. Tu sais ainsi ta fonction est positive ou négative dans quel intervalle.

Je suis d'accord avec toi, ça peut être mélangeant et il y a peut-être d'autres méthodes. Cependant, l'avantage de cette méthode, c'est qu'elle est systématique et donc diminue beaucoup les chances de se tromper une fois qu'on la comprend.

N'hésite pas si tu as besoin d'aide à nouveau :)

Sandrine

Salut!

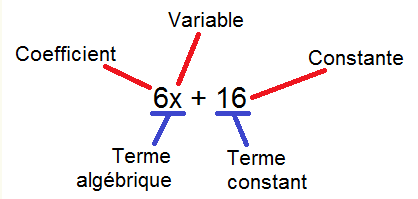
Une expression algébrique est un ensemble de termes algébriques (des termes avec des lettres) et constants (des termes numériques, sans lettre) reliés entre eux par des additions ou des soustractions.

Par exemple, ceci est une expression algébrique composée de deux termes :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Construire une expression algébrique, c'est simplement créer une chaîne d'addition ou de soustraction de termes.

Par exemple, si je dis que je mange un certain nombre de pommes aujourd'hui, et que je compte en manger le double demain, je peux construire cette expression algébrique pour déterminer le nombre de pommes mangées après ces deux jours : x + 2x, où x est le nombre de pommes que j'ai mangées aujourd'hui.

Je t'invite à consulter la fiche suivante :

• Algèbre - Expressions algébriques | Alloprof

Et à revenir nous voir si tu as d'autres questions! :)

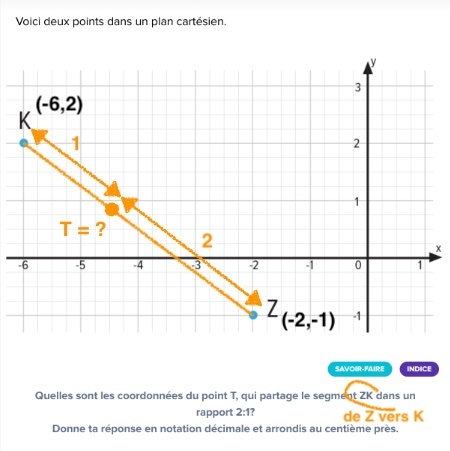
Selon le graphique

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

• on identifie le point de départ Z = (-2,-1)
• et le point d'arrivée K = (-6,2)

le point de partage est déterminé selon

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

où k = partie/tout = 2/3

donc en x tu as

-2 + (2/3)(-6+2) = -2 + (2/3)(-4) = -2 - 8/3 = -14/3

et en y tu as

-1 + (2/3)(2+1) = -1 + 2 = +1

=> T = (-14/3, 1) = (-4.67, 1)

Est-ce une bonne réponse? À l'oeil on dirait bien que oui

Je n'ai pas été capable de voir directement les images que tu mentionnes, mais je peux t'aider à clarifier ton problème avec la méthode que tu décris.

Voici un résumé de ce que tu sembles vouloir faire :

1. Rendre les équations égales à zéro : Lorsque tu veux trouver les zéros d'une fonction quadratique f(x)f(x)f(x), tu dois d'abord la transformer en une équation de la forme générale ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0.
2. Utiliser la formule quadratique : La formule quadratique que tu as mentionnée est la bonne pour résoudre une équation de la forme ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0. Cette formule est :
3. x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}x=2a−b±b2−4ac​​
   • aaa, bbb et ccc sont les coefficients de l'équation quadratique.
   • Le terme sous la racine, Δ=b2−4ac\Delta = b^2 - 4acΔ=b2−4ac, est appelé le discriminant et il détermine le nombre de solutions :
     • Si Δ>0\Delta > 0Δ>0, il y a deux solutions réelles distinctes.
     • Si Δ=0\Delta = 0Δ=0, il y a une solution réelle (racine double).
     • Si Δ<0\Delta < 0Δ<0, il n'y a pas de solution réelle (les solutions sont complexes).
4. Pourquoi ça n’a pas fonctionné ?
   • Forme incorrecte : Si tu n’as pas mis la fonction sous la bonne forme ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0, la formule quadratique ne fonctionnera pas. Vérifie que tu as bien isolé tous les termes et que l’équation est sous cette forme avant d’appliquer la formule.
   • Erreur dans le calcul : Parfois, une petite erreur dans les calculs du discriminant ou dans l’application de la formule peut faire échouer le processus. Vérifie chaque étape.
5. Transformation en forme générale : Si dans le corrigé, on te demande de transformer la fonction en "forme générale", cela signifie généralement qu'il faut la réécrire sous la forme standard d’une équation quadratique :
6. f(x)=ax2+bx+cf(x) = ax^2 + bx + cf(x)=ax2+bx+c
7. C’est cette forme que tu utilises pour appliquer la formule quadratique.

Étapes à suivre :

1. Vérifie ta fonction : Assure-toi qu’elle est bien de la forme ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0.
2. Calcule le discriminant Δ=b2−4ac\Delta = b^2 - 4acΔ=b2−4ac : Ce discriminant te dira si la fonction a des zéros réels ou non.
3. Applique la formule : x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}x=2a−b±b2−4ac​​
4. Interprète le résultat :
   • Si tu trouves Δ>0\Delta > 0Δ>0, tu devrais obtenir deux solutions pour xxx.
   • Si Δ=0\Delta = 0Δ=0, il y a une seule solution (racine double).
   • Si Δ<0\Delta < 0Δ<0, il n’y a pas de solution réelle.