Best Of

bonjour,

la différence entre les nombre premiers et les nombres composer

c'est que les nombres premier on seulement 2 diviseur, 1 et lui même

les nombres composer ont plus que 2 diviseurs

et en passent les nombres carrée sont des nombres qui on les même facteur comme 6x6=36, donc 36 est un nombre carré

voilà !!!

Bonjour j'aurais une question quelle est la différance entre un nombre premier et composer

Merci

Tu as f(x) = 3x + 5

et g(f(x)) = x + 1

on dit que g est une fonction polynomiale de degré 1 donc

g(z) = az + b (1)

J'ai pris z pour éviter toute confusion.

Comme Ramzi l'avait explIqué initialement, tu as donc

g(f(x)) = g(3x + 5) = a(3x + 5) + b = (3a)x + (5a +b)

et

g(f(x) = x + 1

les termes correspondants sont égaux

=> 3a = 1 et a = 1/3

=> 5a + b = 1 ; 5(1/3) + b = 1 et b = -2/3

On a donc trouvé le a et le b de la fonctIon g qu'on avait exprimée en (1)

g(z) = z/3 - 2/3

Allo FraiseAdorable5247,

Merci pour ta question!

C'est normal que tu retournes à g(x), car tu fais l'opération inverse. Je ne crois pas que tu as besoin d'isoler ton x. tu dois seulement le remplacer par l'autre fonction.

Je te suggère d'aller voir les exemples de la fiche suivante:

J'espère t'avoir aidé!

Lea-Kim

Bonsoir, FraiseAdorable5247!

Tu en auras peut-être en devoir, mais sinon tu peux demander à ton enseignant s'il en a! Une recherche en ligne pourrait être fructueuse, ou même acheter des cahiers de mathématiques convenables à ton niveau.

Si on t'a déjà donné des exercices, concentre-toi sur ceux-ci. Il est bien de résoudre une autre fois d'anciens problèmes pour s'assurer de la compréhension.

Je t'invite à consulter la section à cet effet.

N'hésite pas à poser d'autres questions!

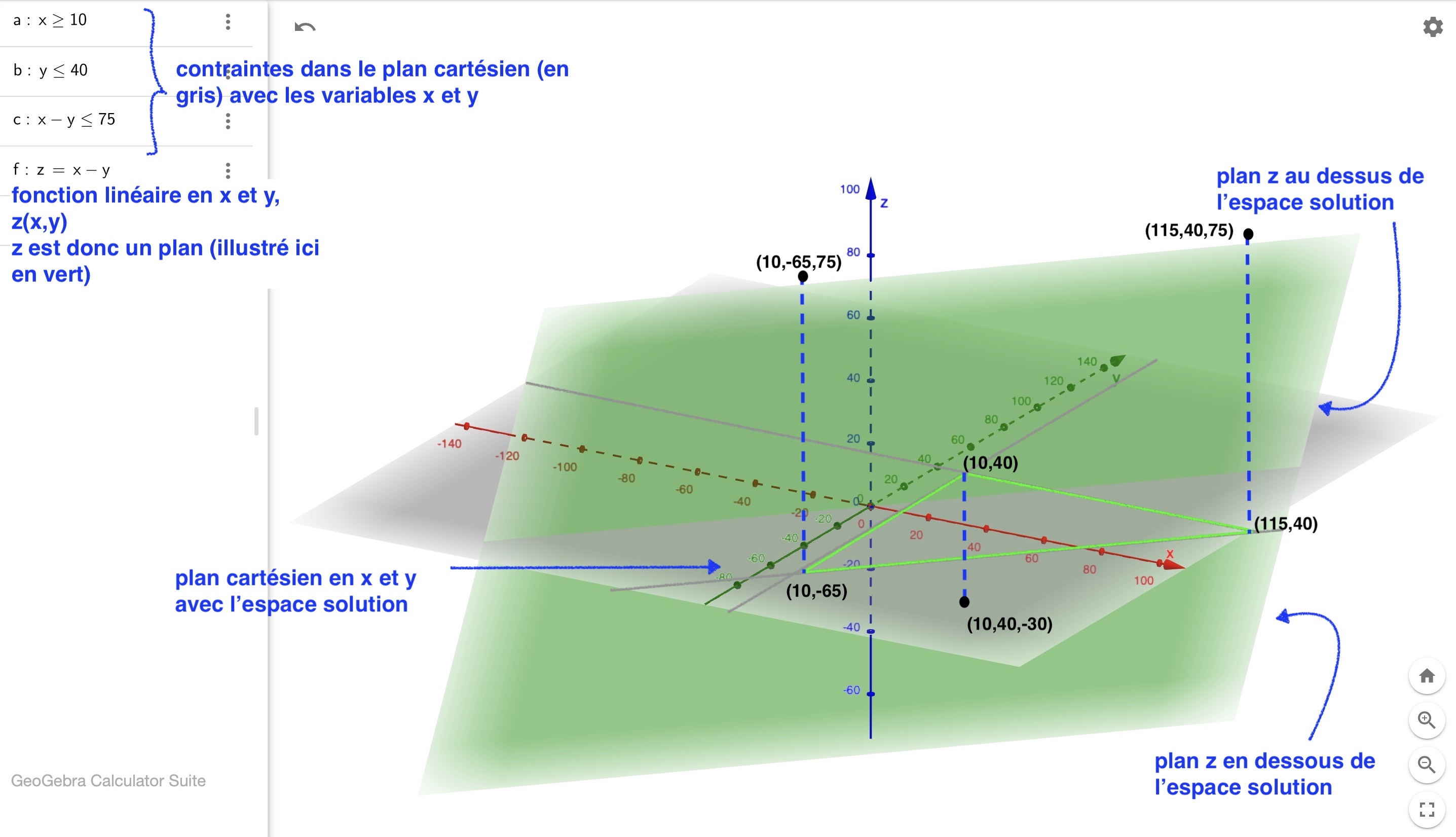
Comme Katia l'a indiqué, c'est essentiellement parce que tout est linéaire on a des droites comme contraintes générant un espace solution dans le plan cartésien xy et une fonction à maximiser ou minimiser dans un plan xyz.

Il faut imaginer ceci en trois dimensions: un gros panneau croisant le plan xy (c'est à dire dans le plan xyz avec z=0)

J'ai essayé d'illustrer cela avec plus ou moins de succès.

L'espace solution est délimité par les sommets (10,-65), (10,40) et (115,40)

Note qu'ici la solution qui maximise la fonction est non seulement aux sommets (10,-65) et (115,40) mais tout le long du segment x-y =75 d'un sommet à l'autre.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Bonsoir, CobraRomantique386!

D'abord, tu dois trouver les zéros de la fonction.

$$ x_{1,2} = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

Si un trinôme de la forme $$ {a}x^2+bx+c $$ est factorisable, alors on peut l'écrire sous la forme

$$ {a}(x-x_1)(x-x_2) $$

où x1 et x2 sont les deux racines calculées avec la formule quadratique.

N'hésite pas si tu as d'autres questions!