Best Of

Bonjour,

Pour savoir si deux droites sont parallèles distinctes, il suffit de comparer leurs pentes. Deux droites sont parallèles si elles ont la même pente et elles sont dites distinctes si elles n'ont pas la même ordonnée à l'origine, c'est-à-dire si elles ne sont pas superposées.

Par exemple, si les équations des droites sont sous la forme y=mx+b, elles sont parallèles si les valeurs de m (la pente) sont identiques. Cependant, elles sont parallèles distinctes si, en plus, les valeurs de b (l'ordonnée à l'origine) sont différentes, car cela signifie qu'elles ne se chevauchent pas.

ex:

y1 = 2x + 3 et y2 = 2x+10 sont parallèles distinctes.

y1 = 2x + 3 et y2 = 2x+3 sont parallèles confondu

y1 = 3x + 3 et y2 = 2x+3 ne sont pas parallèles

N'hésite pas si tu as d'autres question cela nous fera plaisir :)

Bonne journée

Je ne comprent pas La partie'' Vérifier si un point appartient à la droite''

Salut!

Tu dois utiliser l'équation de la droite pour vérifier si un certain point de coordonnées x et y appartient bien à cette droite.

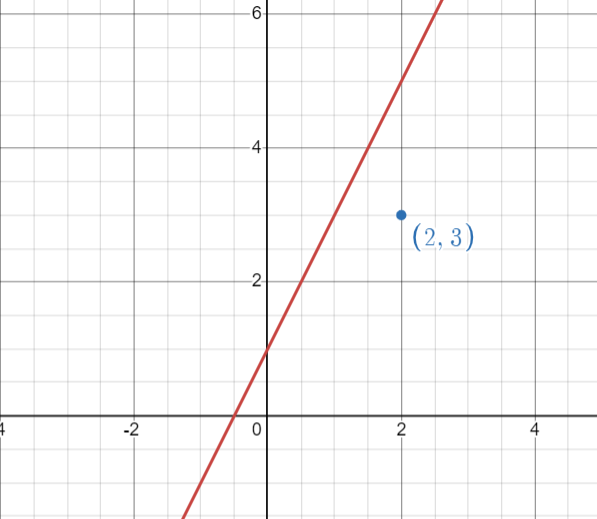
Prenons un exemple. Nous avons le point (2, 3) et la droite y=2x+1. Pour vérifier si ce point appartient à cette droite, tu dois insérer les coordonnées dans l'équation, et vérifier si l'égalité est respectée :

$$3=2(2)+1$$

$$3=4+1$$

$$3=5$$

L'égalité est fausse, ce qui signifie que ce point n'appartient à la droite y=2x+1.

On peut le constater en analysant le graphique :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

J'espère que c'est plus clair pour toi! :)

Salut MaringouinAdorable8064!

Merci pour ta question. :)

Il est toujours possible de poser tes questions sur la Zone, si telle est ta question!

Dès qu'un membre de la modération sera présent, il prendra soin de répondre à ta ou tes questions!

En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!

À bientôt,

Océane :)

Salut,

Comme les coordonnées du point mileu du segment AB sont à mi-chemin entre le point A et le point B, il te suffit de calculer la distance en x et y entre le point A et le milieu:

Distance en x = (7 - 1) = 6

Distance en y = -3 - 3 = -6

Puis, pour parcourir la deuxième moitié du chemin, on les multiplie par 2 et on les additionne aux coordonnées du point A, ce qui nous donnera les coordonnées du point B.

N'hésites pas si tu as d'autres questions

Salut !

Pour compléter la réponse de , tu peux en effet utiliser la logique qui veut que le point milieu se trouver exactement entre les deux points et la distance entre ce pont et le point A est exactement la moitié de la distance entre A et B.

$$ \text{Point milieu} = \left( \dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2} \right) $$

J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !

Bonne journée !