Matières
Niveaux
Le point de partage et le point milieu d'un segment
Fiche | Mathématiques
Secondaire
4-5
-
Un point de partage d'un segment est un point qui sépare ce segment en 2 selon un rapport donné. Le rapport est entre 0 et 1 inclusivement.
-
Le point milieu est le point de partage qui sépare le segment initial en 2 segments égaux.
Le point de partage et le point milieu d'un segment - Explication
Le point de partage d'un segment
Les coordonnées du point de partage |P| du segment |\overline{AB}| sont données par la formule suivante.
||(x_{\small{P}},y_{\small{P}})=\big(x_1+k(x_2-x_1),y_1+k(y_2-y_1)\big)||où
|A(x_1,y_1):| la 1re extrémité (point de départ)
|B(x_2,y_2):| la 2e extrémité
|P(x_{\small{P}},y_{\small{P}}):| le point de partage
|k:| le rapport partie-tout
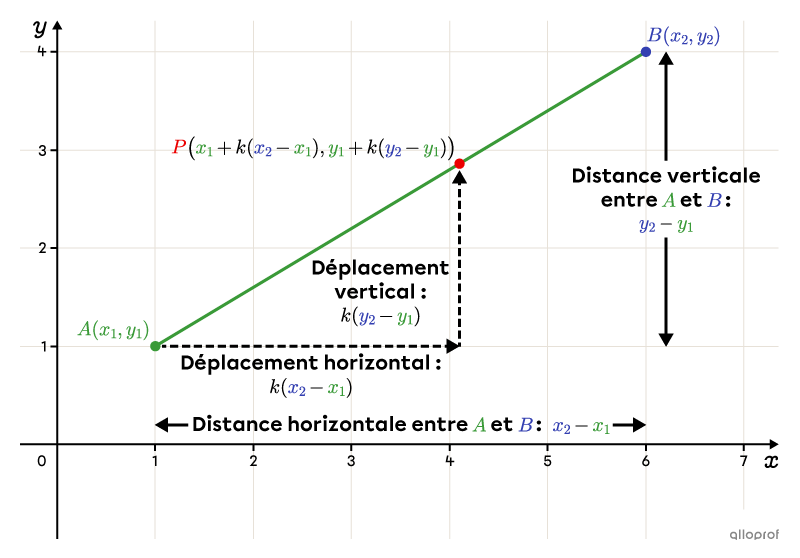
Il y a en quelque sorte 2 formules en une, soit celle pour l’abscisse du point de partage : |x_{\small{P}}=x_1+k(x_2-x_1)| et celle pour l’ordonnée : |y_{\small{P}}=y_1+k(y_2-y_1).|
Le raisonnement suivant permet d’expliquer le calcul de |x_{\small{P}}.|
-
|x_2-x_1| correspond à la distance horizontale entre les 2 extrémités du segment.
-
|k(x_2-x_1)| donne donc le déplacement horizontal qu’il faut effectuer à partir du point de départ |(A)| pour arriver au point |P.|
-
Comme l’abscisse du point de départ est |x_1,| on obtient bel et bien l’abscisse du point de partage |(x_{\small{P}})| en additionnant le déplacement horizontal à |x_1.|
Remarque : Le même raisonnement s’applique à |y_{\small{P}}.|
Parfois, la façon de partager le segment est donnée à l’aide d’un rapport de la partie au tout. D’autres fois, c’est à l’aide d’un rapport d’une partie à une autre partie. Lorsqu’on a déterminé de quel rapport il s’agit, on peut utiliser la formule du point de partage.
Soit le segment |\overline{AB}| suivant. Le point |P| partage ce segment en 2 parties |(\overline{AP}| et |\overline{PB}).| Ainsi, la longueur totale du segment correspond à la somme des parties |\overline{AP}| et |\overline{PB}.|
Le rapport de partage d’une partie au tout |\boldsymbol{(k)}|
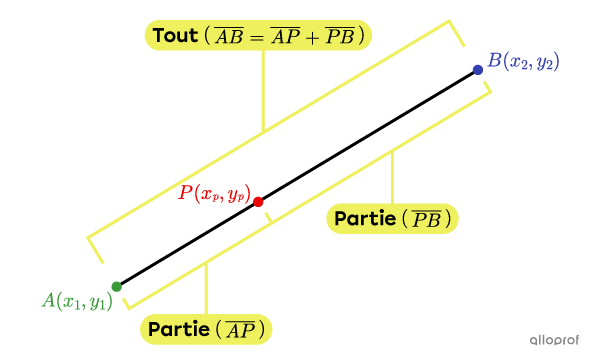
Lorsque le rapport selon lequel le point |P| sépare un segment est donné en comparant une partie du segment au segment en entier, on dit qu'il s'agit d'un rapport partie-tout. Ce rapport est toujours exprimé sous la forme d’une fraction.
Dans ce cas, il s’agit du rapport |\boldsymbol{k}| à utiliser dans la formule du point de partage. ||k=\dfrac{\text{m}\overline{AP}}{\text{m}\overline{AB}}||
Le rapport de partage d’une partie à une autre partie
Lorsque le rapport selon lequel le point |P| sépare un segment est donné en comparant les 2 parties du segment, on dit qu'il s'agit d'un rapport partie-partie.||\text{m}\overline{AP}\!:{\text{m}\overline{PB}}||Dans ce cas, la valeur du rapport |k| à utiliser dans la formule du point de partage est la suivante.||k=\dfrac{\text{m}\overline{AP}}{\text{m}\overline{AP}+\text{m}\overline{PB}}||
Il faut aussi porter une attention particulière au point de départ du segment, car cela a une incidence sur le rapport à utiliser |(k)| dans la formule du point de partage.
Parfois, le point de départ n’est pas donné explicitement. Par exemple, si on dit que |P| est situé aux |\dfrac{3}{10}| du segment |\overline{FG},| on doit tenir pour acquis que |F| est le point de départ.
Le rapport de partage d’une partie au tout |\boldsymbol{(k)}|
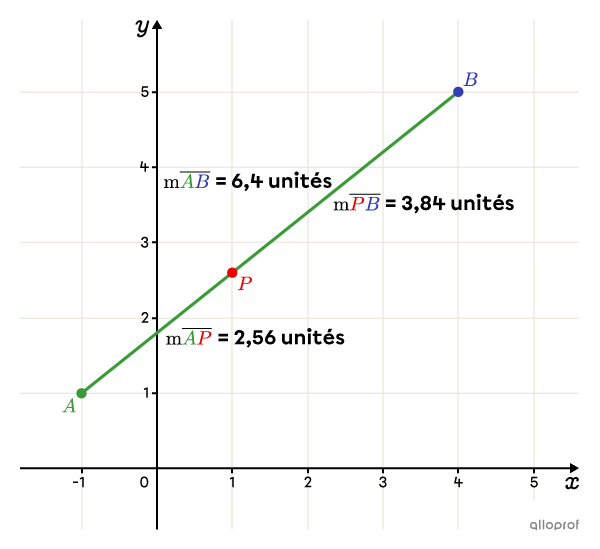
Le rapport partie-tout, exprimé à l’aide d’une fraction, est le suivant. ||\begin{align}k&=\dfrac{\text{m}\overline{AP}}{\text{m}\overline{AB}}\\[3pt] &=\dfrac{\text{m}\overline{AP}}{\text{m}\overline{AP}+\text{m}\overline{PB}}\\[3pt] &=\dfrac{2{,}56}{2{,}56+3{,}84}\\[3pt] &=\dfrac{2{,}56}{6{,}4}\\[3pt] &=\dfrac{2}{5}\end{align}||Autrement dit, le point de partage |(P)| est situé aux |\dfrac{2}{5}| du segment |\overline{AB}| à partir du point |A.|
Si on considère que |B| est le point de départ du segment |\overline{BA},| alors le point |P| est plutôt situé aux |\dfrac{3}{5}| du segment |\overline{BA}| à partir de |B.| En effet, |1-\dfrac{2}{5}=\dfrac{3}{5}.|
Le rapport de partage d’une partie à une autre partie
Le rapport partie-partie est le suivant. ||\text{m}\overline{AP}:\text{m}\overline{PB}=2{,}56:3{,}84||En simplifiant ce rapport, on obtient un rapport de |2:3.|
Autrement dit, pour |2| parts du segment |\overline{AP},| on retrouve 3 parts identiques sur le segment |\overline{PB}.|
On peut aussi dire que le point |P| partage le segment |\overline{BA}| dans un rapport de |3 : 2.|
Dans l'animation interactive suivante, tu peux déplacer le point de partage |\boldsymbol{\color{#ec0000}{P}}| et voir l’effet sur les 4 rapports possibles : le rapport partie-partie lorsque |A| est le point de départ et lorsque |B| est le point de départ, de même que le rapport partie-tout lorsque |A| est le point de départ et lorsque |B| est le point de départ.
Quelques exemples d’utilisation de la formule du point de partage
Soit les points |A(4,6)| et |B(8,12)|. On veut trouver les coordonnées du point |P| situé aux |\dfrac{3}{4}| du segment |\overline{AB}| à partir du point |A.|
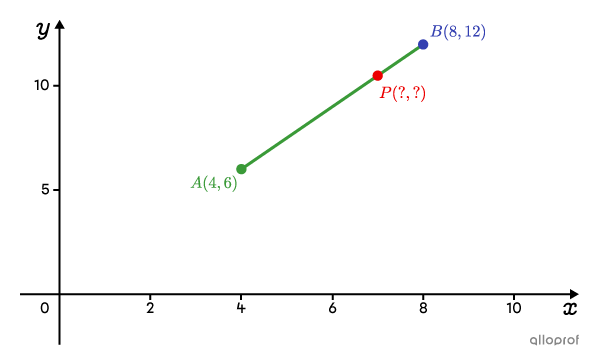
Ici, |(x_1,y_1)=(4,6)| et |(x_2,y_2)=(8,12).|
De plus, le rapport mentionné dans l'énoncé est un rapport de la partie au tout. Ainsi, |k=\dfrac{3}{4}| et le point de départ est le point |A.|
On peut donc appliquer la formule du point de partage. On peut l’appliquer d’un seul coup ou plutôt calculer séparément l’abscisse, puis l’ordonnée du point de partage. C’est ce qu’on va faire ici.
On débute donc en calculant l'abscisse du point |P,| qu'on note |x_{\small{P}}.| ||\begin{align} x_{\small{P}} &= x_1 + k(x_2-x_1)\\[3pt]&= 4 + \dfrac{3}{4}(8-4)\\[3pt]&= 4 + \dfrac{3}{4}(4)\\[3pt]&= 4 + 3\\[3pt] &= 7\end{align}||On calcule ensuite l'ordonnée du point |P,| qu'on note |y_{\small{P}}.| ||\begin{align} y_{\small{P}} &= y_1 + k(y_2-y_1)\\[3pt]&= 6 + \dfrac{3}{4}(12-6)\\[3pt]&= 6 + \dfrac{3}{4} (6)\\[3pt]&= 6 + 4{,}5\\[3pt] &= 10{,}5\end{align}||
Réponse : Le point de partage est |P(7; 10{,}5).|
Les extrémités d'un segment sont |A(5,-3)| et |B(10,6).| On veut trouver le point |P| situé dans un rapport |3:2| à partir du point |B.|
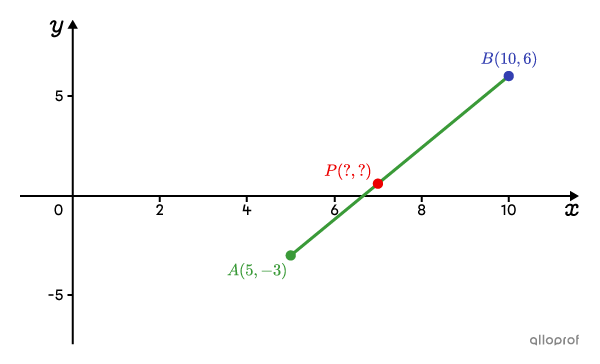
Le rapport mentionné dans l'énoncé est un rapport partie-partie. Il faut donc le transformer en rapport partie-tout.
Dans cet exemple, |\text{m}\overline{BP}:\text{m}\overline{PA}=3:2.| On calcule la valeur de |k| de la façon suivante.||k = \dfrac{3}{3+2} = \dfrac{3}{5}||Il faut aussi noter que le point de départ est le point |B| et non le point |A.| Ainsi, on doit utiliser la formule du point de partage avec |B(x_1,y_1)=(10,6)| et |A(x_2,y_2)=(5, -3).| ||\begin{align}(x_{\small{P}},y_{\small{P}})&=\big(x_1+k(x_2-x_1),\ y_1+k(y_2-y_1)\big)\\[3pt] &=\left(10+\dfrac{3}{5}(5-10),\ 6+\dfrac{3}{5}(-3-6)\right)\\[3pt] &=\left(10+\dfrac{3}{5}(-5),\ 6+\dfrac{3}{5}(-9)\right)\\[3pt] &=\left(10-3,\ 6-5{,}4\right)\\[3pt] &=\left(7; 0{,}6\right) \end{align}||
Réponse : Les coordonnées du point |P| sont donc |\left(7; 0{,}6\right).|
Si on connait le point de partage d’un segment ainsi qu’une des 2 extrémités, il est possible d’utiliser la formule du point de partage pour trouver les coordonnées de l’autre extrémité. Pour cela, il suffit de former une équation avec la coordonnée |x| et une autre avec la coordonnée |y.|
Dans le plan cartésien suivant, on retrouve les points |C,| |P(0,-3)| et |H(5,-12).| Ces 3 points sont alignés.
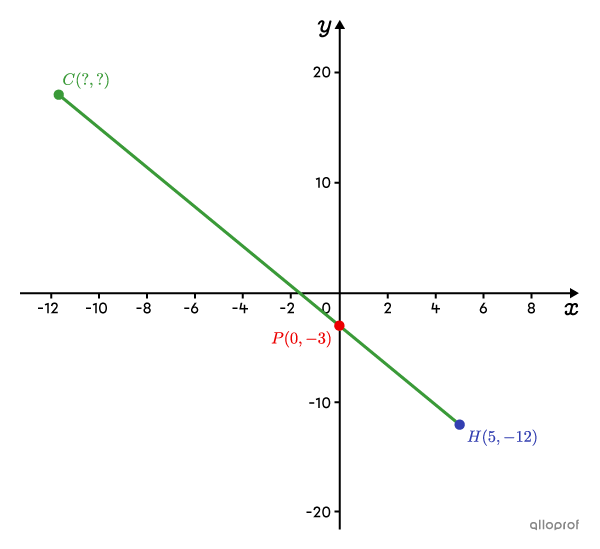
Le point |P| partage le segment |\overline{CH}| dans un rapport |7:3| à partir du point |C.|
Quelles sont les coordonnées du point |C|?
Le point de partage d'un segment - Exemple
Avant de commencer les calculs, il est important de noter que le rapport fourni est un rapport partie-partie. Il faut donc le transformer en rapport partie-tout.
Dans cet exemple, |\text{m}\overline{CP}:\text{m}\overline{PH}=7:3.| On calcule la valeur de |k| de la façon suivante.||k = \dfrac{7}{7+3} = \dfrac{7}{10}||Par conséquent, le rapport partie-tout est |k= \dfrac{7}{10},| où |C| est le point de départ.
On forme donc 2 équations : l’une avec les abscisses qui nous permettra de trouver la valeur de |x_1| et l’autre avec les ordonnées qui nous permettra de trouver |y_1.| On doit remplacer |x_{\small{P}}| et |y_{\small{P}}| par |0| et |-3,| de même que |k| par |\dfrac{7}{10}.| On remplace également |x_2| et |y_2| par les coordonnées de l’extrémité |H,| soit |5| et |-12| respectivement. Finalement, on résout les 2 équations.
||\begin{align} x_{\small{P}}&=x_1+k(x_2-x_1)\\[3pt]0&=x_1+\dfrac{7}{10}(5-x_1)\\[3pt] 0&=x_1+3{,}5-0{,}7x_1\\[3pt] \color{#ec0000}{\dfrac{\color{black}{-3{,}5}}{0{,}3}}&=\color{#ec0000}{\dfrac{\color{black}{0{,}3x_1}}{0{,}3}}\\[3pt] -\dfrac{35}{3}&=x_1\end{align}||
||\begin{align}y_{\small{P}}&=y_1+k(y_2-y_1)\\[3pt]-3&=y_1+\dfrac{7}{10}(-12-y_1)\\[3pt] -3 &=y_1-8{,}4-0{,}7y_1\\[3pt] \color{#ec0000}{\dfrac{\color{black}{5{,}4}}{0{,}3}}&=\color{#ec0000}{\dfrac{\color{black}{0{,}3y_1}}{0{,}3}}\\[3pt] 18&=y_1\end{align}||
Réponse : Les coordonnées du point |C| sont |\left(-\dfrac{35}{3},18\right).|
Remarque : Il est possible de considérer que le point de partage est situé aux |\dfrac{3}{10}| du segment |\overline{HC}| à partir du point |H,| car |\dfrac{10}{10}-\dfrac{7}{10}=\dfrac{3}{10}.| Dans ce cas, |k=\dfrac{3}{10},| |(x_1,y_1)=(5,-12)| et on recherche |(x_2, y_2).| Voici la preuve qu’on obtient la même réponse finale.
||\begin{align}x_{\small{P}}&=x_1+k(x_2-x_1)\\[3pt] 0&=5+\dfrac{3}{10}(x_2-5)\\[3pt] 0&=5+0{,}3x_2-1{,}5\\[3pt] -0{,}3x_2&=3{,}5\\[3pt] x_2&=\dfrac{3{,}5}{-0{,}3}\\[3pt] x_2&=\dfrac{-35}{3}\end{align}||
||\begin{align}y_{\small{P}}&=y_1+k(y_2-y_1)\\[3pt]-3&=-12+\dfrac{3}{10}(y_2--12)\\[3pt] -3&=-12+0{,}3y_2+3{,}6\\[3pt]-0{,}3y_2&=-5{,}4\\[3pt] -3y_2&=-54 \\[3pt]y_2&=18\end{align}||
Le point milieu d'un segment
||\text{Point milieu} = \left( \dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2} \right)||où
|(x_1,y_1)| et |(x_2,y_2):| les coordonnées des 2 extrémités d'un segment
Dans la formule du point de partage, il fallait faire |x_2| moins |x_1| et |y_2| moins |y_1,| alors que dans la formule du point milieu, il faut faire |x_1| plus |x_2| et |y_1| plus |y_2.|
En fait, il n’est même pas nécessaire de mémoriser la formule du point milieu. En effet, il suffit d’apprendre celle du point de partage, qui est plus polyvalente, et de remplacer |k| par |\dfrac{1}{2}.|
Quel est le point milieu du segment formé par les points |A(-2, 3)| et |B(1, 0)|?
||\begin{align} \text{Point milieu}&=\left(\dfrac{x_{1}+x_{2}}{2},\dfrac{y_{1}+y_{2}}{2}\right)\\[3pt]&=\left(\dfrac{-2+1}{2},\dfrac{3+0}{2}\right)\\[3pt]&=\left(-0{,}5; 1{,}5\right)\end{align}||
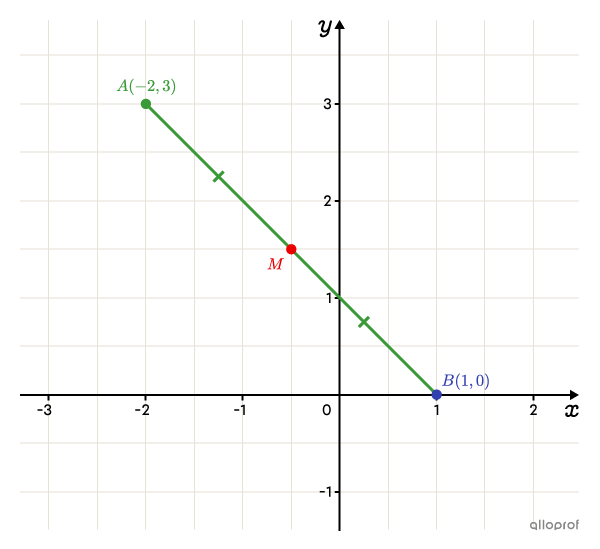
Si on connait le point milieu d’un segment ainsi qu’une des 2 extrémités, il est possible d’utiliser la formule du point milieu pour trouver les coordonnées de l’autre extrémité. Pour cela, il suffit de former une équation avec la coordonnée |x| et une autre avec la coordonnée |y.|
Les coordonnées du point milieu |(M)| du segment |\overline{CD}| sont |(12{,}5;-4).| Quelles sont les coordonnées du point |C| sachant que celles du point |D| sont |(8,1)|?
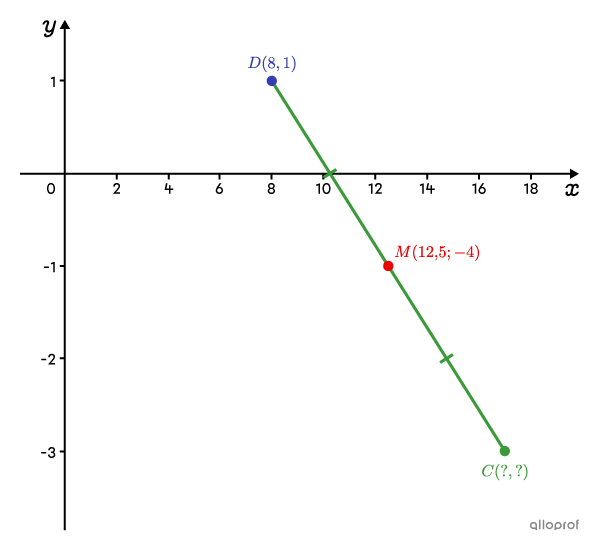
Dans la formule du point milieu, on remplace « point milieu » par les coordonnées |(12{,}5;-4).| On remplace également |x_2| et |y_2| par les coordonnées de l’extrémité |D,| soit respectivement |8| et |1.| ||\begin{align} \text{Point milieu}&=\left(\dfrac{x_{1}+x_{2}}{2},\dfrac{y_{1}+y_{2}}{2}\right)\\[3pt](12{,}5;-4)&=\left(\dfrac{x_1+8}{2},\dfrac{y_1+1}{2}\right)\end{align}||À partir d’ici, on forme 2 équations : l’une avec les abscisses qui nous permettra de trouver la valeur de |x_1| et l’autre avec les ordonnées qui nous permettra de trouver |y_1.| ||\begin{align}12{,}5&=\dfrac{x_1+8}{2}&-4&=\dfrac{y_1+1}{2}\\ 25&=x_1+8&-8&=y_1+1\\17&=x_1&-9&=y_1\end{align}||
Réponse : Ainsi, les coordonnées du point |C| sont : |(17,-9).|