Best Of
Re: Question
Bonjour XwingVirtuose1574,
Merci beaucoup pour ta question! Si tu juges que l’incertitude ne vaut pas la peine d’être respectée alors tu n’es pas obligé de la mettre dans ton graphique. Je suis d’accord avec toi, car c’est une très très petite incertitude. Voici une fiche qui pourrait t’aider :
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!
Re: Question
Bonjour FraiseAdorable5247,
Merci beaucoup pour ta question! Comme je te l’ai indiqué dans l’explication précédente, tu dois prendre le 0,25 (la moitié de 0,5).
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!
Re: Question
Bonjour FraiseAdorable5247,
Merci beaucoup pour ta question! En fait, l’incertitude d’un instrument de mesure correspond à la moitié de la plus petite graduation. Puisque la plus petite graduation de ton rapporteur d’angle est de 0,5 degré, ton incertitude est donc de 0,25 degré. Voici une fiche qui pourrait t’aider :
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!
Re: Question
Salut GalaxieArtistique6176!
Merci pour ta question. :)
En tant que tel, il n'y a pas d'erreur dans cette phrase, Peut-être que prise dans son contexte, le temps de verbe devrait être modifié!
Je te laisse cette fiche afin de valider le tout!
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane :)
Re: Question
Salut!
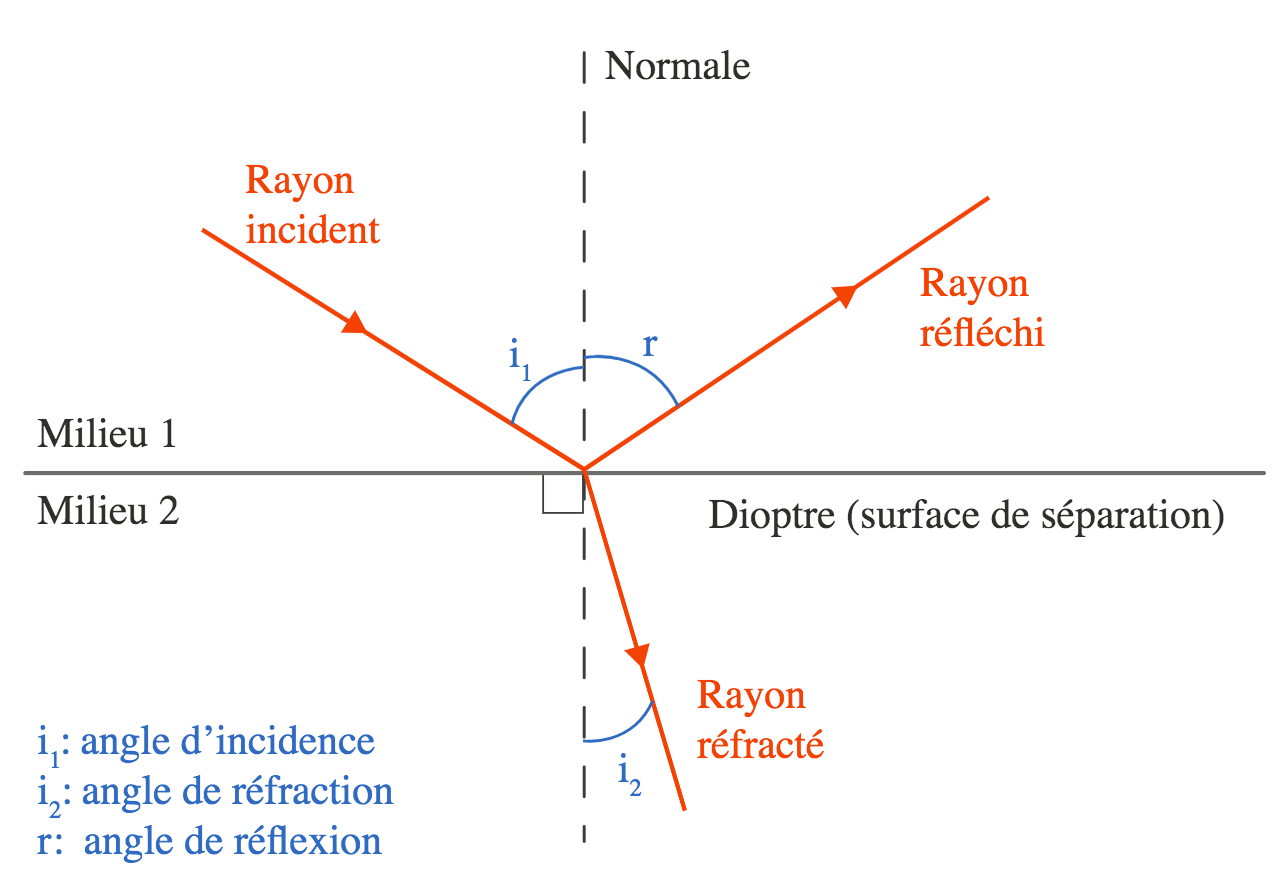
Le rayon réfléchi forme un angle de réflexion avec la normale.
On ne dit pas angle réfléchi, ni rayon de réflexion :)
Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Bonjour GirafeGamma1400,
Merci beaucoup pour ta question! Les gènes correspondent à des segments d’ADN dans lequel on retrouve de l’information génétique.
Pour leur part, les allèles sont les différentes formes que peuvent prendre les gènes. Chaque allèle occupe un endroit précis sur le chromosome.
Voici un exemple : les gènes pourraient correspondre à la couleur des yeux et les allèles seraient les yeux bleus ou les yeux bruns. Voici 2 fiches qui pourraient t’aider :
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!
Re: Question
Bonjour RenardMauve,
Merci de faire appel à nos services! :)
Les atomes sont les particules constituant les éléments. Les éléments sont les substances que tu retrouves dans le tableau périodique.
Les atomes peuvent se regrouper pour former des molécules comme pour les molécules d'eau qui sont formées de deux atomes d'hydrogène et un atome d'oxygène. D'où la formule H2O.
Pour en savoir plus, c'est juste ici :
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marilee
Re: Question
Bonjour FraiseAdorable5247,
Merci beaucoup pour ta question! À bien y penser, je suis d’accord avec l’explication que tu viens de me fournir. En effet, avec ce rapporteur d’angle, il est impossible de prendre une mesure avec 2 chiffres après la virgule. Cependant, il est possible de mesurer un angle avec une seule décimale. Je crois donc que tu peux écrire 0,0.
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!
Re: Question
Bonjour FraiseAdorable5247,
Merci beaucoup pour ta question! Selon moi, tu as eu raison de mettre 3 chiffres significatifs. En effet, d’habitude, il faut mettre autant de chiffres significatifs, que le chiffre le plus précis. Plus un chiffre comporte de nombres, plus le chiffre est précis. C’est pourquoi je crois que tu as raison dans ton explication! Voici une fiche qui pourrait t’aider :
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!