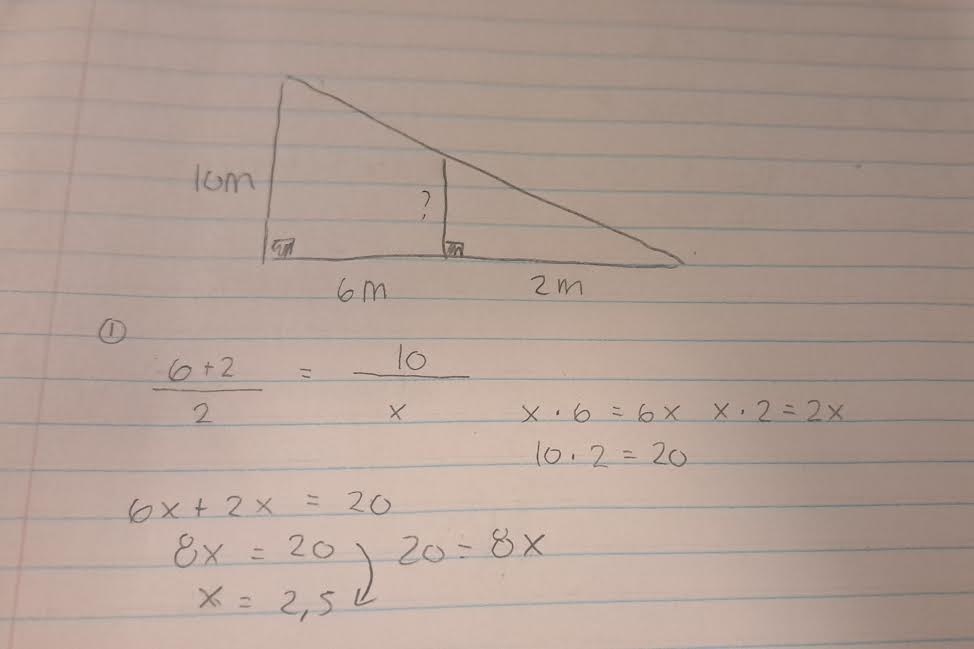Best Of
Re: Question
De se que j'ai trouver non. Il représente seulement 80% des gaz à effet de serre.
Re: Question
Salut!
Tu peux commencer par trouver combien de dollars canadiens sont nécessaires pour avoir 100$ américains sachant que 0,91 $ canadien = 1 dollar américain. Tu dois donc résoudre cette proportion :
$$ \frac{0,91$ ~canadien}{1$ ~américain} = \frac{?$~ canadien}{100$ ~américain}$$
Ensuite, tu dois trouver le nombre d'euros pour avoir ce montant de dollars canadiens sachant que 1,25 $ canadien = 1 euro.
Je te laisse essayer avec ces indices. N'hésite pas à nous réécrire si tu as besoin d'un coup de main supplémentaire! :)
Re: Question
Tu peux l'identifier lorsque tu remarque qu'il guide le mouvement d'autres pièces. (L'aide à accomplir un mouvement de translation, de rotation ou hélicoïdal).
Par exemple, une glissière comme dans un tiroir ou un pivot comme sur des ciseaux. (En secondaire 3 tu verras un peu mieux les types de guidages mais pour l'instant, tu peux te concentrer sur le fait que celui-ci guide le mouvement).
J'espère t'avoir aidé.e!
Re: Question
Hello !
Thank you for your question !
You can find your missing height by making a similar triangle since you have a small triangle in a large triangle.
To do this you do : Big side of the triangle/ small side of the triangle
Attention: very important to calculate the good sides between them.
Do not hesitate if you have other questions !
BrachiosaureTimide314
Re: Question
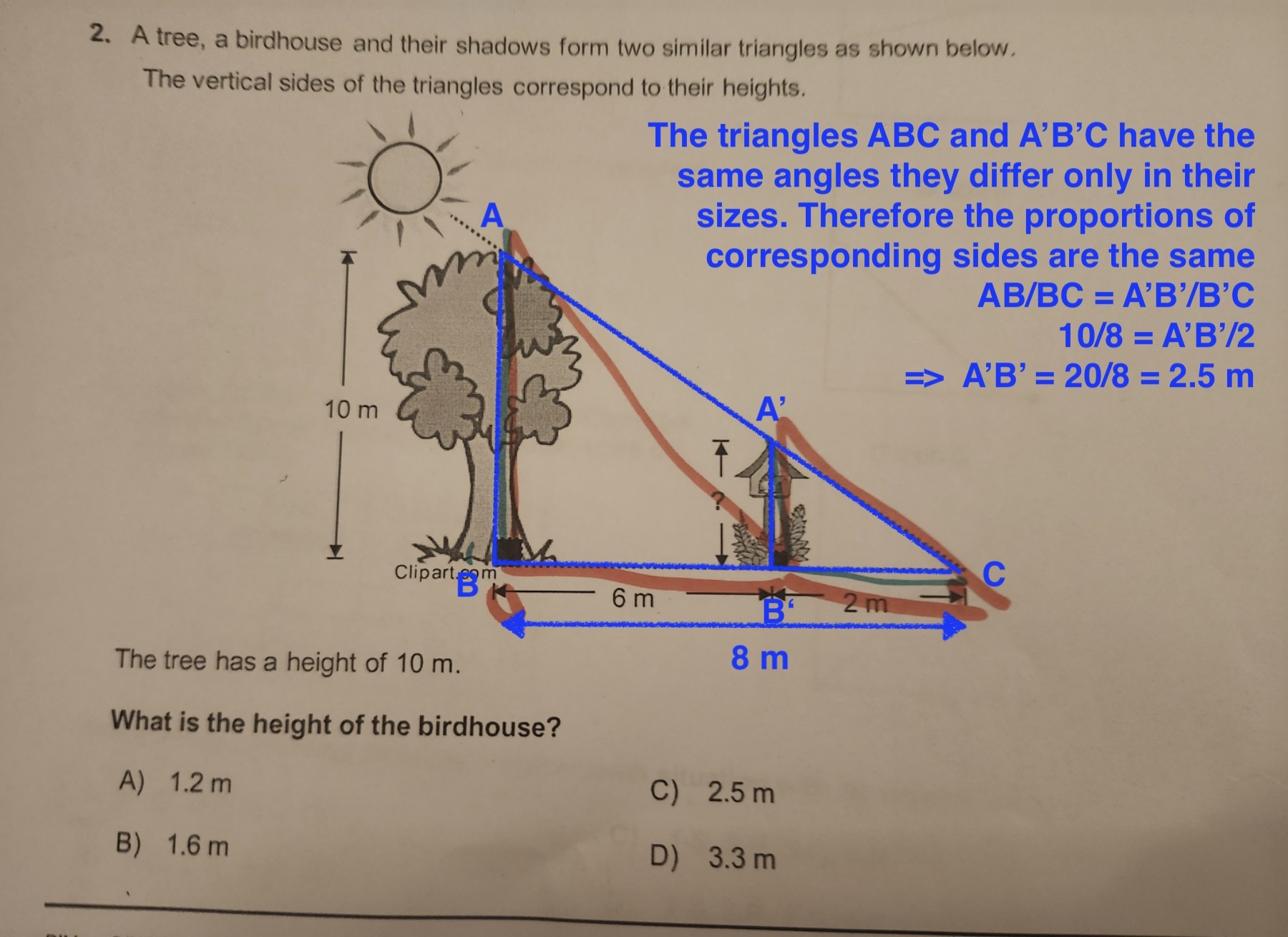
Hi! So when you have two similar shapes it means that the measures of each side of both figures are proportional. So here, you can see that the base of the big triangle measure 8cm (6+2), and the base of the small triangle is 2cm. What you do is you divide 8 by 2, which is 4. So it means that when you multiply a side of the small triangle by 4, you get the measure of that same side but for the big triangle. So here you need the height of the small triangle but you already have the height of the big triangle, so you do the opposite and you divide 10 by 4 and you get 2,5cm
I hope this helps!😃
Re: Question
le gouvernement canadien ont offert des terres gratuites et prometant de payer le trajet du bateau. il ont été transmit par des agent d'immigration afin d'inviter des eurropeens, etc.
Tout cela a causé un surplus de popalatio,ce qui a mené le deplacment vers l'Ouest du Canada créant deux provinces; la Saskatchewan et l'Alberta
j'éspère que mon explication t'a aider et qu,elle n'est pas trop en retard.
Re: Question
Salut!
Un ion monoatomique est un ion formé à partir d'un seul atome (exemples : \(K^+\), \(Na^+\)), tandis qu'un ion polyatomique est un ion formé de plusieurs atomes (exemple \(NH_4^+\) ).
J'espère que c'est plus clair pour toi! :)
Re: Question
Salut!
Tu dois commencer par simplifier l'expression en annulant le signe négatif au dénominateur, comme ceci :
$$ \frac{7x-5}{-2(x+3)}$$
$$ -\frac{7x-5}{2(x+3)}$$
$$ \frac{-7x+5}{2(x+3)}$$
Puis, tu dois distribuer le facteur 2 à l'intérieur de la parenthèse. Ensuite, tu devras diviser le numérateur par le dénominateur avec la méthode de la division par crochet. Consulte cette fiche au besoin : La division d'une expression algébrique par un binôme | Secondaire | Alloprof
Tu peux également consulter la section "passage de la forme P/Q à la forme canonique" de la fiche suivante, elle présente justement la démarche pour passer d'une équation de 4 paramètres à une équation de 3 paramètres : Le passage de canonique à générale pour la fonction rationnelle | Secondaire | Alloprof
Je te laisse essayer avec ces indices. N'hésite pas à nous réécrire si tu as besoin d'un coup de main supplémentaire! :)