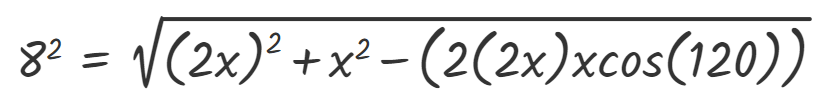Best Of
Re: Question
Bonjour, MoustiqueNoble9961,
Merci de solliciter nos services.
Les substances acides et basiques sont constructrices d’électricité puisqu’elles sont chargées positivement ou négativement.
Toutefois, les substances neutres sont des substances contenant autant de charges positives que de charges positives, donc, selon toi, une substance neutre peut-elle être conductrice d’électricité ?
N’hésite pas à nous réécrire si tu as d’autres questions!
À bientôt !
Émilie
Re: Question
Salut à toi!
Merci pour ta question :)
En fait, pour y répondre, on a besoin de connaître les positions relatives de deux droites:
Comme tu peux voir sur ce tableau, la forme qu'on t'a donnée semble être la forme mentionnée sous la forme générale perpendiculaire. On devrait donc la transformer en forme générale!
On a donc fait a multiplié par x et b multiplié par y pour annuler la division, et le c a plutôt été mis de l'autre côté de l'égalité, ce qui nous donne 1! Le symbole négatif est causé par l'orientation perpendiculaire de la droite.
Pour en apprendre plus sur la position relative de deux droites, c'est par ici:
J'espère que ça répond à ta question!
Bonne soirée :)
Ariane
Re: Question
Bonjour DauphinAdmirable9337,
Tu as bien identifier les côtés AB et BC. Tu devras utiliser la loi des cosinus avec la variable ''x''. Il te faudra résoudre l'équation pour isoler ''x'' et après substitution, il te restera à calculer la périmètre de ton triangle en faisant la somme des 3 côtés.
P.S. Étant donné qu'il y a des exposants 2, il se peut que tu aies à utiliser la formule quadratique pour trouver la (les) valeur(s) possible(s) de x.
Bon travail
Re: Question
Bonjour DragonFiable418,
Merci d'avoir choisi d'utiliser la zone d'entraide pour répondre à votre question!
Tout d'abord, l'héliotropisme est la capacité d'une plante de se tourner vers le soleil afin d'absorber les rayons (la lumière) dont chaque plante a de besoin pour faire la photosynthèse. Ce n'est pas la même chose que le phototropisme où la plante pousse dans la direction du soleil. L'héliotropisme est simplement la maximisation de l'espace occupée par la plante en se tournant vers le Soleil. Bien sûr, la plante pourra après se retourner si elle le veut.
Voici une fiche de Futura-sciences pour vous aider à comprendre.
Héliotropisme: Définition | Héliotropisme (futura-sciences.com)
J'espère que j'ai pu répondre à votre question!
N'hésitez pas de demander d'autres questions si vous voulez.
Bonne chance et bonne lecture!
Question
Bonjour! J'ai une examen qui s'en vient (étude de cas). Je voudrais savoir ce sont quoi les systèmes (en ordre) de la Tendinite et expliquez pourquoi. Merci de répondre et passez une belle journée!!
Re: Question
Bonjour, RubisRouge730,
Merci de solliciter nos services.
Afin de tout connaitre concernant Darwin et la sélection naturelle, je t’invite à cliquer sur le lien ci-dessous.
N’hésite pas à nous réécrire si tu as d’autres questions ou si tu as besoin de précisions!
À bientôt !
Émilie
Re: Question
Bonjour GalaxieTurquoise,
Merci de faire appel à nos services! :)
Quand un enseignant donne la consigne « de répondre avec un texte suivi », il veut que tu écrives un texte qui se suit. Par exemple, tu ne dois pas écrire une « liste d’épicerie » composée de phrases sans lien entre elles.
Exemple de réponse en texte non suivi :
Le personnage est triste parce que :
- La mère du personnage est décédée
- Le personnage a perdu son emploi.
- Il est seul.
Exemple de réponse en texte suivi :
Le personnage est triste pour diverses raisons. D’abord, il vit une grande solitude depuis que sa mère est morte et qu’il n’a pas d’autres proches. La plupart du temps, il est donc seul, ce qui l’affecte considérablement. De plus, il mentionne dans le livre qu’il n’a jamais été seul auparavant ; il est donc très déstabilisé. Ensuite, le personnage a perdu son emploi. Il ne reçoit plus de revenus, ce qui le stresse beaucoup…
En ce sens, il existe divers types de textes pouvant être considérés comme des textes suivis, chacun ayant une structure distincte:
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marilee
Re: Question
Bonjour ElfeOptimiste,
Merci de faire appel à nos services! :)
En fait, la substance blanche est composée principalement de faisceaux d'axones, qui sont des prolongements des neurones. Ces axones sont entourés d'une substance grasse appelée myéline, ce qui donne à la substance blanche sa couleur. Au microscope, tu verrais donc beaucoup de fibres longues et brillantes.
La substance grise contient surtout les corps cellulaires des neurones, ainsi que leurs dendrites et les synapses (les connexions entre les neurones). Au microscope, tu verrais des cellules nerveuses (les neurones) avec des noyaux distincts, des dendrites et un environnement moins fibreux comparé à la substance blanche.
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marie-France