Best Of
Re: Question
Merci pour ta question!
L'essentiel des problèmes de projectile lancée en oblique est de savoir décomposer le mouvement en deux composantes. En effet, le tout devient beaucoup plus simple lorsqu'on reconnait qu'il y a un mouvement horizontal et vertical.
En général, le mouvement horizontal est un mouvement rectiligne uniforme. En effet, peu de problèmes de physique demandent de tenir compte de la résistance de l'air. Ainsi, tu peux assumer que ce mouvement suit la trajectoire suivante :
$$ x_t = x_i+v_i•t $$
Légende :
• xt : position horizontale à l’instant t (m)
• xi : position horizontale initiale (m)
• vi : vitesse horizontale initiale (m/s)
• t : temps (s)
Le mouvement vertical est plutôt un mouvement rectiligne uniformément accéléré. Ainsi, il faut le modéliser comme suit :
$$ y_t = y_i+v_i•t+\frac{1}{2}•a•t^2 $$
Légende :
• yt : position verticale à l’instant t (m)
• yi : position verticale initiale (m)
• vi : vitesse verticale initiale (m/s)
• t : temps (s)
• a : accélération (m/s^2)
Souvent, tu peux assumer que la gravité = 9,81 m/s^2 car les problèmes sont sur Terre.
Une deuxième stratégie est de bien lire la question pour trouver les valeurs des variables. En effet, parfois, il semble manquer de données, mais ce n'est en réalité car les informations sont inscrites dans la question. Par exemple, si l'objet est «immobile au départ», c'est que sa vitesse initiale est de 0.
Puis, l'ordre des calculs est important; par exemple, il faut parfois savoir le temps pendant lequel un objet tombe avant de calculer le déplacement horizontal, car ce dernier nécessite de connaitre la durée du mouvement.
Finalement il est utile de connaitre d'autres formules de la cinématique, comme celle de la vitesse selon le temps :
$$ v_t = v_i+a•t $$
Légende :
• vt : vitesse à l’instant t (m)
• vi : vitesse initiale (m)
• a : accélération (m/s^2)
• t : temps (s)
Cette dernière est particulièrement utile lorsqu'il faut calculer la vitesse finale verticale d'un objet.
Cette fiche du site d'Alloprof explique la cinématique :
N'hésite pas si tu as d'autres questions!
Re: Question
Merci pour ta question! 😊
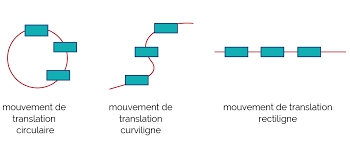
Une translation curviligne est une translation qui ne va pas dans une ligne droite, mais qui suit plutôt le trajet d'une courbe.
N'hésite pas si tu as d'autres questions!
Question
Bonjour! J'ai fait quelques recherches, mais je suis incapable de trouver une réponse claire sur la question suivante :
Pourquoi le Canada et les États-Unis ne reconnaissent pas l'indépendance de la Palestine?
Merci et bonne fin de journée :)
Re: Question
Bonjour FraiseComique,
Merci de faire appel à nos services! :)
Un verbe essentiellement pronominal s'emploie uniquement à la forme pronominale, donc avec l'utilisation de deux pronoms personnels de la même personne ainsi que de l'auxiliaire être.
Par exemple, le verbe s'évanouir est essentiellement pronominal, puisqu'on ne peut pas l'utiliser avec seulement un pronom personnel, on ne peut pas dire «elle évanouit».
Un verbe occasionnellement pronominal est un verbe transitif qui peut être utilisé autrement qu'à la forme pronominale.
Par exemple, le verbe parler peut être utilisé avec un et deux pronoms personnels. Nous pouvons dire «je parle» et «je me parle».
Je te laisse un lien provenant de notre site qui aborde le verbe pronominal, si tu souhaites réviser cette notion:
Le participe passé d’un verbe essentiellement pronominal s’accorde en genre et en nombre avec le pronom ou le groupe de mots qui occupe la fonction de sujet du verbe.
Ex. :
- Mariana s’est absentée du dernier tournoi d’échecs.
Le verbe s’absenter est essentiellement pronominal. Le participe passé absentée s’accorde donc en genre et en nombre avec le groupe nominal (GN) Mariana (féminin, singulier), qui occupe la fonction de sujet.
--------
Le participe passé d’un verbe occasionnellement pronominal (parfois appelé accidentellement pronominal) s’accorde en genre et en nombre avec le pronom ou le groupe de mots qui occupe la fonction de complément direct (CD) s’il est placé avant le verbe.
S’il n’y a pas de complément direct ou que ce dernier est placé après le verbe, le participe passé ne s’accorde pas.
Ex. :
- Édouard et Enola se sont découragés en voyant la pile de vaisselle qui les attendait.
Dans cette phrase, le complément direct est le pronom personnel conjoint se, qui est du même genre et du même nombre que le sujet, soit le groupe nominal Édouard et Enola. Comme ce pronom est placé avant le verbe, le participe passé découragés s’accorde en genre et en nombre avec ce dernier (masculin, pluriel).
Voilà! N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marilee
Question
Quelles sont les réalisation de James McGill et comment à t'il fait pour fonder l'Université de McGill?
Re: Question
Bonjour DragonExemplaire,
Merci de faire appel à nos services! :)
C'est très gentil de vouloir aider ta petite soeur! Voici quelques trucs que tu peux faire pour l'aider :
Lire en écho
Pour permettre à ta soeur de gagner en fluidité, tu peux lui proposer de lire en écho avec toi. Pour y arriver, tu dois :
- choisir un livre;
- lire la première phrase à haute voix;
- inviter ta soeur à lire à haute voix la même phrase que vous, immédiatement après vous;
- répéter l’exercice pour chaque phrase.
Lire à l'unisson
Cette activité, qui peut être aussi bénéfique que rigolote, est très facile à mettre en place. Il suffit de:
- choisir un livre;
- lire en simultané la même phrase que ta soeur;
- relire la même phrase plusieurs fois, jusqu’à ce que sa lecture soit fluide;
- répéter l’expérience pour chaque phrase.
Pour connaitre d'autres trucs, je t'invite à consulter la fiche suivante :
Elle s'adresse aux parents, mais les trucs qui y sont donnés peuvent être utilisés par n'importe qui! :)
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marilee
Re: Question
Salut !
Je t'invite à consulter ces liens, des questions très similaires à la tienne ont déjà reçu des explications :)
N'hésite surtout pas à nous réécrire si tu as d'autres questions! :)
Re: Question
Salut!
Pour résoudre une inéquation et trouver l'inconnu, tu dois toujours placer les termes semblables d'un côté de l'inéquation, et les constantes de l'autre côté
$$ \frac{x}{2} +4 < - x -5 $$
Les termes semblables sont les termes ayant les mêmes variables (les mêmes inconnus), et ces variables sont affectées des mêmes exposants. Donc, nos termes semblables sont ici x/2 et -x, puisqu'ils contiennent tous les deux la variable x affectée d'un exposant 1.
Les constantes sont les termes qui ne contiennent pas de variables, soit ici 4 et -5.
Notre but sera d'abord de placer d'un côté de l'inégalité les deux termes semblables, et de l'autre côté les constantes. Pour ce faire, nous allons commencer par déplacer un des deux termes semblables de l'autre côté (peu importe lequel), et ce, en effectuant l'opération inverse.
Déplaçons -x du côté gauche de l'inégalité. Puisque l'opération inverse d'une soustraction est une addition, nous allons devoir additionner x de chaque côté de l'inéquation, comme ceci :
$$ \frac{x}{2} +4 +x< - x -5+x $$
En le soustrayant de chaque côté, cela nous permet de l'éliminer du côté droit de l'inéquation :
$$ \frac{x}{2} +4 +x< -5 $$
On a ainsi déplacé le terme \(x\) afin qu'il soit du même côté que son terme semblable.
Passons maintenant aux constantes. Nous allons déplacer la constante 4 de l'autre côté. Puisque l'opération inverse d'une addition est une soustraction, nous allons donc soustraire 4 de chaque côté :
$$ \frac{x}{2} +4 +x-4< -5-4 $$
$$ \frac{x}{2} +x< -5-4 $$
On a ainsi réussi à placer nos termes semblables d'un côté et nos constantes de l'autre! La prochaine étape sera d'additionner les constantes, et d'additionner les coefficients des termes semblables. Commençons par les constantes. Puisque -5-4 donne -9, nous avons
$$ \frac{x}{2} +x< -9 $$
Pour additionner les termes semblables, il faut additionner leur coefficient, c'est-à-dire le nombre devant la variable x.
$$ \frac{1}{2}x +(1)x< -9 $$
$$ (\frac{1}{2}+1)x< -9 $$
$$ (\frac{1}{2}+\frac{2}{2})x< -9 $$
$$ (\frac{1+2}{2})x< -9 $$
$$ \frac{3}{2}x< -9 $$
Finalement, la dernière étape sera d'éliminer le coefficient de la variable x, soit 3/2, et ce, en effectuant l'opération inverse d'une multiplication, soit une division :
$$ \frac{3}{2}x \div \frac{3}{2}< -9\div \frac{3}{2} $$
$$ x< -9\div \frac{3}{2} $$
$$ x< -9\times \frac{2}{3} $$
$$ x< - \frac{9\times2}{3} $$
$$ x< - \frac{18}{3} $$
$$ x< - 6$$
Voilà! Voici des fiches sur ces notions qui pourraient t'être utiles :
- La résolution d'équations et d'inéquations | Secondaire | Alloprof
- Algèbre - Expressions algébriques | Alloprof
J'espère que c'est plus clair pour toi! Sinon, n'hésite pas à nous réécrire! 😁
PS Si tu as un appareil mobile ou une tablette, tu peux utiliser l'application Photomath pour t'aider dans tes résolutions d'inéquations!