Best Of
Re: Question
Bonjour LuneRouge,
Merci pour ta question!
La neutralisation acido-basique est la réaction entre un acide et une base, ce qui les "annule" et forme un sel et de l'eau.
Pour plus d'explications et des exemples:
N'hésite pas si tu as encore besoin d'aide:)
Kylan
Re: Question
Hello, ResponsibleDiamond220!
To switch to the symmetrical form from the general form -2x+7y-3=0, transform the equation so it is equal to 1.
First, move the 3 to the other side of equality.
$$ \begin{align} -2x+7y-3&=0\\ -2x+7y-3+3&=+3\\ -2x+7y&=3\\ \end{align}$$
Second, the equality must be equal to 1. Thus, divide the terms by 3.
$$ \frac{-2x}{3}+\frac{7y}{3}=\frac{3}{3}\\ $$
Third, after simplifying, the result is:
$$ \frac{-2x}{3}+\frac{7y}{3}=1 $$
This is not yet in symmetrical form.
However, it is possible to express it in symmetric form by inverting the coefficients of x and y and placing them in the denominator.
$$ \frac{x}{-\frac{3}{2}}+\frac{y}{\frac{3}{7}}=1 $$
Do not hesitate to contact us if you have other questions!
Re: Question
Bonjour DragonHumoristique7584
Merci d'avoir utilisé la zone d'entraide pour répondre à ta question.
Pour ta première question, œil au pluriel est yeux.
Ensuite, dans le cas de la conjonction « mais », on place souvent la virgule avant celle-ci. Voici une fiche sur les conjonctions qui pourrait t'aider:
J'espère que j'ai répondu à tes questions!
Re: Question
Bonjour, MentheGamma4453!
Premièrement, on isole le rapport cosinus.
$$\begin{align} 4\cos(x)+2&=0\\ \cos(x)&=-\frac{2}{4}\\ \cos(x)&=-\frac{1}{2}\\ \end{align} $$
Deuxièmement, on détermine les angles trigonométriques.
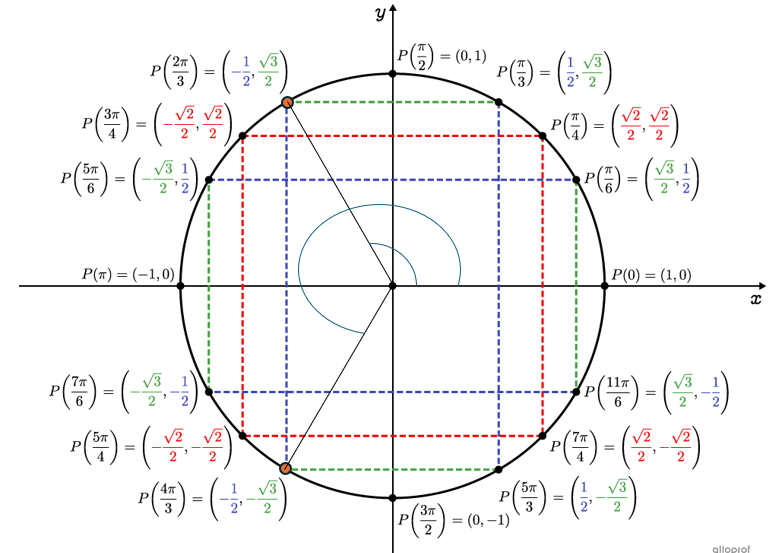
Puisque -1/2 est une abscisse de points remarquables, on détermine les angles recherchés directement à partir du cercle trigonométrique.
On trouve que les angles pour lesquels l’abscisse vaut -1/2 sont 2π/3 et 4π/3.
Troisièmement, on résout l'équation.
$$\begin{align}\cos(x)&=-\dfrac{1}{2}\\&\Downarrow\\x&=\dfrac{2\pi}{3}\\[3pt]\boldsymbol{\color{#fa7921}{x_1}}&=\boldsymbol{\color{#fa7921}{\dfrac{2\pi}{3}}}\end{align}$$
$$\begin{align}\cos(x)&=-\dfrac{1}{2}\\&\Downarrow\\x&=\dfrac{4\pi}{3}\\[3pt]\boldsymbol{\color{#51b6c2}{x_2}}&=\boldsymbol{\color{#51b6c2}{\dfrac{4\pi}{3}}}\end{align}$$
Quatrièmement, on calcule la période de la fonction cosinus pour être en mesure de donner toutes les solutions.
$$ p=\dfrac{2\pi}{\vert b\vert} $$
Cinquièmement, on donne les solutions de l'équation.
Dépendemment de l'intervalle, on soustrait ou additionne la période aux 2 solutions trouvées.
Je te laisse consulter la fiche explicative pour plus de détails.
N'hésite pas à nous contacter si tu as d'autres questions!
Re: Question
Bonjour BrachiosaureTimide314
Merci d'avoir utiliser la zone d'entraide pour répondre à ta question.
Le mot guerre, dans Guerre froide, doit être mis en majuscule. Voici le lien d'un site qui t'expliquera pourquoi en profondeur:
J'espère que j'ai répondu à ta question!
Re: Question
Salut CygneEmpathique9274,
Merci pour ta question!
Malheureusement, nous n'avons pas d'exercice sur la solubilité. Par contre, nous avons une fiche à ce sujet qui peut t'aider :
Je t'invite à la lire, il s'agit d'une bonne révision!
J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions!
Anthony B.
Question
Est-ce que Les astéroïdes qui sont attiré par Le Soleil sont liés à la gravitation universelle?
Question
Une solution a une concentration de 0,773g/l. Quelle est la concentration de cette solution en ppm?