Best Of
Re: Question
Salut LibelluleMagnifique3765 !
Merci pour ta question. :)
Les torticolis sont souvent le résultat d'une blessure non traitée. N'importe quel petit mouvement peut donc être à l'origine d'un torticolis (bouger la tête, par exemple).
Pour s'en débarrasser, la chaleur peut être efficace (sac magique, bouillotte), les étirements du cou également, mais je suggère tout de même de consulter un professionnel !
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau !
À bientôt,
Océane :)
Re: Question
Bonjour CitronJaune4169,
Merci beaucoup d’avoir utiliser la zone d’entraide.
Si tu parles du jeu Magimot, il est supposé être pour les élèves de deuxième année du primaire jusqu’à la sixième année du primaire.
Toutefois, puisque tu peux choisir les mots que tu veux pratiquer, je pense que ça serait correct d’utiliser le jeu lors de ta première année du secondaire si tu as de la difficulté à retenir l'orthographe de certains mots.
J’espère t’avoir aidé. Bonne chance et n’hésite pas à revenir nous voir quand tu en as besoin!
DauphinInsolite7158
Question
C’est quoi la différence entre une droite, une demi droite et un segment?
Re: Question
Salut!
Une droite est une ligne qui s'étend à l'infini dans les deux sens.
Une demi-droite commence à un point et s'étend à l'infini dans une seule direction.
Un segment est une portion finie d'une droite, délimitée par deux points qui sont les extrémités du segment. Le segment a une longueur déterminée et ne s'étend pas à l'infini.
Je t'invite à consulter la fiche suivante : Les sortes de lignes | Secondaire | Alloprof
Et à revenir nous voir si tu as d'autres questions! :)
Re: Question
Bonjour TitaneEnthousiaste3913
Merci beaucoup d'avoir utilisé la zone d'entraide pour t'aider.
Dans ce problème, tu dois trouver la règle de la fonction. Voici une fiche qui pourrait t'aider à trouver celle-ci en fonction des éléments retrouvés dans ton problème !
J'espère t'avoir aidé.
GobelinOrange154
Re: Question
Salut 😁
Bien sûr!
Voici d'abord les fiches sur le sujet.
Solides troués (ils sont ici classés dans les solides décomposables, car le trou peut être considéré comme un solide qu'on enlève)
Solides tronqués + Solides décomposables
Ensuite, quelques astuces concernant les types de solides que tu as.
Pour les solides qui ont des trous, on soustrait le volume du trou au volume total du solide, ce qui donne le volume du solide plein.
Pour les solides décomposables, il faut additionner les différents volumes des solides que tu as (ex. : une sphère + prisme rectangulaire).
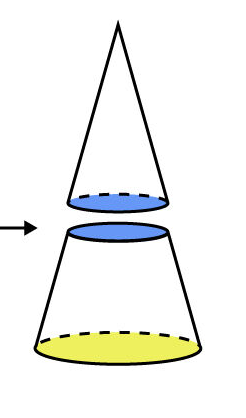
Pour les solides tronqués, il faut combiner les additions et des soustractions afin de trouver la bonne formule à utiliser.
Si on a le solide suivant et qu'on cherche l'aire, on devra mettre une fois l'aire latérale du cône complet (car, si on le colle, ça donne toute la surface) + Aire de la base jaune + Aire des deux surfaces en bleu.
N'hésite pas si tu as d'autres questions 😊 À bientôt 😎
Re: Question
Salut OkapiAlpha4705 !
Merci pour ta question. :)
Je t'invite à consulter cette fiche pour obtenir nos meilleurs trucs pour s'améliorer en compréhension de lecture !
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau !
À bientôt,
Océane :)
Question
bonsoir, puis-je avoir des exemples de phrases qui rime s'il vous plaît.
Merci !
Re: Question
Bonjour GirafeArtistique1717!
Merci d'utiliser la Zone d'Entraide pour poser ta question.
Voici différents moyens de gérer ton stress:
1-Avoir une balle antistress en classe (si ta/ton prof le permet).
2-Prendre 3 grandes inspirations dans les moments de stress, comme avant un oral ou un examen.
3-Allez faire de sport.
4-Prendre des bains de forêt (pas littéralement, cela veut simplement dire de prendre une marche en forêt)
J'espère t'avoir aidé,
ArsenicBeta2097