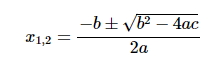Best Of

Salut!

Nous n'avons pas de fiche sur cette notion malheureusement, puisqu'il s'agit d'une notion couverte au collégial uniquement. Cependant, voici deux vidéos introduisant le sujet qui pourraient t'intéresser :

• LE COURS : La dérivation - Première - YouTube
• Calcul Différentiel Dérivée - CEGEP au Québec - YouTube

Bon visionnage! :)

Grosso modo, c'est la pente d'une fonction f(x) en un point particulier x.

Pour la droite, c'est simple, la pente est constante.

Pour une parabole à l'envers par exemple, la pente (dérivée) est positive au début, elle diminue en approchant du sommet, au sommet elle est nulle, puis elle devient négative après le sommet.

C'est quand même très avancé. Les sites mentionnés par Katia sont sans doute très appropriés, en voici un autre:

https://progresser-en-maths.com/derivation/

En général on étudie les limites avant de s'attaquer aux dérivées.

Je ne comprends pas bien ce problème…

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Re salut!

Contente que mon explication t'ait été utile! :D

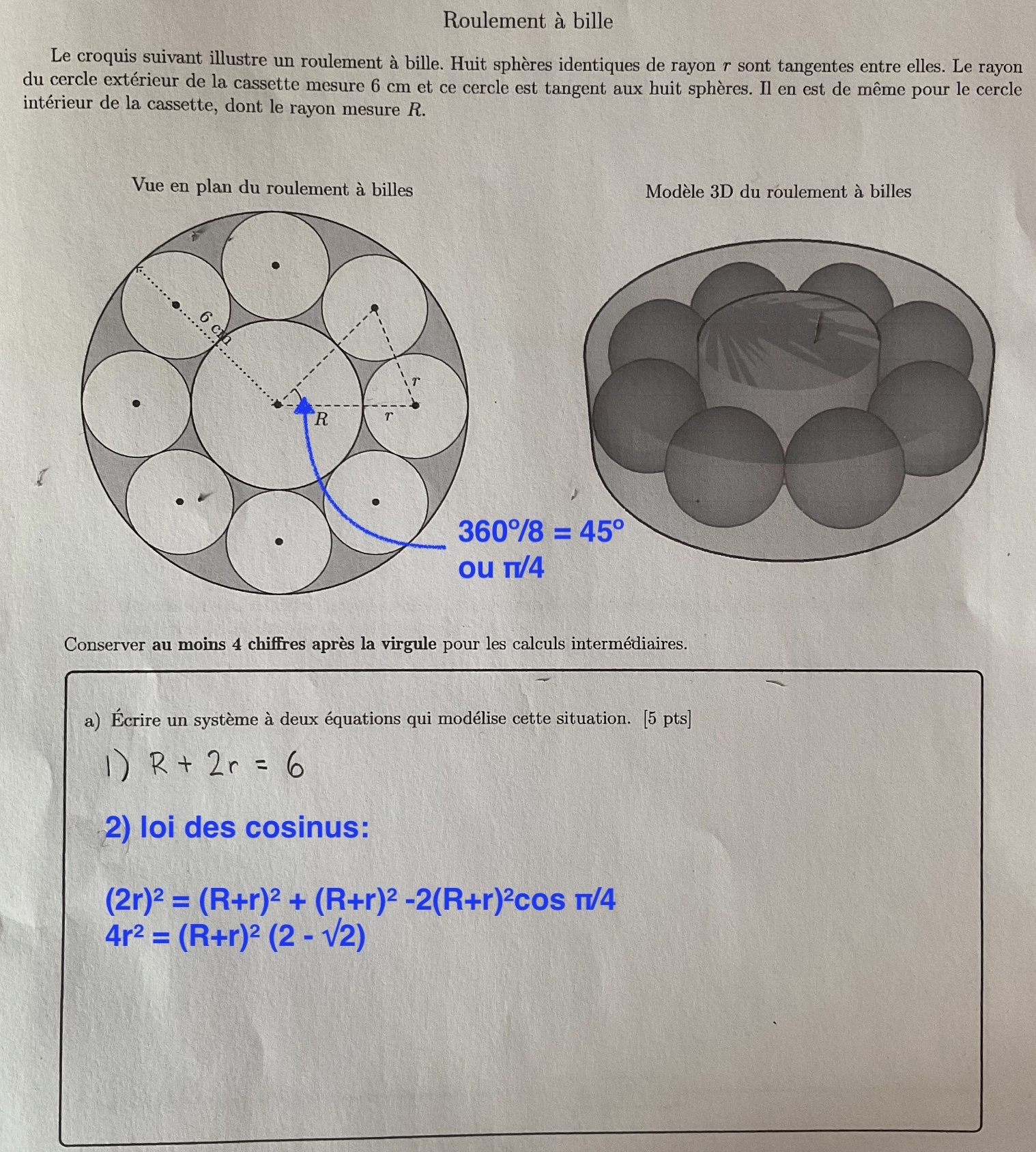
Pour trouver la valeur des variables r et R, tu dois résoudre le système d'équations que nous avons trouvé précédemment, soit :

$$ R+2r=6$$

$$4r^2=(R+r)^2(2-\sqrt{2})$$

Pour ce faire, utilisons la méthode de substitution. Nous allons commencer par isoler R dans la première équation :

$$ R+2r=6$$

$$ R+2r-2r=6-2r$$

$$ R=6-2r$$

Puis, nous allons insérer l'expression correspondante à la variable R dans la seconde équation, comme ceci :

$$4r^2=(R+r)^2(2-\sqrt{2})$$

$$4r^2=((6-2r)+r)^2(2-\sqrt{2})$$

On simplifie l'équation :

$$4r^2=(6-2r+r)^2(2-\sqrt{2})$$

$$4r^2=(6-r)^2(2-\sqrt{2})$$

$$4r^2=(6-r)^2(0,5858)$$

Nous allons maintenant développer l'expression, plus particulièrement le (6-r)² :

$$4r^2=(6-r)(6-r)(0,5858)$$

$$4r^2=(36-6r-6r+r^2)(0,5858)$$

$$4r^2=(36-12r+r^2)(0,5858)$$

$$4r^2=(36-12r+r^2)(0,5858)$$

On distribue la multiplication sur chaque terme de la parenthèse :

$$4r^2=21,088-7,029r+0,5858r^2$$

On déplace le terme du côté gauche de l'équation :

$$4r^2-4r^2=21,088-7,029r+0,5858r^2-4r^2$$

$$0=21,088-7,029r+(0,5858-4)r^2$$

$$0=21,088-7,029r-3,414r^2$$

On peut réordonner nos termes pour que l'expression soit plus lisible :

$$0=-3,414r^2-7,029r+21,088$$

Tu peux ensuite utiliser la formule quadratique pour résoudre cette équation.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

$$ x_{1,2} = \frac{-(-7,029) ± \sqrt{(-7,029)^2-4(-3,414)(21,088)}}{2(-3,414)} $$

Je te laisse faire le dernier calcul. Voici une fiche qui pourrait t'être utile : La résolution de systèmes d'équations linéaires | Secondaire | Alloprof

Si tu as d'autres questions, on est là! :)

Bonjour

J'aurais une question spécialement pour Katia K mais les autres vous pouvez répondre aussi!

Quand Katia K m'as répondue a cette question( voici le lien: https://www.alloprof.qc.ca/zonedentraide/discussion/55682/question/p1#Comment_73497) Je n'ai pas compris le mot «côtés».

Voici la vraie feuille: https://www.alloprof.qc.ca/zonedentraide/discussion/55682/question/p1#Comment_73497

Voici la feuille que je me questionne le mot «côtés»:

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

(Je suis sacrément désolé du barbouillage inapproprié)

Zhilan

@@

Tu as eu une réponse plus complète de Fer dans un message précédent.

.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.