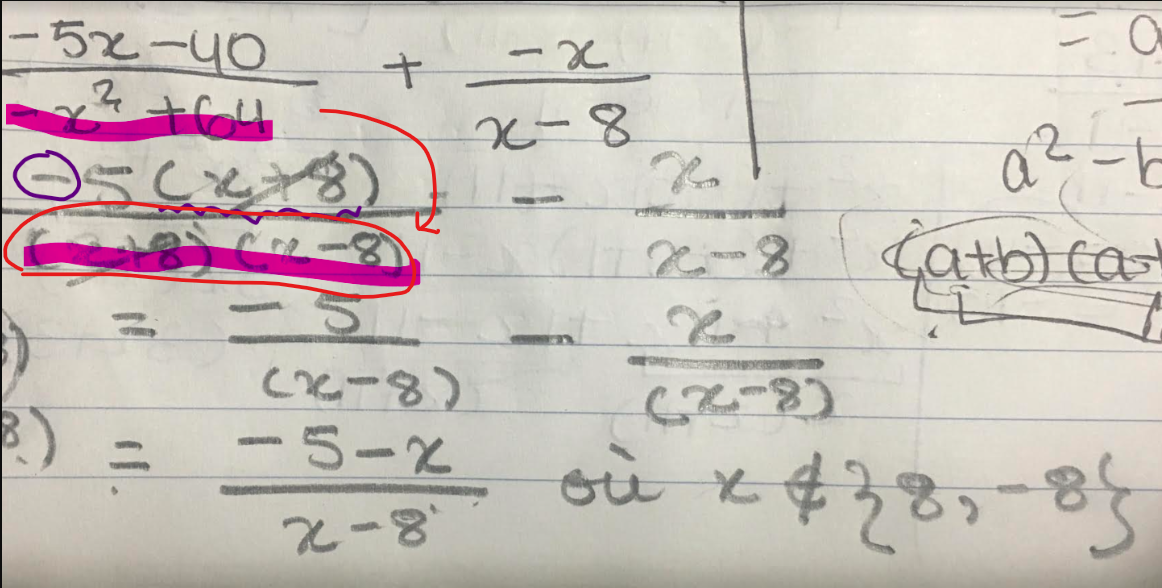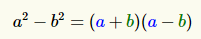Best Of

Salut!

Concernant ta première question, ton erreur est ici :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

En effectuant la différence de carrés de \(-x²+64\), on obtient ceci :

$$ -x^2+64$$

$$ 64-x^2$$

$$ 8^2-x^2$$

$$ 8^2-x^2$$

On applique ensuite l'identité :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce qui nous donne :

$$ 8^2-x^2$$

$$ (8+x)(8-x)$$

et non \((x+8)(x-8)\) !

Nous avons donc :

$$ \frac{-5(x+8)}{(8+x)(8-x)} - \frac{x}{x-8}$$

que l'on peut réécrire comme ceci :

$$ \frac{-5(x+8)}{(x+8)(-x+8)} - \frac{x}{x-8}$$

Tu peux ensuite éliminer le facteur commun \((x+8)\) :

$$ \frac{-5}{-x+8} - \frac{x}{x-8}$$

Pour mettre les deux termes sur un même dénominateur, tu dois factoriser un signe négatif dans le dénominateur de l'un des deux termes. Factorisons -1 dans le dénominateur du premier terme :

$$ \frac{-5}{-(x-8)} - \frac{x}{x-8}$$

Les deux signes négatifs s'annulent :

$$ \frac{5}{x-8} - \frac{x}{x-8}$$

Et on rassemble nos termes en un seul :

$$ \frac{5-x}{x-8}$$

Finalement, on peut réécrire l'expression comme ceci :

$$ \frac{-x+5}{x-8}$$

Voilà!

Dans la démarche du corrigé, on procède un peu différemment. Ils ont décidé de factoriser 5 au lieu de -5, puis de factoriser un signe négatif dans l'expression trouvée de la différence de carrés, ce qui donne :

$$ \frac{5(-x-8)}{(x+8)(-x+8)} - \frac{x}{x-8}$$

$$ \frac{5(-x-8)}{-(-x-8)(-x+8)} - \frac{x}{x-8}$$

Et on factorise encore un signe négatif, cette fois dans la seconde parenthèse :

$$ \frac{5(-x-8)}{-(-x-8)(-(x-8))} - \frac{x}{x-8}$$

Les deux signe négatifs s'annulent (-1 × -1 =1) :

$$ \frac{5(-x-8)}{(-x-8)(x-8)} - \frac{x}{x-8}$$

On peux alors annuler le terme commun \((-x-8)\) :

$$ \frac{5}{x-8} - \frac{x}{x-8}$$

Cette démarche nous permet d'avoir directement le même dénominateur que la seconde fraction.

Pour ton second exercice, ta démarche est bonne! ;) Dans une expression contenant des fractions rationnelles, tu dois te servir de tous les dénominateurs de ces fractions pour poser tes restrictions, et non un seul d'entre eux. De plus, lorsque tu divises des fractions rationnelles, puisque tu devras inverser le numérateur et le dénominateur, tu dois alors poser tes restrictions selon le numérateur et le dénominateur. Il est donc normal que tes restrictions soient selon (4x-9), (4x+9)(4x-9) et (3x-10)(3x-10).

Voici un exemple similaire issu de cette fiche : La division de fractions rationnelles | Secondaire | Alloprof

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

J'espère que c'est plus clair pour toi, sinon, n'hésite surtout pas à nous réécrire! :)

Coucou!

Bonjour

Dans ce cas-ci le but serait de faire les opérations sans déterminer ce que y veut dire, si cela aide voici la solution:

3(-4y+6)-8

=-12y+18-8 (on a distribué le 3 à la parenthèse)

=-12y+10 (on a rassemblé les termes semblables)

J'espère que ça répond à ta question! ;)