Secondary IV • 2yr.
Re-bonjour!
Dans une de mes questions précédantes, je n'ai pas eu la réponse complète de mes doutes. Mais, j'apprécie l'aide de l'enseignante qui m'ai aidé :) Pouvez-vous la compléter s.v.p?
1) Pour cette problème d'addition, voici comment j'ai effectué ma démarche.
Alors que la solution affiche ceci. Je ne comprends pas pourquoi cette différence de carrées n'est pas écrit comme (x+8) (x-8). J'ai mis en couleur les parties que j'ai fait autrement dans ma démarche. Aidez-moi à cibler mes erreurs s.v.p!
2) 1) Dans cette division, j'ai posé mes restrictions deux fois dans les morceaux en rose et mauve. Est-ce correct de les effectuer dans deux endroits?
Merci encore une fois de votre superrrrrrr aide :)
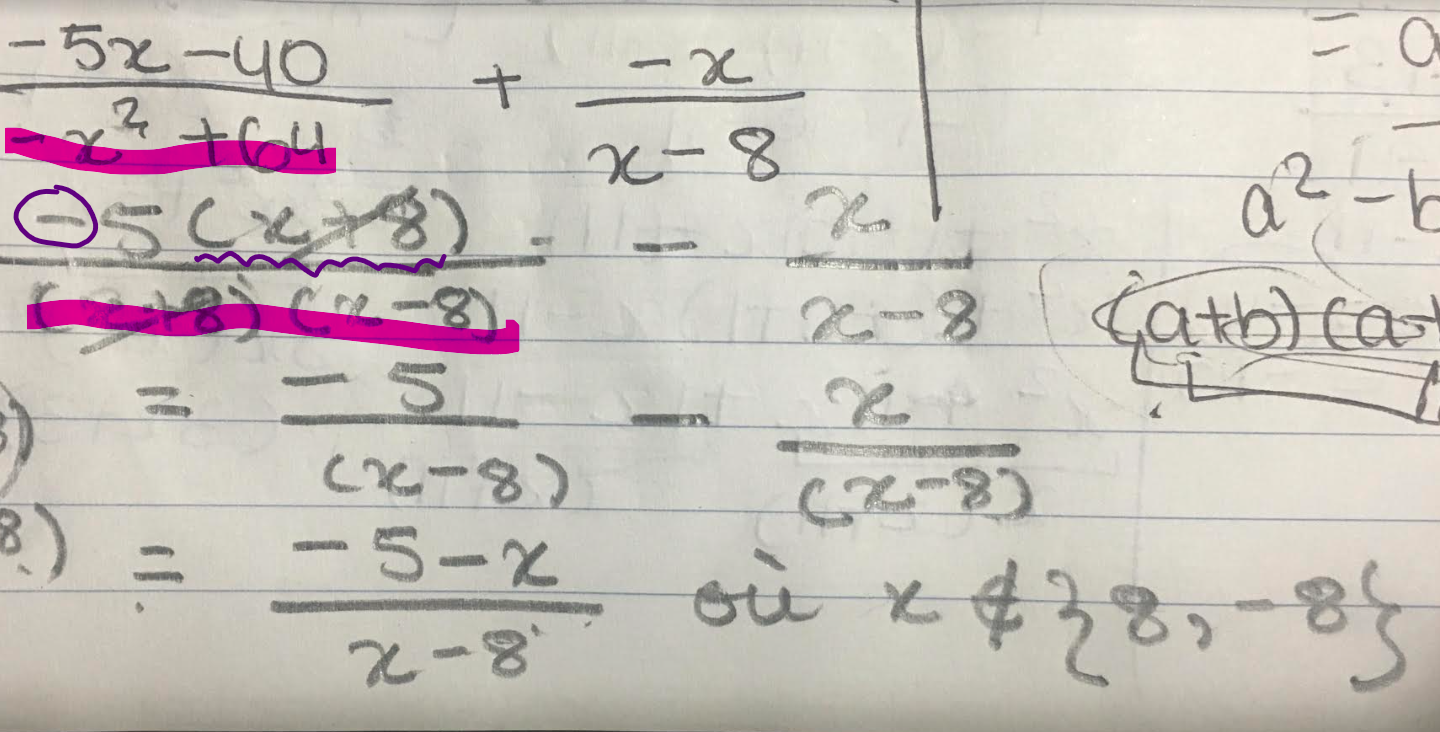

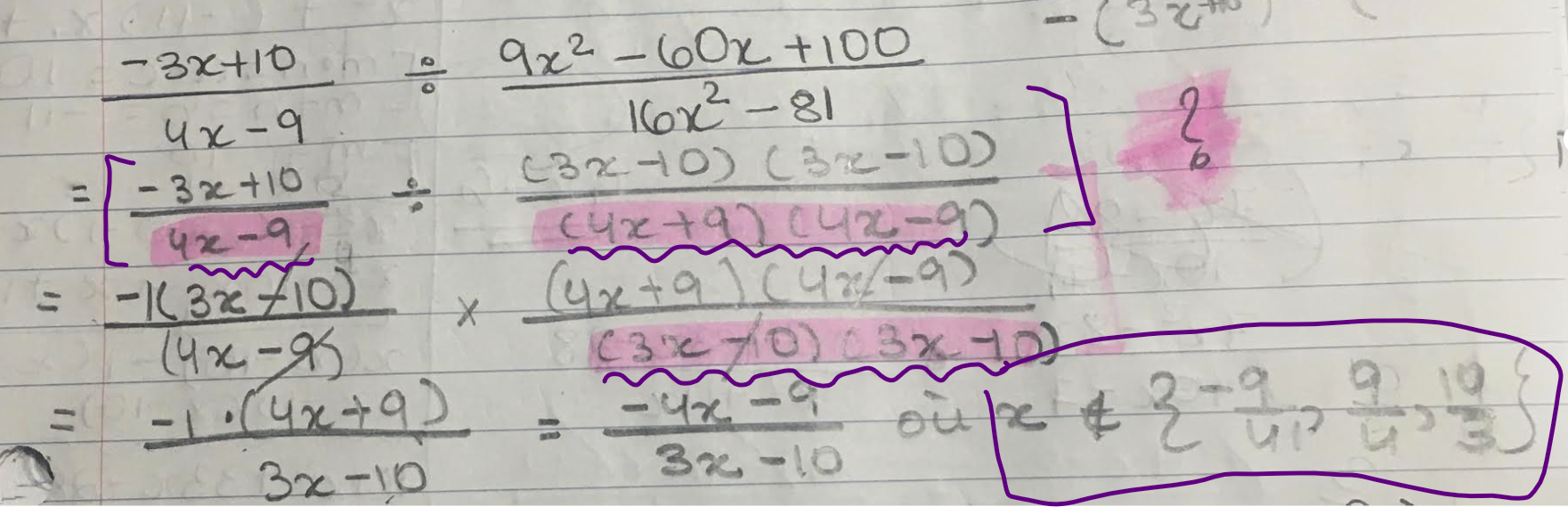






Salut!
Concernant ta première question, ton erreur est ici :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
En effectuant la différence de carrés de \(-x²+64\), on obtient ceci :
$$ -x^2+64$$
$$ 64-x^2$$
$$ 8^2-x^2$$
$$ 8^2-x^2$$
On applique ensuite l'identité :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce qui nous donne :
$$ 8^2-x^2$$
$$ (8+x)(8-x)$$
et non \((x+8)(x-8)\) !
Nous avons donc :
$$ \frac{-5(x+8)}{(8+x)(8-x)} - \frac{x}{x-8}$$
que l'on peut réécrire comme ceci :
$$ \frac{-5(x+8)}{(x+8)(-x+8)} - \frac{x}{x-8}$$
Tu peux ensuite éliminer le facteur commun \((x+8)\) :
$$ \frac{-5}{-x+8} - \frac{x}{x-8}$$
Pour mettre les deux termes sur un même dénominateur, tu dois factoriser un signe négatif dans le dénominateur de l'un des deux termes. Factorisons -1 dans le dénominateur du premier terme :
$$ \frac{-5}{-(x-8)} - \frac{x}{x-8}$$
Les deux signes négatifs s'annulent :
$$ \frac{5}{x-8} - \frac{x}{x-8}$$
Et on rassemble nos termes en un seul :
$$ \frac{5-x}{x-8}$$
Finalement, on peut réécrire l'expression comme ceci :
$$ \frac{-x+5}{x-8}$$
Voilà!
Dans la démarche du corrigé, on procède un peu différemment. Ils ont décidé de factoriser 5 au lieu de -5, puis de factoriser un signe négatif dans l'expression trouvée de la différence de carrés, ce qui donne :
$$ \frac{5(-x-8)}{(x+8)(-x+8)} - \frac{x}{x-8}$$
$$ \frac{5(-x-8)}{-(-x-8)(-x+8)} - \frac{x}{x-8}$$
Et on factorise encore un signe négatif, cette fois dans la seconde parenthèse :
$$ \frac{5(-x-8)}{-(-x-8)(-(x-8))} - \frac{x}{x-8}$$
Les deux signe négatifs s'annulent (-1 × -1 =1) :
$$ \frac{5(-x-8)}{(-x-8)(x-8)} - \frac{x}{x-8}$$
On peux alors annuler le terme commun \((-x-8)\) :
$$ \frac{5}{x-8} - \frac{x}{x-8}$$
Cette démarche nous permet d'avoir directement le même dénominateur que la seconde fraction.
Pour ton second exercice, ta démarche est bonne! ;) Dans une expression contenant des fractions rationnelles, tu dois te servir de tous les dénominateurs de ces fractions pour poser tes restrictions, et non un seul d'entre eux. De plus, lorsque tu divises des fractions rationnelles, puisque tu devras inverser le numérateur et le dénominateur, tu dois alors poser tes restrictions selon le numérateur et le dénominateur. Il est donc normal que tes restrictions soient selon (4x-9), (4x+9)(4x-9) et (3x-10)(3x-10).
Voici un exemple similaire issu de cette fiche : La division de fractions rationnelles | Secondaire | Alloprof
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
J'espère que c'est plus clair pour toi, sinon, n'hésite surtout pas à nous réécrire! :)
Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Bonjour,
Pour ta première question, tu as simplement mal factorisé. Voici comment faire :
-x^2 + 64 =
-(x^2 - 64) = différence de carrés
-(x^2 - 8^2) = -((x - 8)(x + 8)) = -(x - 8)(x + 8) =
(x - 8)* -(x + 8) = (x - 8)* (-x - 8)
Par la suite, 5 (-x-8) = -5(x+8), donc pas d'erreur de ce côté, mais pour enlevé facilement (-x - 8), on va préférer 5 (-x-8) au numérateur.
Pour ta deuxième question, cela est correct.
Bonne journée :)