Best Of
Question
Bonjour, pourriez-vous m'aider avec un travail, je ne comprends pas comment le faire. Je comprends ce qu'ils veulent, mais j'ignore le nombre de possibilités.
Merci beaucoup en avance pour la réponse :)
DiamantLogique5009
Question
Je ne comprend pas comment différencier une expression algébrique d'une égalité ou d'une équation. Pourriez-vous m'aider?
Question
Salut ! C'est quoi une constance et un coefficient avec definition et exemple svp ?
Question
Comment faire un exposant sur ordinateur et iPad pour completer ma réponse
Question
Bonjour à tous,
Pendant mon cours de Math mon prof a mis une énigme que je n'ai jamais résolu et qu'il n'ait jamais expliqué le raisonnement ou la raison. Voici l’énigme:
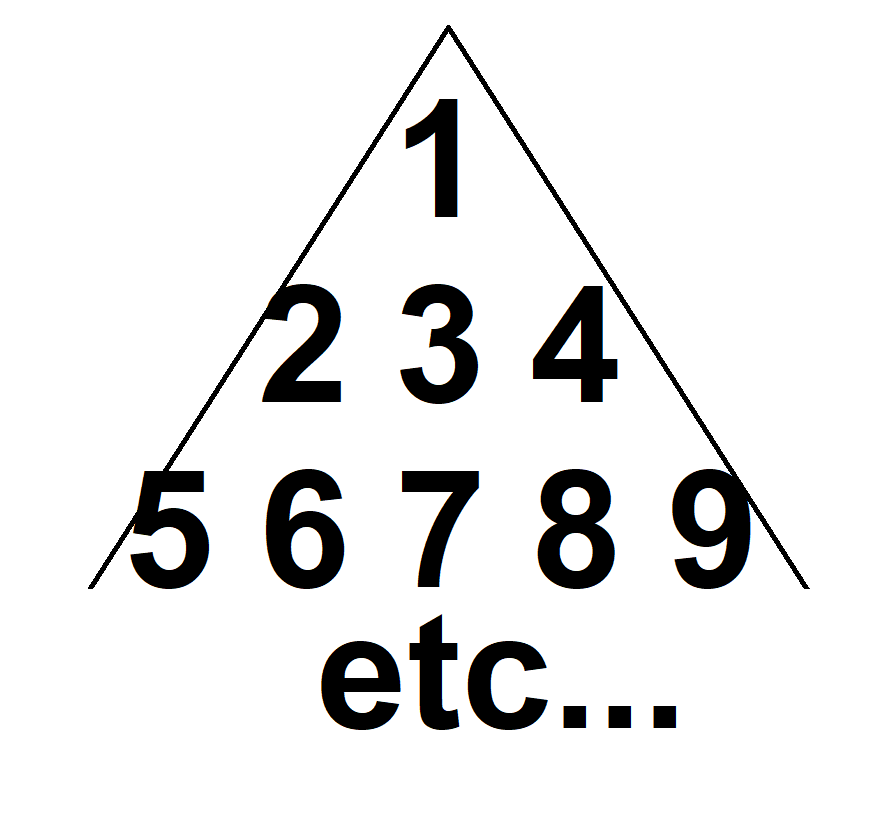
Rogadien demeure dans un immense bloc appartement égyptien. Ce grand immeuble a la forme d'une pyramide* et les appartements sont numérotés de la manière présenté dans l'image en pièce jointe.
La nuit dernière, sont voisin du dessus écoutait du Nickelback très fort et cela agaça profondemment Rogadien; Rogadien veut aller le voir, mais il ne sait pas le numéro de l'appartement de son voisin d'en haut immédiat.
Si Rogadien habite le 2019, quel est le numéro de l'appartement de son voisin du dessus?
Quelqu'un peut me dire comment résoudre ce problème? Merci beaucoup 😊!
Question
bonsoir est ce que je peux savoir comment résoudre l'équation suivante merci:
2x/x+4 + x/x^2-4