Best Of
Re: Question
Salut RubisSarcelle5226! 😎
Typiquement, les enseignants vont récupérer les feuilles de note pour les consulter au besoin (soupçons de triche par exemple). Ils vont ensuite les garder un certain temps avant de s'en débarrasser. Sans connaitre ton école en particulier, ce temps est typiquement assez long (jusqu'à la prochaine rentrée).
Donc, en contactant ton école/enseignant, il y a de fortes chances que celui-ci puisse te la remettre sans problème!
bon succès pour ta reprise! Ne te gêne pas si tu as d’autres questions, ça va me faire plaisir d’y répondre! 😊
PoutineOrange5768
Re: Question
Salut LoupJuste1279! 😎
Ce processus va être unique (les dates) à chaque centre de service.
Tout d'abord, ils doivent connaitre le nombre d'élève qui va y avoir dans chaque niveau, profil, sport étude etc. Ensuite, avec ces nombres, ils vont décider le nombre de classe par matière/niveau pour les assigner à un enseignant.
Une fois ces étapes complétées, les élèves vont être assignés à leur groupe.
Donc, selon ton centre de service, ce processus pourrait déjà être complété, ou bien il va l'être rendu plus proche de la rentrée.
Ne te gêne pas si tu as d’autres questions, ça va me faire plaisir d’y répondre! 😊
PoutineOrange5768
Re: Question
Tu veut dire le ou la souris ou rat qui est une BD qui éxiste?
J'pourrais te dire une solution pour régler le problème si tu veut.Si tu veut que ton mot de passe,ton Pseudo que je n' comprend pas et ton souvenir de toi.Si tu ne peut pas,tu va créer ton profil.(un prfil est un compte que tu utilise pour que la prochaine fois que tu te connecte,tu n'aurras plus de problème de te connecter.Mais attention!Ils te donneront un temps de combien de jours,de mois et années de ton abonnement ou connexion.Donc tu ne va pas rester connecté toute ta vie.Tu devras donc te connecter chaque fois lorsque tu te deconnecteras.
Re: Question
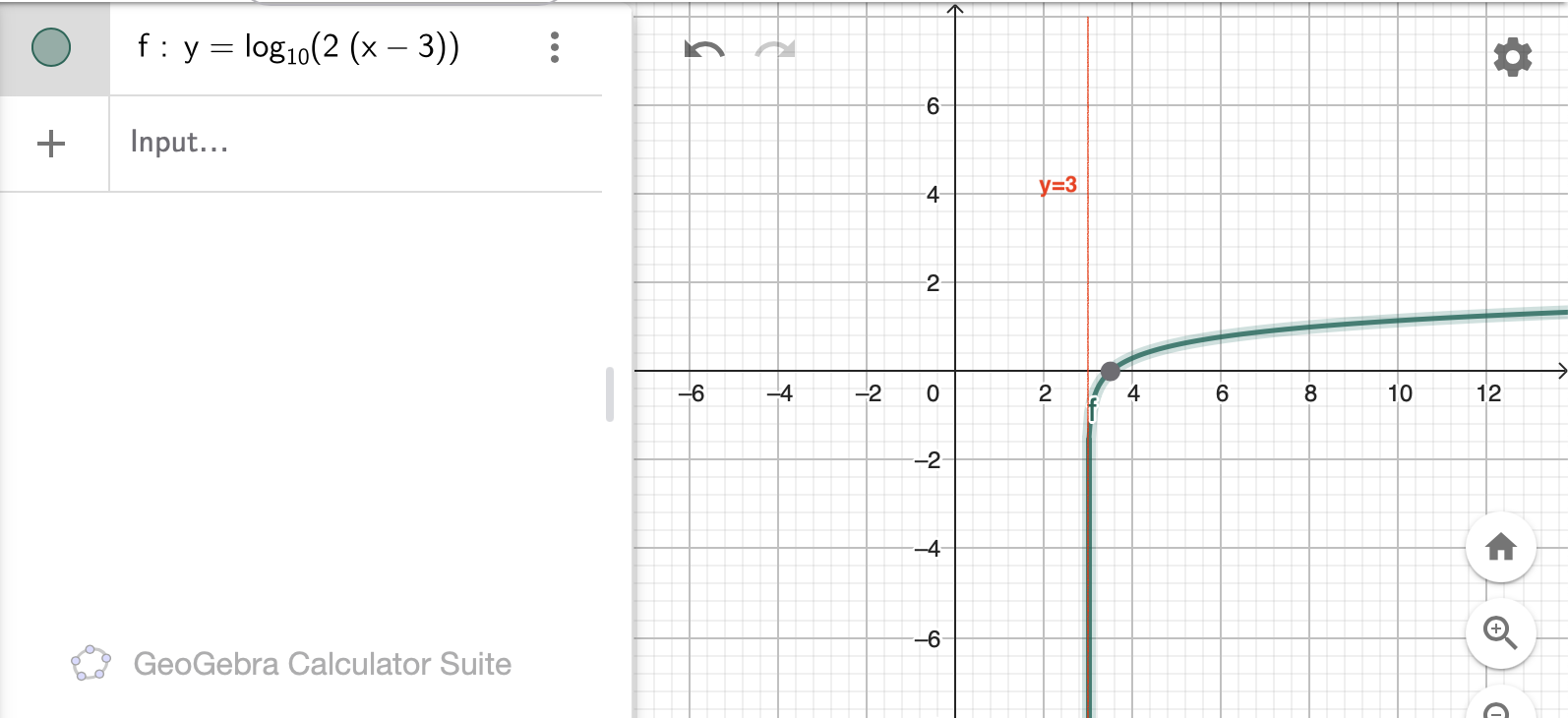
The asymptote of a function is a value that the function approaches but never reaches.
In this case it is y = h
In the following example with a = 1, b = 2, c = 10 and h = 3, the asymptote is y = 3 and the zero of the function is 3.5. (The lines are very close but they never meet even though it is hard to see because of a lack of precision: it is hard to draw lines that are infinitely thin...)
Re: Question
Bonjour, merci beaucoup pour ta question ! 😄
Je te partage cette fiche sur la lettre ouverte, dans laquelle tu trouveras plusieurs informations pertinentes (structure de la lettre ouverte, exemples de lettre ouverte et plus encore) : https://www.alloprof.qc.ca/fr/eleves/bv/francais/la-lettre-ouverte-f1117 🙂
Question
Allô Prof, est-ce que je peux mettre dans mon sujet amené une statistique ou une information qui ne se trouve pas dans les textes documentaires envoyés par le Ministère, mais que j’ai trouvée dans un autre article que j’ai lu?
De plus, si je peux le faire, est-ce que je dois l’écrire dans ma feuille de notes avec les sources? (Examen ministerial français 5)
Merci!
Re: Question
C'est beaucoup d'essai-erreur, mais avec la pratique ça devient plus facile.
En 1) par exemple, comme tu dois réduire l'expression et que tu as (x-1) au dénominateur, tu vas chercher à savoir quel binôme (ax+b) multiplié à (x-1) donnerait x² + 5x -6.
Tu sais déjà que le a = 1 puisque tu as 1x².
(x - 1)(x + b) = x² + 5x -6
Pour le second terme, b, il faut que
(-1) + b = 5 (la constante du terme en x) et que
(1) · b = -6 (le terme constant de la fin de x² + 5x -6)
=> b = -6
En 2) avec x² + 5x - 14, note que 2 · 7 = 14 et 7 - 2 = 5 et tu peux déduire tes deux facteurs.
Pour 3x² + 23x + 14 tu sais déjà que tu auras un terme (3x + ?) et un autre (x + ?). Note aussi que 2 · 7 = 14, 3 · 7 = 21 et 21 + 2 = 23.
Je te laisse faire tes essais.
Les restrictions pour les dénominateurs sont que les facteurs trouvés pour l'expression avant sa réduction, doivent être différents de 0.
En 1) cela signifie que (x - 1) ≠ 0 => x ≠ 1
Re: Question
Mais ce n'est pas toujours le cas. Tu as un contexte pour cette question?
L'abscisse à l'origine par définition est la valeur de x quand y = 0.
Si l'abscisse à l'origine est de 0 cela veut dire que la fonction quadratique en question passe par (0,0).
Re: Question
Bonjour,
Merci pour ta question!
Pour compléter la réponse de FerUpsilon5520, je te conseille d'aller consulter la fiche explicative suivante sur les propriétés de la fonction quadratique :
N'hésite pas à préciser ta question ou pour tout autre questionnement!
Zachary T. :)