Best Of
Re: Question
Salut !
L'expression de cette idée remonte il y a de cela très longtemps. Ainsi, il n'y a pas une seule personne à qui l'on puisse attribuer la découverte de cette réalité.
Par exemple, il existe plusieurs philosophes et mathématiciens grecques (Pythagore, Platon, Aristote, etc.) qui ont contribué à l'émergence de cette théorie qui a pu être prouvée par la suite.
Si tu as d'autres questions, n'hésite pas !
Re: Question
Salut !
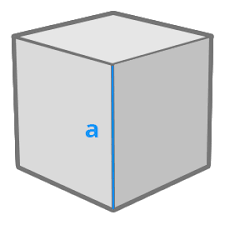
Comme le but est de déterminer les mesures d'une boîte pour entreposer les savons, il te faut connaître le volume de chaque savon dans un premier temps.
En connaissant leur masse et leur densité, tu peux en calculer le volume. Tu dois diviser la masse par la densité. Avec ce volume, tu peux trouver la valeur de la mesure a de côté.
Tu dois tenir compte des incertitudes.
Par la suite, tu dois déterminer les mesures d'une boîte qui va contenir les savons et déterminer le nombre de feuilles que le menuisier doit utiliser. Je te laisse essayer par toi-même et si tu as d'autres questions, n'hésite pas !
Re: Question
Salut,
C'est bien parti. Je comprends que le carré a une aire de 8 cm², mais on ne dit pas que la mesure de son côté est \(x\). La mesure du côté du carré est bien \(\sqrt{8} = 2\sqrt{2}\) cm, mais ce n'est pas égal à la mesure de \(x\). De toute façon, on n'a pas besoin de la mesure du côté du carré, on a juste besoin de son aire pour poser l'équation.
Pour l'aire du trapèze, j'obtiens aussi \(16x^{2}-10x\) cm².
Pour l'aire de l'autre figure, tu peux additionner l'aire du rectangle « vertical » de \(12\) par \(x\), soit \(12x\), à celui du rectangle « horizontal » de \(8\) par \(x\), soit \(8x\). Tu obtiens \(12x + 8x = 20x\) cm². Cependant, en faisant ça, on compte le carré de \(x\) par \(x\) en double. Il suffit de soustraire une fois \(x^{2}\). L'aire de la figure en « L » est donc \(20x - x^{2}\) cm².
L'aire des deux figures ensemble est donc :\[20x -x^{2}+8\]
Il faut résoudre \begin{align*}16x^{2}-10x&= 20x+8 \\ \\ 17x^{2}-30x-8&=0\end{align*}
Tu peux essayer la méthode somme-produit, la complétion du carré ou la formule quadratique. Il y a deux solutions rationnelles, une positive et une négative, mais comme \(x>0\) car \(x\) est la mesure d'un côté de la figure en « L », tu n'en garderas qu'une seule.
À toi de jouer !
Re: Question
Salut :D
Interagir en chimie signifie faire une réaction chimique.
J'espère que ça t'aide. :)
Dis-nous si tu ne comprends toujours pas.
Re: Question
Salut :D
Je te suggère de consulter un moteur de recherche universitaire, qui regroupe plusieurs études sur le sujet. Quelques unes sont en anglais, mais c'est un sujet assez précis, alors il est possible que les résultats scientifiques soient seulement disponibles dans cette langue.
Je te le mets ici. :)
Bonne recherche :D N'hésite pas si tu as d'autres questions :)
Re: Question
@ argent
On transforme la soustraction en une addition de l'opposé:
exemples :
a) 65 - -17 = 65 + +17 = 65+17
b) -24 - 18 = -24 + -18
c) 8 - 22 = 8 + -22
Question
Bonjour, :) j’ai une question : Est ce que il y a des applications pour étudier avant le jour des examens ? Merci d’avance !
Re: Question
Allo HibouAgile8884,
Merci pour ta question!
Tu devrais les inverser car le a^3 à priorité sur le a^2.
J'espère t'avoir aidé!
Lea-Kim