Best Of
Re: Question
Salut à toi !
Merci pour ta question. :)
Dans cet exercice, on te demande de reformuler la phrase proposée en une phrase interrogative. Ainsi, tu dois accorder adéquatement le verbe "to grow" en plus d'utiliser la bonne formulation de phrase !
Pour t'aider, je t'invite à consulter cette fiche qui porte sur le sujet !
N'hésite pas si tu as d'autres questions !
Océane :)
Re: Question
Bonjour!
Un précipice, c'est un gouffre très profond. Lorsqu'on se trouve devant un précipice, on se retrouve devant quelque chose de très creux. Ça peut être un trou, une falaise, etc.
J'espère t'avoir aidé! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Bonjour!
Non, cela n'est pas obligatoire. Tu peux en mettre un s'il s'agit de l'intonation que tu veux donner à ta phrase. :)
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Bonjour!
Nous avons justement une fiche sur ces homophones! La fiche explique bien la différence entre chacun, je te suggère de la lire! :D
La voici
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Salut!
C'est faux. La somme de deux nombres rationels donne toujours un nombre rationel. C'est leur propriété!
J'éspère que ça t'aide:)
Re: Question
Salut :D
La somme des carrés se représente comme ça :
$$3^2 + (-4)^2$$
Bonne résolution :D
N'hésite pas à nous montrer comment ça avance. :)
Re: Question
Salut :D
Je te suggère ces quelques fiches afin de réviser. :)
N'hésite pas si tu as des questions en cours de révision :D
Re: Question
- Ça ce n'est pas bien.
- Ce n'est pas bien.
- Cela peut nuire au développement de la société.
- Celui de mon ami me plait.
- Aucun n'est mieux.
- Certains sont grands, d'autres sont petits.
- Chacun doit prendre sa trousse.
- Personne ne connait la réponse.
Pour le reste je ne sais pas trop, j'espère que cela t'aidera.
Re: Question
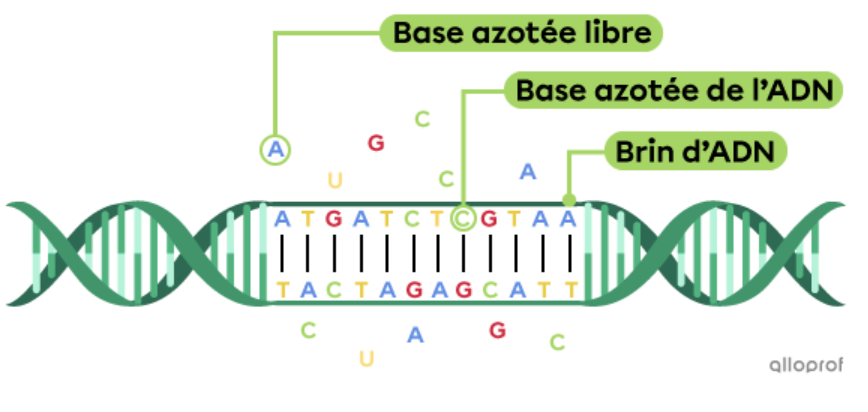
Bonjour HibouSage,
Merci pour ta question!
Pour la question a), souviens-toi que l'ADN est composé de deux brins, et que chaque base azotée présente sur un brin est associé à une autre base azotée sur le deuxième brin. Les associations des bases se font ainsi:
Chaque base de cytosine est donc associée à une base de guanine dans l'ADN.
Pour la question b), il faut savoir qu'il existe seulement quatre bases azotées possibles dans l'ADN. La guanine et la cytosine s'associent et sont donc présentes en même quantité (24% et 24% pour un total de 48%). Les 52% restants sont partagés également entre la thymine et l'adénine, qui s'associent aussi. Il y a donc 26% d'adénine dans le gène.
Tu peux consulter cette fiche au besoin:
N'hésite pas si tu as encore besoin d'aide:)
Kylan
Re: Question
Bonsoir,
Un pronom indéfini est un pronom qui est général, qui n'indique pas quelque chose ou quelqu'un en particulier.
Exemple : chacun, quelque chose, quelqu'un, aucun.
Voici une fiche sur le sujet :
Bonne soirée,
Audrey