Best Of

0,15km = 150m

donc 1km= 1000m

Tout est bon. Voici mes commentaires

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

En a) le domaine est l'ensemble des valeurs que x pent prendre; la courbe est aussi longue que l'axe des x, c'est pourquoi le domaine est l'ensemble des réels, c'est-à-dire toutes les valeurs possibles sur l'axe.

Le co-domaine est aussi l'ensemble des valeurs que peut prendre y. Il s'agit de l'ensemble des réels parce que les pentes ne sont pas nulles, la courbe continue de descendre ou de monter même si la progression est lente (en particulier à droite).

La variation (la pente) est positive (au sens large ce qui inclus une variation nulle) sur -∞, 1] (on peut mettre ]-∞,1] aussi mais jamais [-∞,1] car l'infini n'est pas borné); ensuite elle est négative (au sens large ce qui inclus une variation nulle) sur [-2,3] puis elle est positive sur [3,+∞

Salut!

L'algèbre est une branche des mathématiques qui utilise des lettres et des symboles pour représenter des nombres et exprimer des relations entre eux. Elle permet de résoudre des équations et de manipuler des expressions mathématiques de manière générale. Voici un exemple :

Imaginons que nous avons une boîte de bonbons. Nous ne savons pas combien il y a de bonbons dans cette boîte, alors nous dirons qu'il y a "x" bonbons. Si chaque bonbon coûte 2$, et qu'au total, nous payons 10$, alors nous avons l'équation :

$$ 2 \times x=10 $$

Cela signifie que le coût total des bonbons (2x) est égal à 10$. Maintenant, pour trouver combien de bonbons il y a dans la boîte, nous devons trouver la valeur de la lettre x. Pour ce faire, il faut résoudre cette équation algébrique. On trouvera alors que x=5, ce qui signifie qu'il y a 5 bonbons dans la boîte.

Tu étudieras cette notion plus en profondeur au cours de ton secondaire. Si tu es tout de même curieux/curieuse d'en apprendre davantage à ce sujet, tu peux consulter la section "algèbre" de cette fiche : Aide-mémoire – Mathématiques – Secondaire 1 et 2 | Secondaire | Alloprof

Bonne journée! :)

bonsoir est ce que je peux avoir des explications sur l algèbre svp??

Salut!

Je crois que le graphique est mal gradué (le point F nous indique que les graduations sont de 0,5 en x, mais cela ne concorde pas avec les coordonnées des autres points). Cela dit, de toute façon, tu n'as pas besoin de te fier à ces graduations, tu peux imaginer qu'elles ne sont pas là et résoudre le problème sans elles.

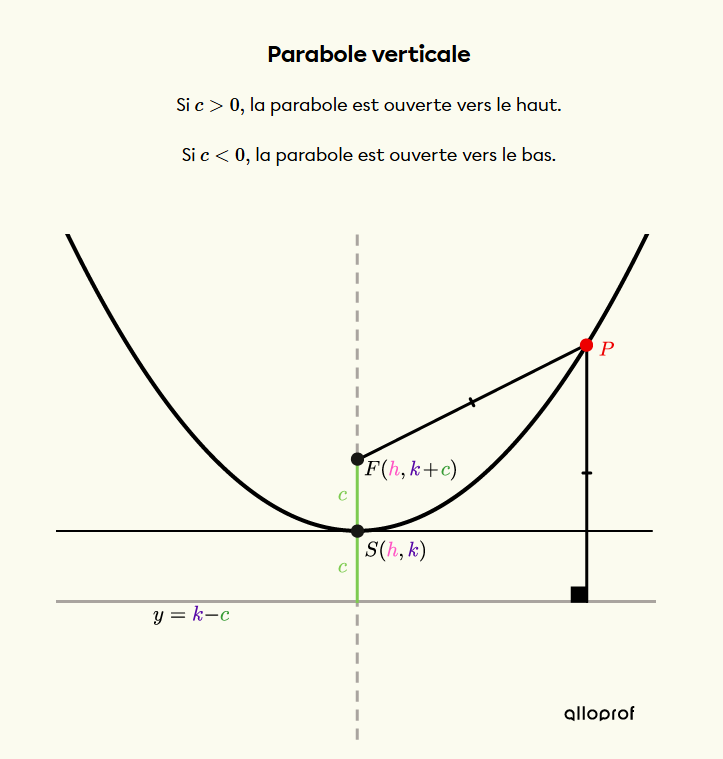
Pour trouver la règle de la parabole verte, tu peux utiliser le foyer ainsi que la coordonnée en x du sommet. On sait que h=0,5 :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce qui nous donne l'équation :

$$(x-h)^2=4c(y-k)$$

$$(x-0,5)^2=4c(y-k)$$

On connait aussi les coordonnées du foyer F, ce qui nous permet de poser cette équation :

$$F_{y}=k+c$$

$$-2=k+c$$

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

De plus, on sait que cette parabole passe par (3, 4). En insérant ces coordonnées dans notre équation, on obtient :

$$(3-0,5)^2=4c(4-k)$$

On a ainsi 2 équations et 2 inconnus!

$$-2=k+c$$

$$(3-0,5)^2=4c(4-k)$$

Puisqu'on a autant d'inconnus que d'équations, on peut résoudre un système d'équations afin de trouver la valeur des variables c et k.

Voici des fiches sur ces notions qui pourraient t'être utiles : 

• La résolution de systèmes d'équations linéaires | Secondaire | Alloprof
• La parabole (conique) | Secondaire | Alloprof

Je te laisse terminer. J'espère que c'est plus clair pour toi! :)

J'arrive au même résultat

parabole initiale de sommet (20,0) :

y = -5x²/36 + 20

parabole de sommet (30,0), seule la hauteur diffère:

y = -5x²/36 + 30

quand y = 0 => x = 6√6 = 2√54