Best Of
Re: Question
Salut à toi intrépide prodige! 😁
Ça nous fait plaisir que tu utilises Alloprof!
Oui!
Voici les éléments importants à inclure dans la conclusion.
Si tu souhaites réviser la structure du texte d'opinion, c'est par ici.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Bonjour!
Nous avons justement plusieurs fiches qui donnent des trucs pour étudier et réviser. En voici deux :
Trucs pour mieux étudier
Étudier plus efficacement : des techniques amusantes pour réussir ton prochain examen!
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Bonjour AdmirableStork6905,
Merci pour ta question!
On attribue au sieur de Laviolette la fondation de Trois-Rivières en 1634 avec l'établissement d'un fort permanent au croisement de la rivière Saint-Maurice et du fleuve Saint-Laurent. C'est Samuel de Champlain qui a désigné Laviolette, alors un employé de la traite des fourrures, pour commander ce poste de traite.
Je t'invite à consulter la fiche du Dictionnaire biographique du Canada sur Laviolette pour en apprendre davantage sur cet homme : http://www.biographi.ca/fr/bio/laviolette_m_1F.html
Je t'invite à consulter notre fiche sur les débuts de la colonisation en Nouvelle-France pour en apprendre plus sur cette époque : https://www.alloprof.qc.ca/fr/eleves/bv/histoire/les-debuts-de-la-nouvelle-france-h1515
N'hésite pas à nous réécrire si tu as d'autres questions!
Noémie
Re: Question
Hi HonourableDragon6239,
Thank you for your question! :)
The challenge with this exercise is that we need to find the right coordinates to help us determine the equations of the functions in this situation.
To begin, you’ll need to find the equation of the parabola. Based on the diagram and the symmetry, we can deduce that the zeros are located 120 cm from the center, and the vertex has coordinates (0, -60). With that information, you’ll be able to write the equation of the parabola, which will be useful later on :)
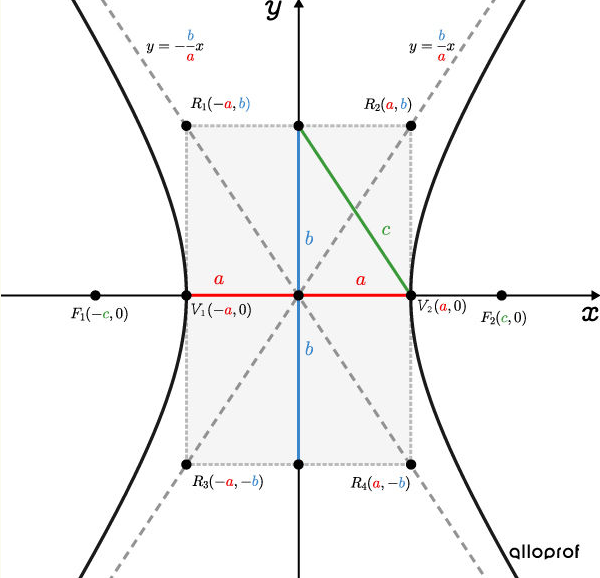
Next, we need to find the equation of the hyperbola. This part is a bit trickier, since we don’t know the coordinates of the vertex. However, from the diagram, we can see that the hyperbola passes through the point (-40, -120). Also, based on the information in the problem, we can deduce that the distance from the center to each focus is 100 cm. You can then use the Pythagorean theorem to have a first equation as shown in this image:
With c=100, you can have c^2=a^2 +b^2 as your first equation, and x^2/a^2 - y^2/b^2 = 1 as your second equation by substituting the point (-40, -120) for x and y. That system will allow you to find the values of a and b. Here is a link that could help you to find the equation: https://www.alloprof.qc.ca/en/students/vl/mathematics/hyperbola-conic-m1329
Once you have the equation of the hyperbola, the last step is to find the points of intersection between the geometric figures (the parabola and the rectangle), in order to determine the coordinates of points A, B, C, and D :)
Don’t hesitate to reach out if you have more questions!
Sandrine
Re: Question
Bonjour!
Une critique est toujours composée de deux parties : la partie informative et la partie appréciative.
La partie informative doit absolument être objective. Elle ne contient pas d'opinion.
La partie appréciative défend une opinion. Cependant, cela ne veut pas dire que la présence du « je » est obligatoire. Il ne faut pas oublier qu'il faut justifier à l'aide de critères d'appréciations et d'exemples.
Je te suggère de consulter la fiche ci-dessous pour en apprendre plus sur la critique littéraire :
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Bonjour FraiseAdorable5247,
Super question 👌
La force normale est la force exercée sur un objet par une surface en contact avec celui-ci, et elle doit toujours être perpendiculaire à la surface. Dans l'espace, si un élément n'est pas en contact avec une surface, il n'y a pas de force normale. À l'inverse, si un objet appuie contre une surface (par exemple, un astronaute qui pousse contre un mur dans la station), alors il y a une force normale :)
Par ailleurs, il y a encore de la gravité dans l’espace! En orbite terrestre, la gravité est juste un peu plus faible, mais elle existe toujours. Ce n’est donc pas l’absence de gravité qui fait disparaître la force normale, c’est l’absence de contact avec une surface.
N'hésite pas si tu as d'autres questions :)
Sandrine
Re: Question
Bonjour!
Je te suggère de regarder la vidéo ci-dessous, elle explique bien les explorations qui ont mené les européens en Amérique :
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Salut à toi intrépide prodige! 😁
Ça nous fait plaisir que tu utilises Alloprof!
C'est exactement ça! Et, techniquement, les particules qui nous composent (masse) ne change pas. On reste toujours soi-même!
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Bonjour,
Merci d'utiliser la zone d'entraide.
Malheureusement, pour la formation générale des jeunes, je n'ai pas trouvé d'école en ligne au Québec. Il est possible de faire l'école à la maison et d'avoir du soutien en ligne par des organisations privées, mais des structures d'écoles, je ne crois pas que c'est possible.
Pour en savoir davantage, tu peux consulter le centre de services scolaires de ta région, ils pourront certainement te donner l'information.
À bientôt,
Karen
Re: Question
Bonjour FraiseAdorable5247,
Merci beaucoup pour ta question! Je n’irai pas jusqu’à dire que la voiture est au repos. En effet, lorsqu’une voiture dérape, elle effectue un mouvement. Je dirai donc que le dérapage change l’accélération et que celle-ci devient négative, puisqu’une voiture ralentit lorsqu’elle dérape. Bref, je ne pense pas qu’il est vrai de dire que la voiture est au repos lorsque les roues se bloquent. Voici une fiche qui pourrait peut-être t’aider :
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!