Best Of
Re: Question
Salut à toi brave élève!
Ça nous fait plaisir que tu utilises Alloprof!
Un composé binaire est une substance qui comprend deux types d’atomes.
Le composé HCl est un composé binaire, puisqu’il comprend deux types d’atomes : H (hydrogène) et Cl (chlore).
Ces notions sont plutôt vues au secondaire.
As-tu un exemple d'exercice que tu souhaites voir ensemble?
Passe une belle journée :) Écris-nous si tu as d'autres questions!
Re: Question
Salut!
On est un peu en avance (ou en retard), mais merci quand même! 😄 Toute l’équipe d’Alloprof te souhaite plein de succès dans tes études :)
Re: Question
Bonjour,
Comme Alloprof n'est pas un service de correction, nous ne pouvons pas indiquer si ton résumé est bon ou non. Cependant, je peux te suggérer d'utiliser notre répertoire de révision pour t'aider à vérifier le contenu de ton résumé. Le voici :
Aussi, si tu as une question sur un élément ou une notion, n'hésite pas à nous réécrire. Nous serons heureux de t'aider!
Laurie :D
Re: Question
Bonjour DiamantMagnifique7187,
Merci pour ta question :)
Pour t'aider à monter une charge lourde sur une pente, tu peux utiliser des machines simples qui permettront de réduire l'effort à fournir. Tu peux par exemple utiliser une poulie et des cordes ou encore un plan incliné qui possède un angle plus petit que la pente.
Pour en apprendre davantage sur les machines simples, je t'invite à consulter le lien suivant: https://www.alloprof.qc.ca/fr/eleves/bv/sciences/les-types-de-machines-simples-s1427
N'hésite pas si tu as d'autres questions :)
Sandrine
Re: Question
Salut ! Je t'explique. Exemple j'ai trois (3) lapin et mon ami m'en donne 3 autre je fais donc 3 + 3 et sa donne 6 car je rajoute 3 lapin a ma ferme !) J'espère que sa ta aider !
Re: Question
Bonjour!
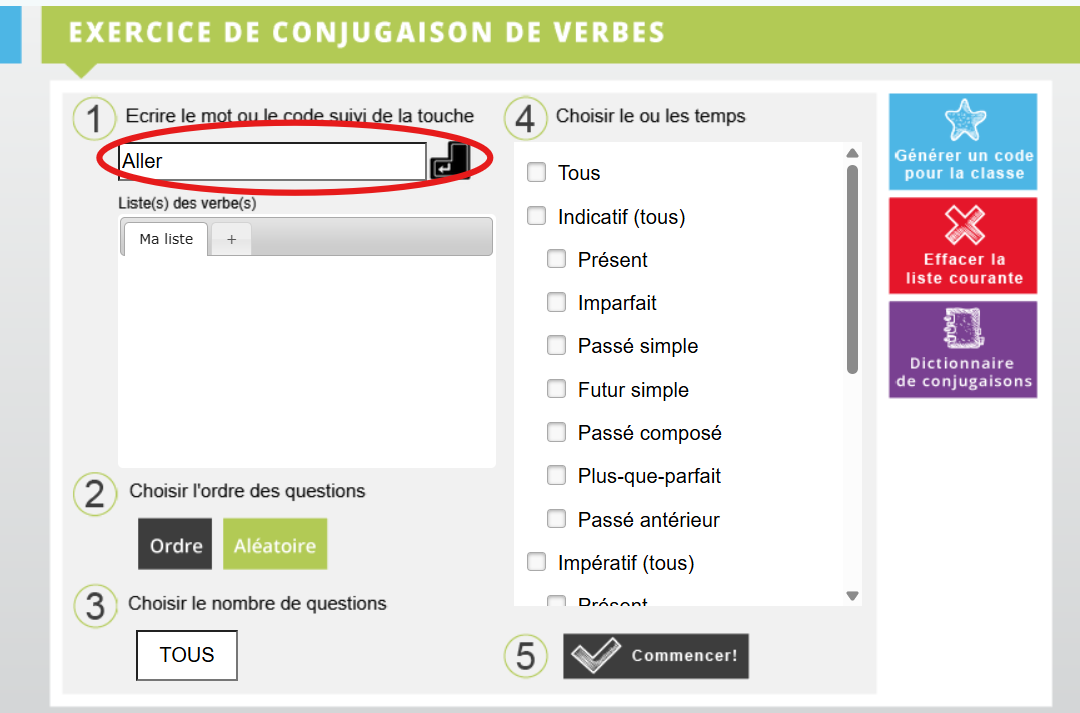
Pour commencer tu dois ajouter les verbes que tu veux réviser dans la barre prévue :
Clique sur le verbe, il s'ajoutera dans la section « Ma liste » juste dessous. Tu pourras ensuite choisir l'ordre des questions, le nombre de questions et le ou les temps de verbe que tu veux pratiquer.
Si tu veux créer un code pour partager ta liste, clique sur le carré bleu à droite, celui où on peut lire « Générer un code pour la classe ». La prochaine fois, à la place d'entrer les verbes pour créer une nouvelle liste, tu pourras entrer le code dans la barre et retrouver immédiatement ta liste! :D
J'espère t'avoir aidé! Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Cela dépend de l'examen dans laquel tu pourras utiliser la fiche aide mémoire. Par exemple, il serait bénéfique d'écrire des formules, des noms et même des rappels (si tu as fait des erreurs pendant la révision, pour ne pas en refaire pendant l'examen!)
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
En fait, si tu utilises la question "de quoi", il s'agit d'un complément indirect puisque tu utilises une préposition (de).
Par exemple,
Les clients comparent plusieurs modèles.
Les clients comparent quoi? Plusieurs modèles.
Il s'agit donc d'un complément direct.
Ils parlent de ses vacances.
Ils parlent de quoi? De ses vacances.
Il s'agit d'un complément indirect.
Mais pour t'aider à mieux identifier un CD et un CI, je te propose de connaitre d'autres manipulations syntaxiques. Ça t'aidera à valider ta réponse lorsque tu n'es pas certain.
Voici deux fiches pour t'aider:
N'hésite pas à revenir nous voir si tu as d'autres questions.
Karen
Re: Question
Bonsoir PerleTurquoise5427!
Pour le neuronne, il faut voir sa définition avant tout:
"Le neurone, ou cellule nerveuse, est la plus petite partie vivante du système nerveux responsable de la transmission de l'influx nerveux."
Qu'est-ce que l'influx nerveux alors?
"L'influx nerveux est une activité électrique qui se propage dans le système nerveux grâce à la stimulation de neurones successifs."
Pour ce qui est de sa composition, elle se définit de 3 parties:
Si tu veux connaître plus de détails, je t'invite à lire notre fiche sur le sujet via ce lien:
J'espère que ces informations répondent à ta questions!
N'hésite pas à communiquer avec nous si tu as d'autres questions!
ThonLucide8631