Best Of
Re: Question
Bonjour QuartzRose,
Merci pour ta question!
Je ne suis pas certain de comprendre? Tu veux savoir quel type de jeu impliquant des notions de probabilités serait le plus pertinent dans le cadre d'une kermesse pour prévenir la dépendance? Tu parles par exemple de jeux de type lancer de dés ou pile ou face?
Peux-tu me reconfirmer ce que tu veux dire en republiant sur la Zone? Il sera alors plus facile pour moi de t'aider:)
Kylan
Re: Question
Salut!
Regardons tout cela de plus près :D
Concernant ta première question, tu as tout à fait raison, si la force de la poussée est de la même norme que la force de frottement, alors les deux vecteurs s'annuleront.
Cependant, une somme des forces nulle ne veut pas dire que l’objet est immobile, ça veut dire qu’il n’accélère pas, donc la vitesse est constante, c'est pourquoi on a un MRU et non un MRUA.
Reprenons l'équation de la deuxième loi de Newton pour mieux comprendre :
Si l'accélération est nulle (a=0), cela signifie que la vitesse est constante. Par exemple, si on pousse avec une vitesse de 1 m/s, alors cette vitesse sera toujours la même, on ne ralentit pas et on n'accélère pas. Si on remplace \(a\) par 0 dans notre équation, on obtient :
$$F_{R}=m\times 0$$
$$F_{R}=0$$
Donc, peu importe la masse, si l'accélération est nulle, c'est-à-dire si on pousse à une vitesse constante, la force résultante sera nulle. Cela ne veut pas dire qu'il n'y a aucune force appliquée à l'objet, mais plutôt que les différentes forces appliquées s'annulent pour avoir une somme de 0 au final.
$$F_{R}=P-F_{f}=7-7=0$$
En résumé, pour que l'objet soit en MRU, il faut que la vitesse soit constante, donc il faut que l'accélération soit nulle, donc il faut avoir une force résultante nulle, donc la force de frottement doit être égale à la force de poussée, puisqu'elles sont de sens opposé et donc s'annuleront! :D
Si la force de frottement était différente de la force de poussée, cela signifierait que la force résultante (la somme des deux forces) ne serait pas de 0. Par exemple, si la force de frottement était de 6 N, on aurait une force résultante de 1 N appliquée sur l'objet :
$$F_{R}=P-F_{f}=7-6=1$$
Donc, ce ne serait pas un MRU, mais plutôt un MRUA, puisqu'on aurait une petite accélération!
$$F_{R}=ma$$
$$1=5\times a$$
$$\frac{1}{5}= a$$
De plus, si l’objet était initialement déjà en mouvement quand les deux forces s’équilibrent, il va continuer à bouger à cette même vitesse constante, car rien ne vient changer cette vitesse (c’est la première loi de Newton, la loi de l’inertie).
Là où ça peut devenir mélangeant, c’est lorsqu'on part d’un état de repos. Pour qu’un objet immobile se mette à bouger, il faudrait au début qu’il y ait une force résultante non nulle pour lui donner une accélération et ainsi changer sa vitesse de v=0 m/s à v=1 m/s par exemple. Mais, si dès le départ la force de frottement est exactement égale à ta poussée, il restera immobile (v=0 et a=0, donc v reste à 0).
C’est pour ça qu’en pratique, au moment où tu commences à pousser, il y a souvent une petite période d’accélération où la poussée est plus grande que le frottement jusqu’à ce que l’objet atteigne une vitesse constante. Une fois cette vitesse constante atteinte, les deux forces s’équilibrent et on entre en MRU.
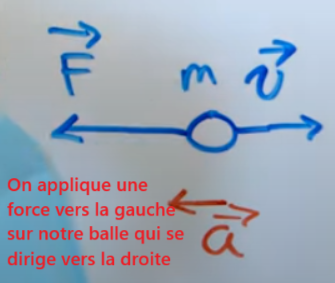
Ensuite, concernant ta seconde question, la balle se déplace dans l’espace à une vitesse initiale constante de 3 m/s vers la droite (donc MRU car vitesse constante → a=0), et on applique ensuite une force constante de 4 N vers la gauche (donc dans le sens opposé à la vitesse).
Puisqu'il n'y a aucune autre force appliquée sur l'objet, la force résultante sera de 4 N vers la gauche.
À ce moment-là, tu t'attendrais à ce que l'objet se dirige alors vers la gauche, n'est-ce pas (puisque tu as une balle qui va vers la droite, tu la tires vers la gauche, et il n'y a aucune résistance car on est dans l'espace, donc elle devrait aller logiquement dans le sens de ta poussée)? Donc, la vitesse, qui était de v= 3 m/s (positive donc vers la droite), devrait changer pour devenir v= -3 m/s (négative donc vers la gauche) (ou un autre nombre, l'important c'est que la vitesse devienne négative pour aller vers la gauche), tu es d'accord? En d'autres mots, on veut passer de v=3 à v=-3, on a donc besoin d'un a non nul pour faire ce changement de vitesse!
On a besoin d'une décélération (diminution de vitesse) pour passer de v=3 à v=0. La variable \(a\) sera négative pour être de signe opposé à la vitesse qui est positive (si l'accélération est de signe opposé à la vitesse alors on a une décélération). De plus, on a besoin d'une accélération (augmentation de vitesse) pour passer de v=0 à v=-3. La variable \(a\) sera aussi négative ici, car on veut être de même signe que la vitesse qui est maintenant négative.
Petit résumé pour t'aider :
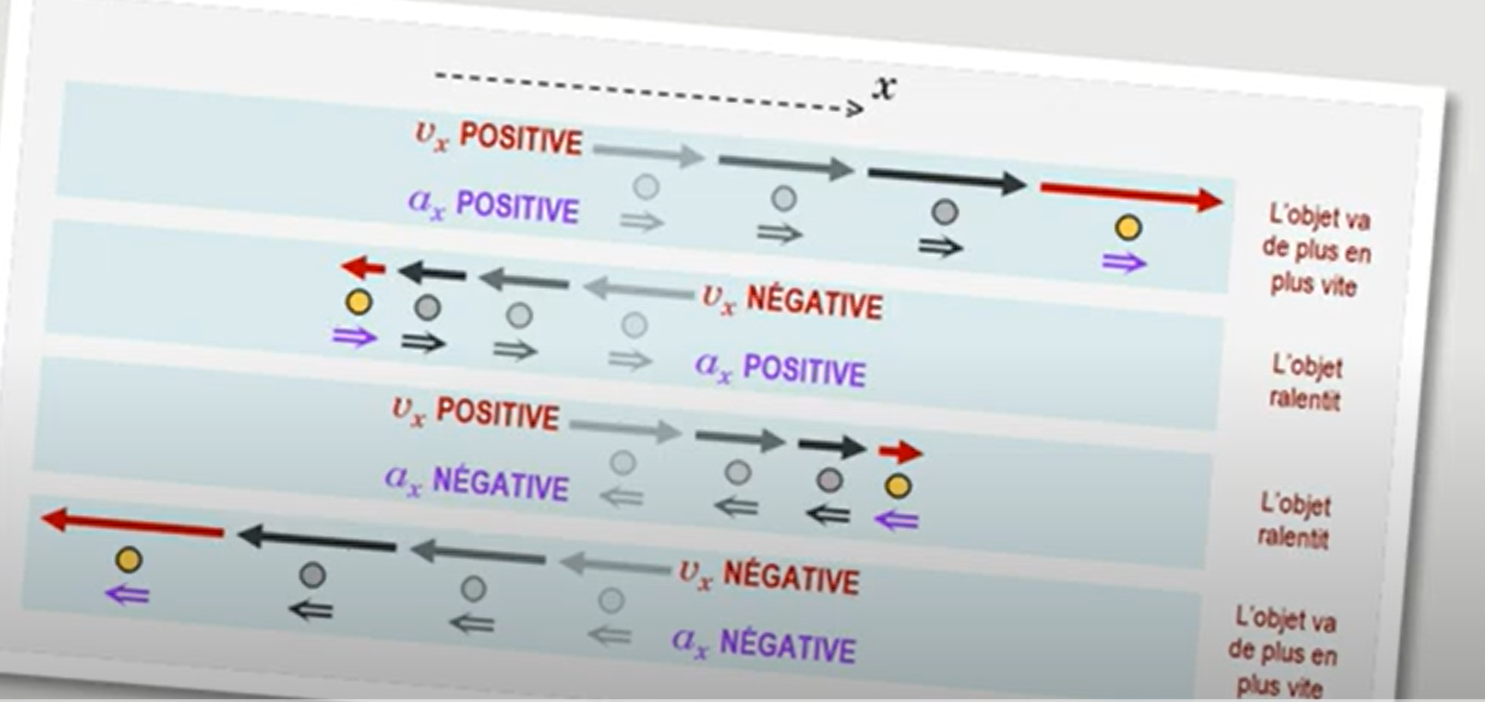
- a et v même signe = accélération, on va plus vite
- a et v signe opposé = décélération, on va plus lentement
- v positif = on va vers la droite
- v négatif = on va vers la gauche
Cette vidéo sur le sujet pourrait t'aider : Les signes de la vitesse et de l'accélération (Physique XXI Tome A Section 1.5) - YouTube
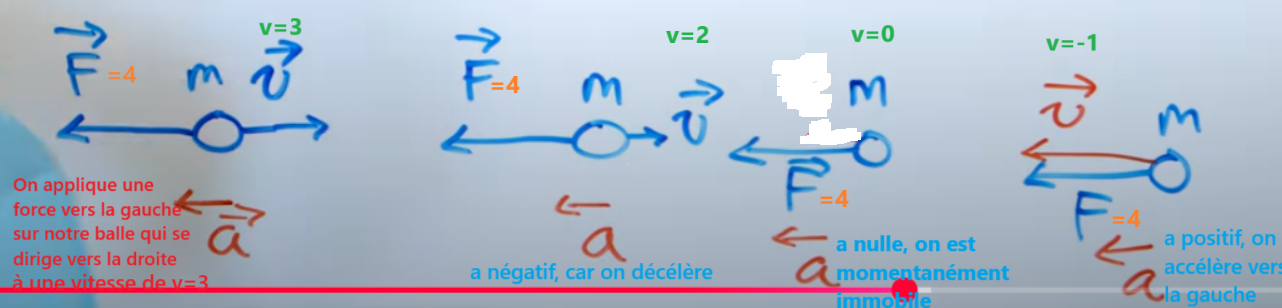
En d'autres mots, pour passer de v=3 à v=-3, on décélère pour changer de sens et atteindre v=0, la balle s'arrête momentanément donc v=0, puis on accélère pour atteindre v=-1, v=-2, puis v=-3 etc.
Tant que la force de poussée sera appliquée, il y aura une force résultante non nulle, et donc une accélération. Si on arrête d'appliquer la poussée à un moment donné, l'accélération deviendra nulle et la vitesse sera constante et égale à celle au moment où la poussée a été arrêtée.
Pour mieux comprendre, tu peux t'imaginer le superhéros Hulk essayer de tirer une corde vers la gauche reliée à une voiture en mouvement vers la droite. Puisque la voiture est lourde, il aura de la difficulté à faire changer de direction le mouvement de la voiture. Au début, il tire, la voiture se met à ralentir progressivement mais est toujours en mouvement vers la droite (donc v positif) (on peut s'imaginer Hulk détruire le sol avec ces pieds à ce moment-là tellement il tire fort), puis la voiture se met enfin à aller vers la gauche grâce à la poussée de Hulk et il se met à courir (donc v négatif). Lors du petit moment de transition où la voiture passe d'un mouvement vers la droite à un mouvement vers la gauche, la vitesse est nulle.
C'est un peu la même chose pour le cas de cette balle dans l'espace!
Voilà! J'espère que c'est plus clair pour toi! Reviens nous voir si tu n'es pas sûr de comprendre quelque chose! :)
Question
Est-ce que les élèves ont droit à un lexique maths pendant l'epreuve du ministère et si oui, comment est déterminé les contenu permis dans le lexique?
Merci d'avance
Question
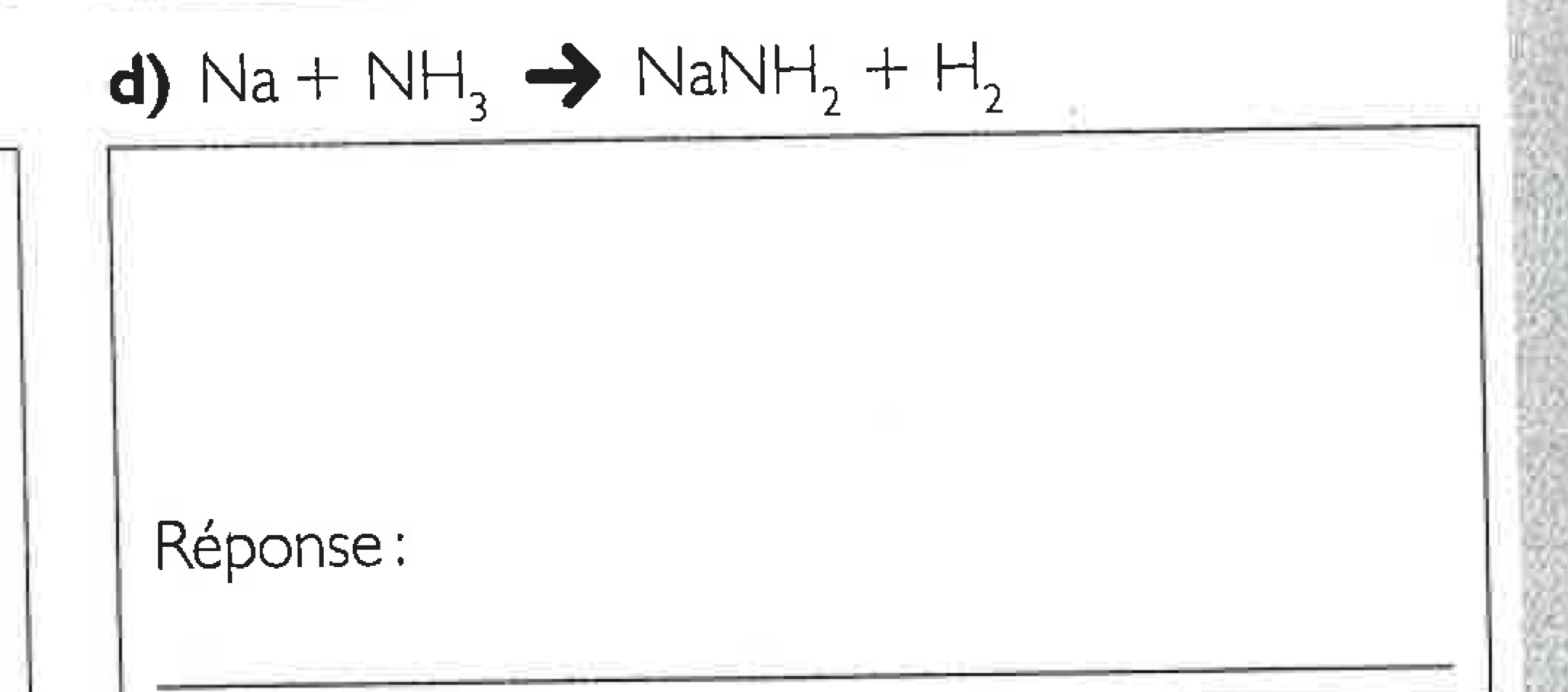
I need to balance this chemical equation and show my work but I’m getting a lot of fractions and I don’t think it’s right, could you help me figure it out?
Re: Question
Salut!
L'objectif est d'isoler x complètement, puis, de représenter l'inéquation sur une droite numérique. Par exemple, si nous avons x < 3, alors l'ensemble [-∞, 3[ sera représenté sur la droite numérique.
Isolons x dans :
$$ \frac{10}{x-3}+2 ≥ 8 $$
Nous allons commencer par déplacer les constantes d'un côté :
$$ \frac{10}{x-3}+2 -2≥ 8-2 $$
$$ \frac{10}{x-3} ≥ 6 $$
Puis nous pouvons affecté un exposant négatif dans chaque côté de l'équation afin de ramener notre variable x au numérateur, OU multiplier par (x-3) de chaque côté. Nous allons faire cette dernière méthode.
$$(x-3) • \frac{10}{x-3} ≥ 6 • (x-3) $$
$$10 ≥ 6 • (x-3) $$
Nous allons diviser par 6 des deux côtés :
$$ \frac{10}{6} ≥ \frac{6 •(x-3) }{6} $$
$$ \frac{5}{3} ≥ x-3 $$
Ensuite, nous allons déplacer la constante 3 de l'autre côté :
$$ \frac{5}{3} + 3 ≥ x $$
$$ \frac{14}{3} ≥ x $$
Nous obtenons donc 4,667 ≥ x, ou encore x ≤ 4,667.
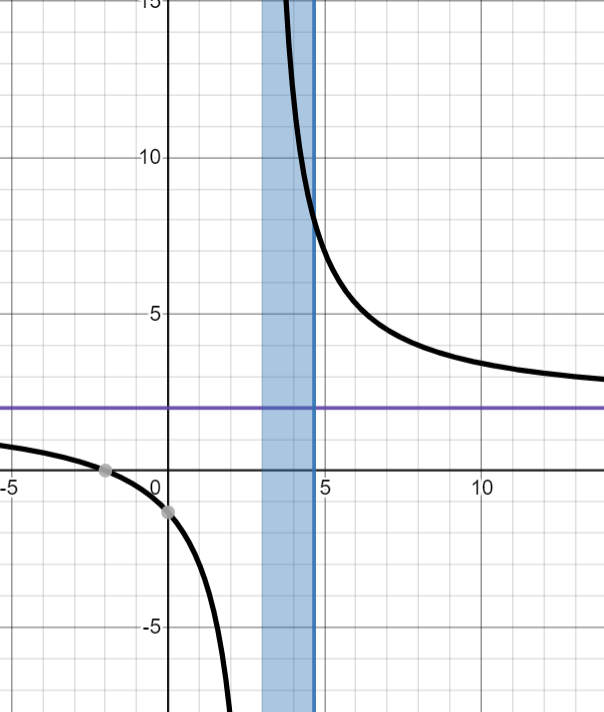
Ensuite, pour déterminer l'ensemble solution, nous allons tracer le graphique de cette inéquation :
Les asymptotes sont tracées en couleur.
En regardant le graphique, on peut déterminer que l'ensemble-solution est ]3; 4,667].
L'intervalle est ouvert en x puisque cette valeur correspond à l'asymptote verticale, et la fonction rationnelle n'y touchera jamais.
Il ne restera plus qu'à représenter ce résultat sur une droite numérique à l'aide d'un point ouvert et d'un point fermé.
Voici des fiches sur cette notion qui pourraient t’être utiles :
- https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/resoudre-une-equation-ou-une-inequation-rationn-m1400#
- https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/le-demi-plan-et-l-ensemble-solution-m1534
N'hésite pas si tu as d'autres questions :)
Re: Question
Salut!
Ta question a été répondue ici :
J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions!
Anthony B.
Re: Question
Salut MoustiqueExtraordinaire4798,
Merci pour ta question !
L'évolution, c'est le changement des espèces au fil des générations. Dans une espèce, les individus les mieux adaptés à leur environnement ont plus de chance survivre et de se reproduire, leur permettant ainsi de transmettre leurs caractéristiques avantageuses à leurs bébés. Par exemple, les girafes avec des cous plus longs pouvaient mieux atteindre la nourriture et ont eu plus de descendants, ce qui a rendu les longs cous plus fréquents avec le temps. C'est la sélection naturelle qui guide l'évolution !
Je t'invite à consulter cette fiche pour en savoir davantage:
J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions !
Anthony B.
Re: Question
Salut OliveOrange9027,
Merci pour ta question!
La vitesse instantanée est la vitesse à un moment précis. Pour la trouver, tu peux utiliser le graphique de la vitesse en fonction du temps s'il est présenté, sinon tu peux utiliser celui de la position en fonction du temps si tu es dans le MRU. La pente de ce graphique correspond à la vitesse de ton objet. Dans certaines situations, cette valeur est mentionnée dans l'énoncé de problème!
Aussi, tu peux utiliser les formules du MRUA pour y arriver, si tu cherches la vitesse instantanée à un temps t, la vitesse finale correspond à cette valeur!
Voici une fiche à ce sujet si tu veux en savoir davantage:
J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions!
Anthony B.
Re: Question
Salut OliveOrange9027,
Merci pour ta question!
La vitesse moyenne est la vitesse moyenne lors de l'ensemble d'un mouvement. Par exemple, si une automobile roule à 5 m/s durant 10 s et ensuite sa vitesse monte à 15 m/s durant 10 s, sa vitesse moyenne durant son trajet était de 10 m/s.
La vitesse instantanée est la vitesse à un moment précis, par exemple durant la 2e seconde de son mouvement l'automobile roulait à 5m/s.
Tu pourras trouver des informations supplémentaires en cliquant sur le lien suivant :
J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions!
Anthony B.