Best Of
Re: Question
Bonjour OrnithorynqueOptimiste8838,
Il est normal d'avoir de la difficulté. Je vais donc te guider.
Voici un document qui devrait t'aider :
https://www.alloprof.qc.ca/fr/eleves/bv/francais/la-structure-d-un-texte-descriptif-f1439
Pour faire un bon texte descriptif, tu dois t'assurer de bien structurer ton texte en t'assurant de la présence de l'introduction, du développement et la conclusion. De plus, pour t'assurer de faire un bon texte, assure toi d'avoir des aspects et des sous-aspects tout en respectant un plan préparé qui mettra en valeur le sujet principal.
Je te conseillerais donc de faire une recherche à l'aide d'un plan que tu vas concevoir, puis de choisir les sujets et sous-aspects que tu veux aborder.
Au plaisir de t'aider, et n'hésite pas à revenir si tu as d'autres questions !
Bon travail,
OnyxIntergalactique1301
Re: Question
Bonjour SoleilInoubliable8340,
Merci beaucoup pour ta question! Bon poisson d’avril à toi également! 🐠
Tout d’abord, il existe des propriétés caractéristiques et des propriétés non caractéristiques. Les propriétés caractéristiques sont celles qui sont propres à une substance. La température d’ébullition ou la masse volumique en sont des exemples.
Ensuite, les propriétés non caractéristiques ne sont pas propres à une seule substance. On parle alors de la masse, du volume ou encore de la température. Voici une fiche qui pourrait t’aider :
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!
Re: Question
Bonjour SoleilInoubliable8340,
Voici un document qui devrait t'aider :
https://www.alloprof.qc.ca/fr/eleves/bv/sciences/sciences-les-proprietes-de-la-matiere-s1002
Une propriété peut être physique (observée sans changer la nature de la substance) ou chimique (décrivant le comportement lors d'une réaction chimique). De plus, les propriétés peuvent être caractéristiques (uniques à une substance) ou non caractéristiques (communes à plusieurs substances). Dans le corps humain, de nombreuses substances se présentent sous forme de mélanges, souvent des solutions, dont l'étude des propriétés est intéressante.
Il y a également une vidéo pour te guider.
Au plaisir de t'aider, et n'hésite pas à revenir si tu as d'autres questions !
Bon travail,
OnyxIntergalactique1301
Re: Question
Bonjour,
Ton graphique représente la température moyenne à Paris.
De ce fait, si tu lis la température inscrite pour ton mois d'avril, tu obtiendras la température moyenne en avril.
Bonne journée :)
Re: Question
Bonsoir, JujubeCalme1293!
Merci d'utiliser la zone! Je peux certainement te donner quelques techniques de mémorisation.
Un élément clé pour apprendre par coeur est la répétition. Ceci te permettra d'approcher le jour de tes évaluations avec confiance.
Je te suggère donc d'étudier plusieurs fois les textes et les mouvements pendant des périodes d'environ 30 minutes et de prendre une pause après.
Faire de courtes périodes d'études pour donner un peu de repos à ton cerveau lui permettra d'emmagasiner l'information dans la mémoire à long terme.
Tu peux aussi te pratiquer seule et à voix haute. Imagine qu'un auditoire te fait face. Pratique aussi tes mouvements. Mémorise le plus possible l'ordre dans lequel tu devras présenter ton contenu.
N'attends pas à la dernière minute! Plus que tu es préparé, plus tu auras mémorisé tes textes et mouvements.
Si tu le souhaites, tu peux aller lire ces trucs pour la préparation d'un exposé oral :
Tu pourras utiliser mêmes techniques pour ton cours d'Art dramatique.
Je te souhaite une bonne préparation et n'hésite pas si tu as d'autres questions!
Iris :)
Re: Question
Bonjour,
Pour résoudre ce problème, sépare ta figure en plusieurs figures différentes.
Ici, nous avons premièrement les 6 côtés de ton prisme (des rectangles).
Puis, nous avons deux cercles (les bases du cylindre) et l'aire latérale de ton cylindre (un rectangle).
Pour avoir l'aide de ton solide, tu dois commencer par calculer l'aire des différents côtés de ton cube. N'oublie pas de soustraire l'aire de tes deux cercles.
Par la suite, il te suffit d'ajouter l'aire latérale de ton cylindre pour obtenir ton aire totale.
Voici un lien utile :
Bonne journée :)
Re: Question
Bonjour,
Merci pour ta question!
Le pH est une mesure qui permet de déterminer le degré d’acidité ou de basicité d’une solution. On utilise l'échelle de pH pour comparer le caractère acide, neutre ou basique des solutions. L'échelle va de 0 à 14. Une solution possède un pH acide lorsqu'il est inférieur à 7. Lorsqu'il est égal à 7, on dit que la solution est neutre. Enfin, lorsque le pH est supérieur à 7, on dit que la solution est basique. C'est de cette manière que nous sommes en mesure de comparer les solutions.
Pour le papier tournesol, il permet de déterminer le caractère basique ou acide d'une substance. Un acide rougit le papier tournesol bleu, tandis qu'une base bleuit le papier tournesol rouge.
Voici une fiche sur le pH et une autre sur l'acidité et la basicité :
J'espère t'avoir aidé. N'hésite pas si tu as d'autres questions!
Re: Question
Salut!
Je t'invite à consulter cette fiche : Les solides | Secondaire | Alloprof
Tu y trouveras des liens menant vers différentes notions reliées aux solides, et il y a quelques exercices si tu descends jusqu'en bas de la page de certaines de ces notions.
Bonne pratique! :)
Re: Question
Salut!
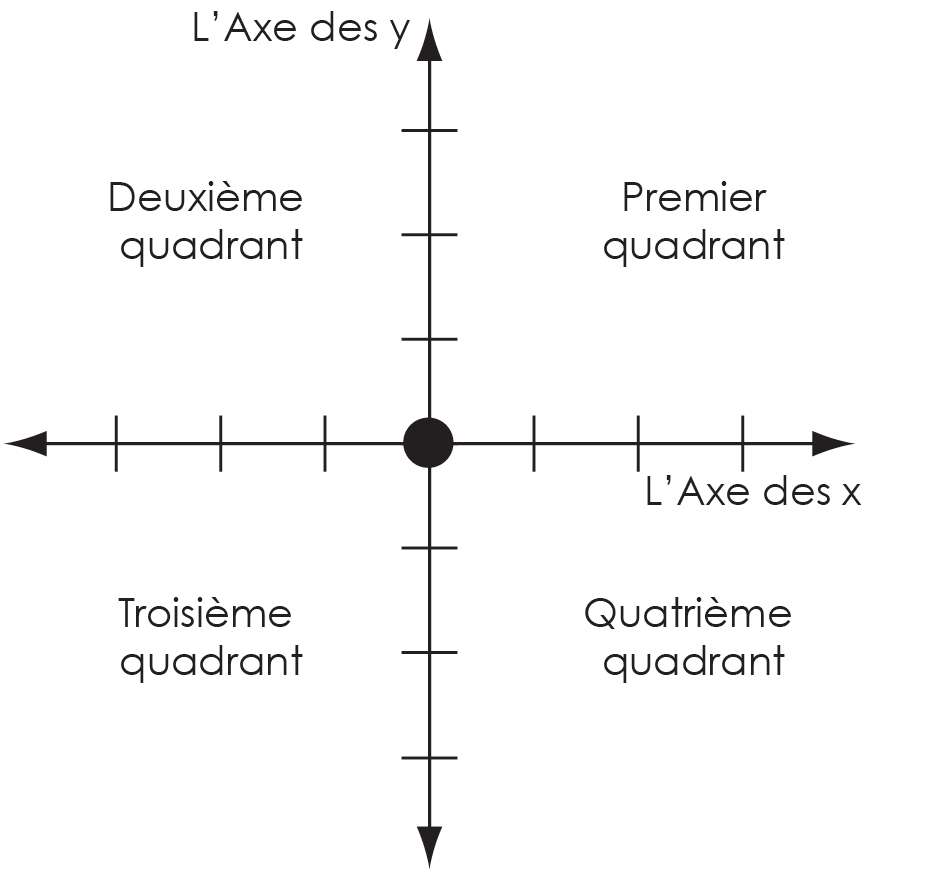
Dans un plan cartésien, les quadrants sont les quatre sections formées par l'axe des x et l'axe des y.
Le premier quadrant est celui en haut à droite, le deuxième est en haut à gauche, le troisième est en bas à gauche, et le quatrième est celui en bas à droite :
Voici une fiche qui pourrait t'être utile : Le plan cartésien | Primaire | Primaire | Alloprof
J'espère que c'est plus clair pour toi! :)