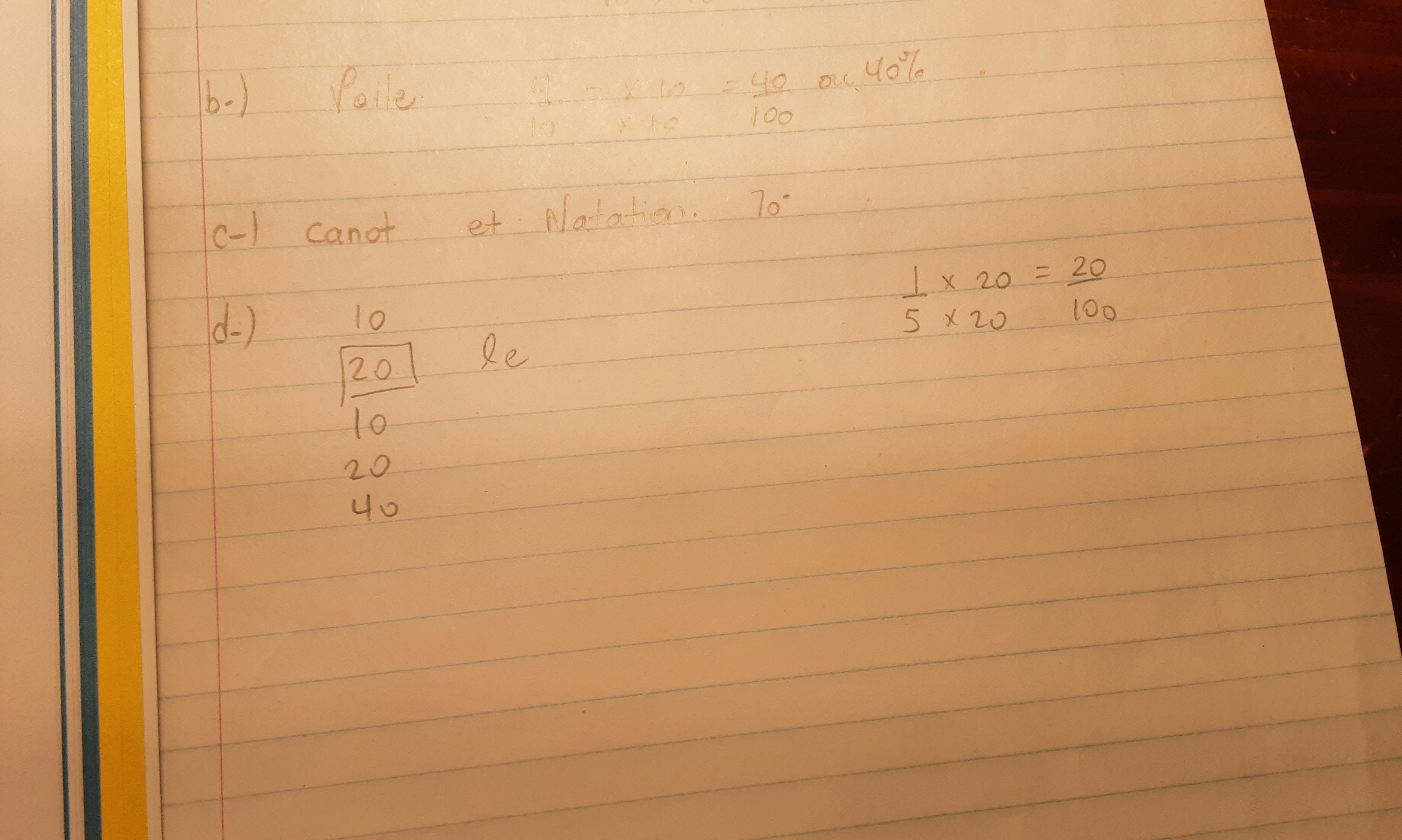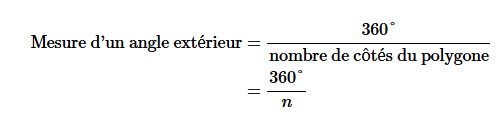Best Of
Question
Bonjour Sandrine et Katia,
On me demande quelle activité an singulier le 1/5 des jeunes préfère?
- 1/5 est égal à 20/100
Donc j'aurais le canot et la natation?
Re: Question
Salut!
Si sa peut t'aider, les mélanges est une association de plusieurs substance qui ne provoquent pas de réactions chimique entre elles
Re: Question
Salut!
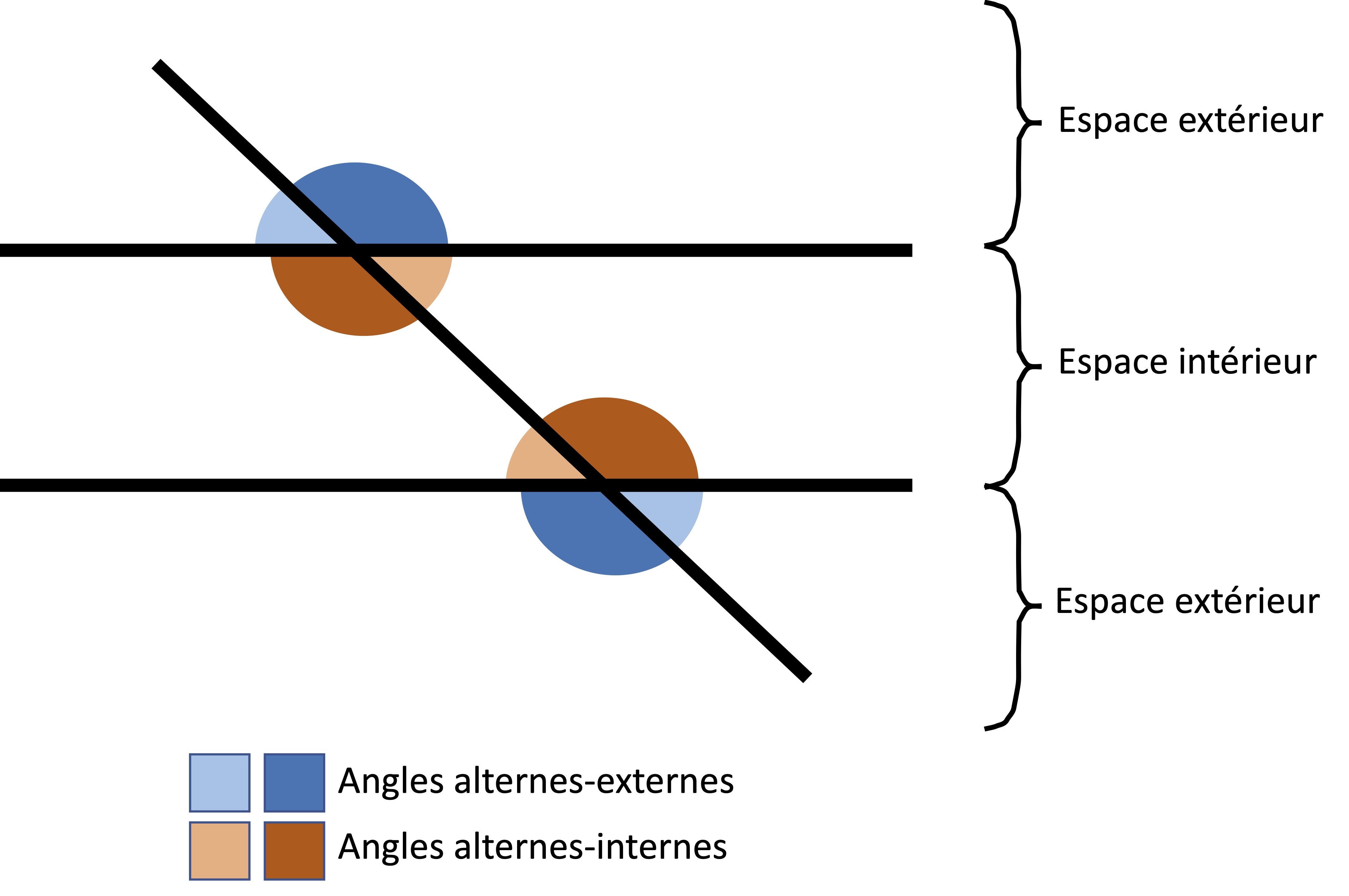
Les angles alternes-internes et les angles alternes-externes sont formés par une droite sécante coupant deux droites parallèles. Ces angles sont situés de part et d'autre de cette droite sécante (un angle à gauche de la droite sécante, et l'autre à droite).
La différence est que les angles alternes-internes sont dans l'espace à l'intérieur des droites parallèles, ils sont donc dans l'espace interne, tandis que les angles alternes-externes sont situés dans l'espace à l'extérieur des droites parallèles, dans l'espace externe.
En bref, alternes-internes = à l'intérieur des droites, alternes-externes = à l'extérieur des droites.
Voici une fiche sur cette notion qui pourrait t'être utile : Les relations entre les angles | Secondaire | Alloprof
Si tu as d'autres questions, on est là! :)
Question
Qu'est ce que je peux utiliser pour reviser mon histoire de secondaire 4
Re: Question
Bonjour IguaneOptimiste1643
Bonne question! 😎
Je dirais que les synonymes que tu as donné sont juste!
Cependant, je te suggère d'aller en parler avec le prof s'il ne t'accorde pas le point, car vue que c'était bien un examen sur les tremblements de terre, peut-être qu'il cherchait vraiment le synonyme: tremblement de terre.
Par contre, les synonymes que tu as nommé sont bien choisis! 😄
En effet, séisme qui signifie "résulte de la libération d'énergie accumulée par les déplacements et les frictions des différentes plaques de la croûte terrestre"
et secousse: "Mouvement brusque".
Ce sont des définitions qui décrivent bien un tremblement de terre! Bravo!
Si tu as d'autres questions n'hésite pas à revenir sur la Zone d'entraide! 😎
KiwiChouette3743
Re: Question
Salut!
Tu dois utiliser cette formule :
Si l'angle extérieur est de 36 degrés, alors on doit trouver n dans cette équation :
$$36=\frac{360}{n}$$
Je te laisse faire le calcul. Si tu as besoin d'aide pour résoudre l'équation, reviens nous voir! :)
Re: Question
Salut !
Aucun notion n'est indispensable pour reproduire une expérience. Aussi, le niveau scolaire n'est pas forcément problématique pour comprendre des concepts plus poussés. Il est toujours possible de voir ces notions en surface avec une compréhension suffisante pour les besoins de l'expérience.
Par exemple, pour la poussée d'Archimède, voici une vidéo qui peut simplifier la compréhension.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Bonjour ElfeTimide233
Merci pour ta question! 😎
Bravo, tu as bien trouvé le verbe et l'adjectif! 😄
Cependant, belle essaie, tu as essayé de trouver l'adverbe de séduire en lui donnant la terminaison "...ment", mais ce mot n'existe pas!
Donc, séduire n'a pas d'adverbe!
Je te suggère d'aller voir les différents adverbe possible dans cette fiche:
Si tu as d'autres questions, n'hésite pas à revenir sur la Zone d'entraide!
Bon travail! 😎
KiwiChouette3743
Re: Question
Salut GalaxieSigma4570!
Merci pour ta question. :)
Si l'on reprend sa définition, la disparité représente l'inégalité entre deux choses.
Si l'on applique à la répartition des richesses, la disparité fait référence au fait que la situation économique est très différente d’un pays à un autre. Certains pays ont accès à certaines ressources que d’autres n’ont pas. Ainsi, selon ses ressources et les infrastructures en place, chaque pays se concentre sur des domaines économiques en particulier, comme les mines, les pêcheries, l’agriculture, les services, les hautes technologies ou encore la production manufacturière. Cela fait en sorte que le niveau de richesse de certains pays dans le monde est beaucoup plus élevé que celui d’autres pays.
Si tu souhaites obtenir plus d'informations, je t'invite fortement à consulter cette fiche explicative portant sur ce sujet! :D
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane :)