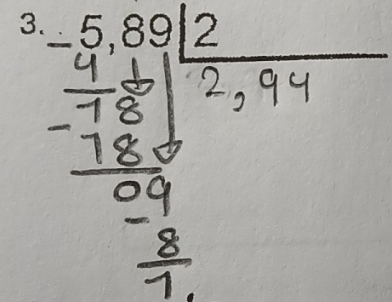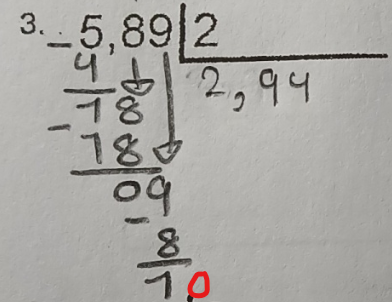Best Of
Re: Question
Salut!
Le verbe poignarde s'accorde ici avec suivi, donc à la 3e personne du singulier. Cependant, je te conseillerais de revérifier la structure de ta phrase, ou d'enlever le déterminant un.
Si tu as d'autres questions, n'hésite pas! :)
Re: Question
Salut GalaxieJaune4428 😁
Merci pour ta question!
Oui, à peu près comme dans la bd!
Jules César était un homme politique, un militaire et un avocat romain. Considéré comme un stratège et un tacticien habile, il agrandit considérablement le territoire romain en faisant notamment la conquête de la Gaule.
Pendant ce temps, la population de certaines provinces romaines se révolte. César part alors en province pour mettre fin à la guerre civile qui sévit. De retour à Rome, César, victorieux, se proclame dictateur à vie. Peu de temps après, il se fait assassiner par des membres du Sénat, dont le fils de sa maitresse, Brutus, qui lui porte le dernier coup. Dix-sept ans plus tard, la République romaine disparait pour laisser place à l'Empire romain. Octave, son fils adoptif, en devient le premier empereur et il divinise Jules César.
Au Moyen Âge, il est considéré comme une des neuf grandes figures historiques du monde (Neuf Preux). Si les jeux spectaculaires qu'il a commandés, et même parfois organisés, ont grandement contribué à sa notoriété, Jules César est surtout reconnu pour ses nombreuses conquêtes territoriales et pour ses réformes. Les empereurs romains qui suivirent reprirent le nom de César à titre honorifique.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Bonjour GalaxieJaune4428, merci pour ta question !
Le rôle d'empereur et de roi est très similaire, il y a juste une grande différence.
Un roi va régner sur un royaume et un empereur sur un empire.
Ce qui distingue un royaume d'une empire, c'est leur taille. Un royaume est à l'échelle d'un pays alors qu'un empire regroupe plusieurs pays voire un continent entier sous son pouvoir.
Donc l'empereur est un rôle plus prestigieux que celui de roi.
N'hésite pas à nous écrire si tu as d'autres questions !
Re: Question
Salut!
Je crois que oui malheureusement 😣 J'ai contacté notre équipe de soutien technique, le jeu ne devrait pas tarder à être de retour, je te tiendrais au courant juste ici!
A+ 🙂
Re: Question
Bonjour!
Nous avons plusieurs fiches intéressantes à lire dans le cadre du Mois de l'histoire des Noirs! :D
En voici quelques-unes :
La lutte des Noirs : de l'esclavage à la présidence
La lutte contre le racisme
Martin Luther King
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Bonjour FraiseRose4867,
Merci pour ta question :)
Tu as la bonne réponse pour les deux exercices :) On peut les résoudre de deux manières. Premièrement, et c'est ce que tu as fait, on peut simplifier les expressions sous des bases plus simples. Par exemple pour le b), on peut écrire 16/9 sous la forme 4^2/3^2, puis (4/3)^2 et finalement (3/4)^-2. Lorsqu'on le met dans l'équation (3/4)^x=(3/4)^-2, on voit que x=-2.
L'autre option est d'utiliser le logarithme, qui est l'opération réciproque de la notation exponentielle. Par exemple pour résoudre l'équation 2^x=8, on peut utiliser le log qui transforme l'équation en log_2(8)=x, ce qui donne x=3. Si tu veux en apprendre plus sur les logarithmes, je t'invite à consulter la page suivante: https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/les-logarithmes-m1358
N'hésite pas si tu as d'autres questions :)
Sandrine
Re: Question
Salut!
Tout d'abord, voici mes corrections :
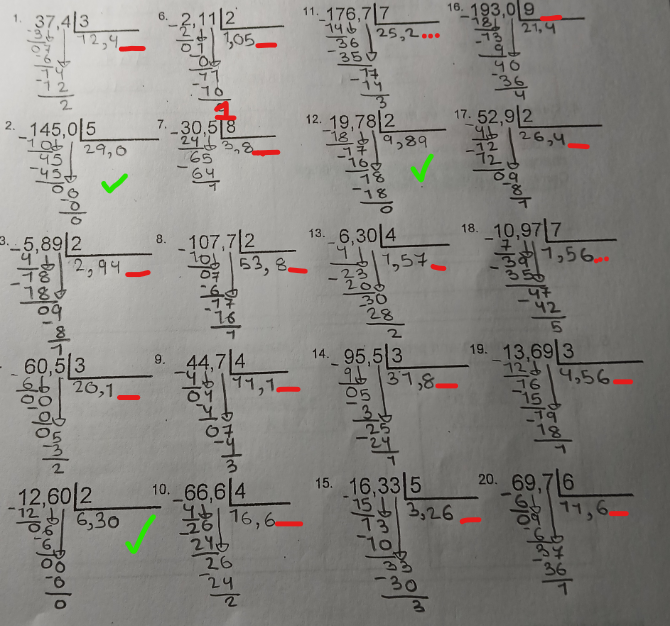
Tes réponses sont toutes les bonnes, mais il manque quelques chiffres après la virgule pour plusieurs.
En fait, lorsque tu fais une division, tu peux obtenir trois types de résultats :
- En nombre décimal avec un certain nombre de chiffres après la virgule (ex. 94,37)
- Un nombre décimal avec une infinité de chiffres après la virgule, et ces chiffres sont aléatoires (ex. 3,19879834782....)
- Un nombre décimal avec un nombre de chiffres infini après la virgule, mais il s'agit du même chiffre ou de la même séquence de chiffre qui se répète (ex. 5,2222222222...). On appelle ces nombres des nombres périodiques.
Ainsi, pour résoudre ces divisions, voici comment je te propose de fonctionner: tu commences par effectuer ta division comme à l'habitude. Lorsque tu es rendu à diviser des chiffres qui sont dans la partie décimale du nombre, si tu obtiens un reste de 0, alors tu as fini ta division, et cela signifie que tu as obtenu un résultat avec un nombre de chiffres précis après la virgule (type #1). Si tu n'as pas un reste de 0, tu continues la division, et ce, en ajoutant un 0 à ton reste. Par exemple, ici :
On a un reste de 1. Nous allons donc ajouter un 0 à droite de ce 1 :
On peut ainsi diviser notre reste de 10 par 2, ce qui nous donne 5. On constate alors qu'on n'a plus de reste, donc la division est maintenant terminée!
La réponse est donc 2,945.
Si on avait encore eu un reste, alors il aurait fallu rajouter un autre 0. Il faut faire cela à chaque fois que l'on a un reste.
Maintenant, le problème, c'est que certains nombres possèdent un nombre infini de chiffres après la virgule. Bien sûr, on ne va pas continuer la division indéfiniment 😆. Si on voit qu'on est rendu à 3 ou 4 chiffres après la virgule et qu'on a toujours un reste, on peut s'arrêter là et conclure qu'on a un nombre du type 2 dont je te parlais précédemment, c'est-à-dire un nombre avec un nombre infini de chiffres aléatoires après la virgule. Pour écrire ce nombre, tu peux mettre trois petits points à la fin pour montrer qu'il continue jusqu'à l'infini (ex. 3,492...).
Cependant, si on constate qu'on obtient le même chiffre plusieurs fois de suite, alors on conclut qu'il s'agit d'un nombre périodique (type 3), et donc on peut mettre une petite barre en haut du chiffre qui se répète (ex. 4,66666 = \(4,\overline{6}\)).
Je te laisse corriger le tout avec ces indices. Reviens nous voir si tu as besoin d'aide! :)
Re: Question
Bonsoir GalaxieSigma4570!
Excellente observation que tu as faite! Elle m'a obligé à faire quelques vérifications. Effectivement il y a une incohérence à écrire dans la partie 3 que le ΔH2 est de - 484,2 KJ/mol alors qu'en réalité on a simplement doublé la valeur de la chaleur molaire.
Comme les équations intermédiaires concernent que des réactions produisant une mole de CO2 (réaction 1 et 3) et une mole de H2O (réaction 2), il n'aurait pas été nécessaire d'écrire les ΔH en kJ/mol.
Ainsi les modifications apportées à l'étape 3, feraient plus de sens.
Seulement il faut bien vérifier à l'étape 4 que le ΔH total correspond bien à une valeur exprimée en kJ/mol, ce qui pourrait amener un ajustement à la valeur obtenue. Exemple: si la réaction globale donnait 2 moles de CH4 au lieu d'une seule alors il aurait fallu diviser en 2 la valeur du ΔH total pour l'exprimer en kJ/mol.
Bravo pour ta remarque judicieuse! J'en prends note et suggérer des améliorations à cet exemple que l'on retrouve dans notre fiche sur la loi de Hess.
Merci à toi! :-)
ThonLucide8631
Re: Question
Salut!
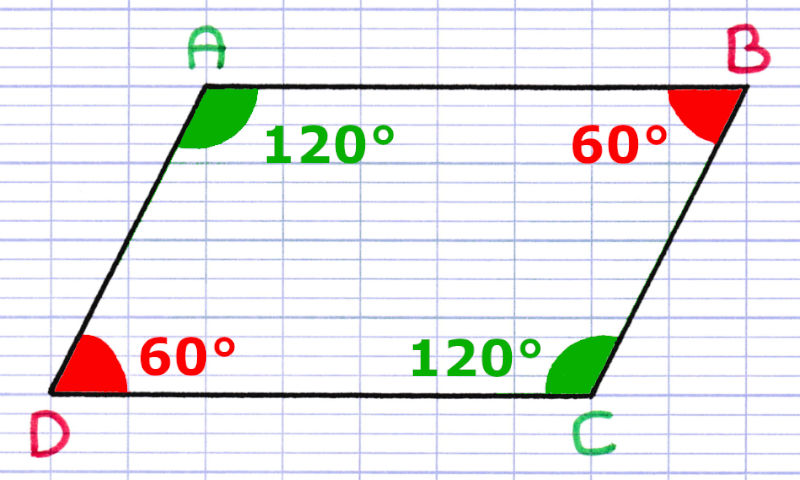
Un angle consécutif à un autre est un angle qui a un côté du polygone en commun. En d'autres mots, ce sont des angles "voisins".
Par exemple, l'angle A et l'angle B sont consécutifs, puisqu'il partage le côté AB. Cependant, l'angle A n'est pas consécutif à l'angle C, puisqu'ils ne partagent aucun côté en commun. L'angle A est également consécutif à l'angle D. Ainsi, l'angle A a pour angle consécutif les angles qui lui sont voisins, soit A et B.
Voici des explications supplémentaires qui pourraient t'intéresser :
- Bonjour, je ne comprends toujours pas ce qu'est un angle con — Alloprof
- Bonjour, <br> Quelle est un angle consécutif et quelle est une — Alloprof
J'espère que c'est plus clair pour toi! :)