Best Of

Salut FramboiseAutonome2366 !

Pour calculer l'aire, tu as besoin de quelques informations.

Tout d'abord, tu as besoin de tes formules.

Ensuite, tu as besoin d'avoir les différentes mesures pour utiliser tes formules.

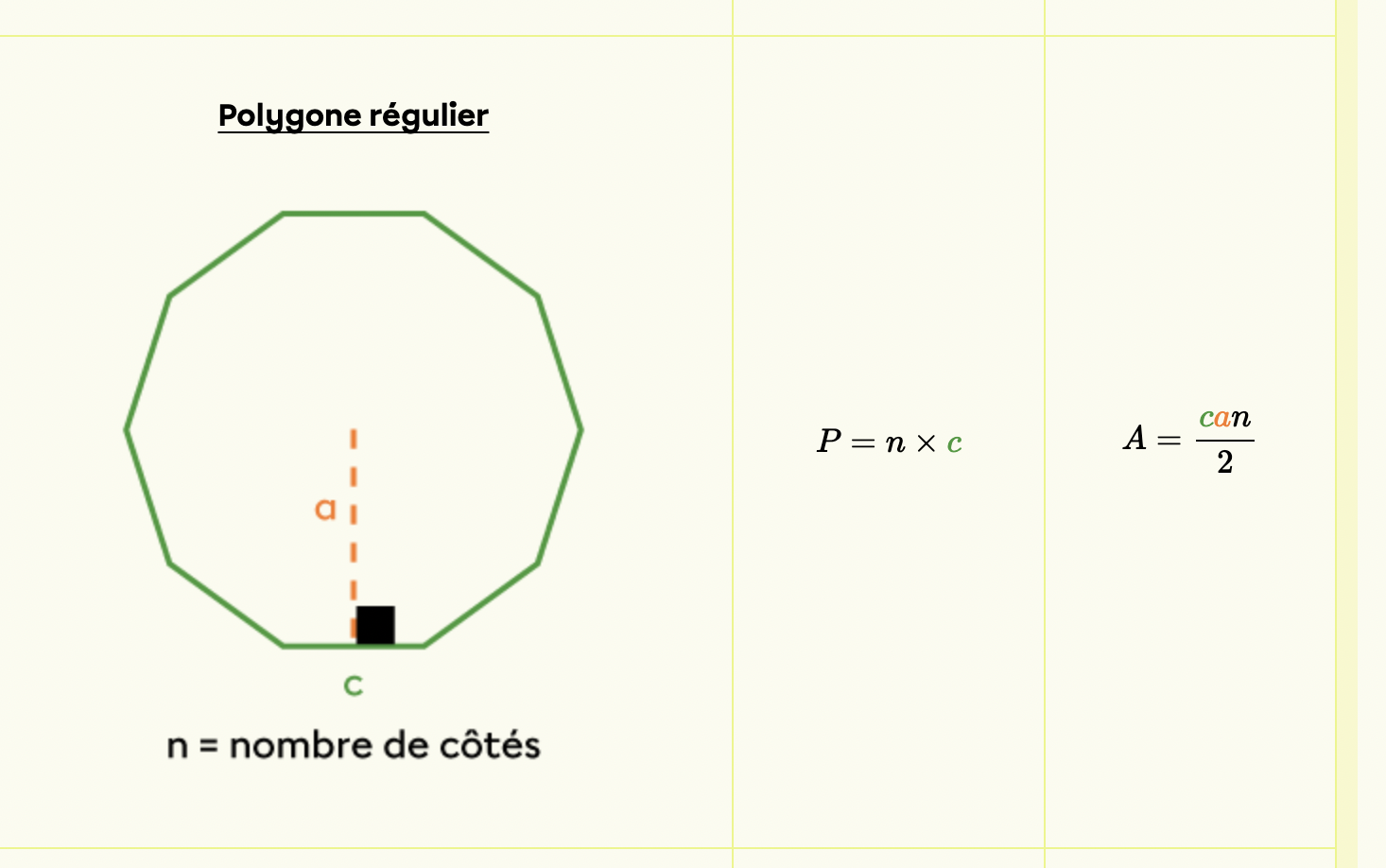
Voici une fiche où on trouve toutes les formules de l'aire des figures planes :

La mesure à l'extérieur ici représente la mesure d'un côté.

La mesure à t'intérieur représente ton apothème (a).

Par exemple :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ici tu vois que pour calculer l'aire du polygone régulier, tu dois faire la formule de droite.

J'espère que cela t'aide.

N'hésite pas à repasser nous voir au besoin ! :)

Salut FramboiseAutonome2366 !

Merci de faire appel à nos services. :)

Bonjour ! La formule (n−2)×180 pour calculer la somme des angles intérieurs d'un polygone est basée sur une division du polygone en triangles.

Un triangle (3 côtés) : il est déjà un seul triangle, donc n−2 = 3−2 =1 triangle.

Un quadrilatère (4 côtés) : il peut être découpé en 2 triangles, n−2 = 4−2 =2 triangles.

Un pentagone (5 côtés) : il peut être découpé en 3 triangles, donc n−2 = 5−2 =3 triangles.

Chaque triangle a une somme des angles intérieurs égale à 180°. Cela est une propriété géométrique fondamentale (qui s'applique toujours).

En découpant le polygone en n−2 triangles, la somme des angles intérieurs du polygone est donc égale à la somme des angles des n−2 triangles.

Voici une fiche qui parle de la formule pour trouver la somme des angles intérieurs d'un polygone :

Voilà ! J'espère que cela répond à ta question.

N'hésite pas à repasser au besoin. :)

À bientôt !

Bonjour,

Pour résoudre ce problème, tu dois remarquer que tes deux coccinelles se déplacent selon une fonction quadratique.

Visite ce lien pour comprendre comment trouver la règle de chacune de tes deux fonctions : 

S'il y a une notion que tu ne comprends pas, n'hésite pas à venir poser tes questions ! Cela nous ferait plaisir de t'aider :)

Une fois que tu auras trouvé tes deux fonctions, égalise-les et trouve le ou les points de rencontre.

Bonne journée :)

Tu peux dessiner 6 points sur une feuille et en rajouter 2 de plus, compte les et tu auras ta réponse !

Salut,

Merci d'utiliser la zone d'entraide.

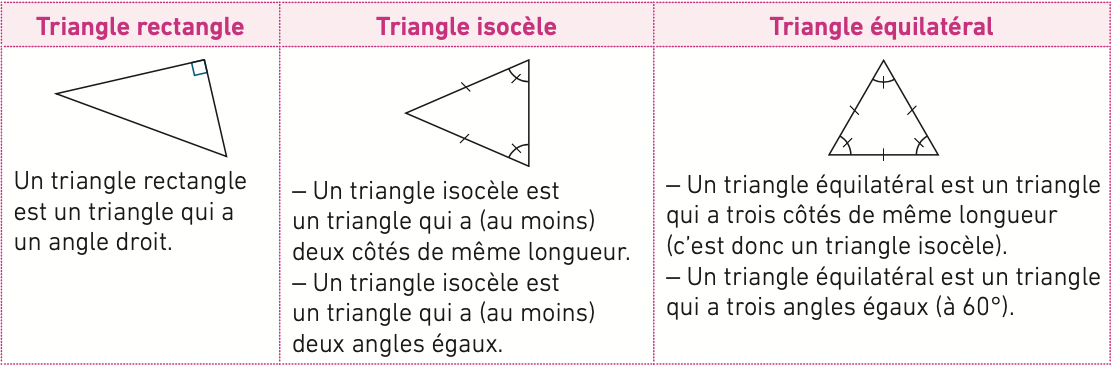
Un triangle isocèle possède 2 côtés de même mesure et 2 angles égaux, tandis qu'un triangle scalène ne possède aucun côté de même mesure et aucun angle égaux. En d'autres mots, un triangle scalène possède trois côtés de différentes mesures et trois angles de différentes mesures.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici une fiche sur cette notion qui pourrait t'être utile : 

En espérant t'avoir aidé,

Bonne journée,

Karen

allo je peu t'aider

voici une image qui peut aider

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

BONNE JOURNÉE A TOI ANGUILLENOBLE1305

Bonjour PapillonOptimiste!

Je vais te guider pour t'aider à trouver la réponse à ta question.

1. Avant tout, essaie de dessiner un esquisse du solide développé. Cela t'aidera a visualiser ou chaque mesure devrait se trouver.
2. On doit trouver l'aire du base (l'octogone). On sait que le perimetre mesure 80 cm et qu'il y a 8 cotes dans un octogone. Donc, on effectue la division suivante: 80cm/8 = 10 cm afin de savoir la mesure d'un de ses cotés. On sait que l'apothème mesure 12 cm. On sait aussi que dans un octogone, il y a 8 triangles identiques. On peut donc utiliser ces données pour trouver l'aire de d'un triangle et le multiplier par 8 afin de trouver l'aire de l'octogone/le base du pyramide.
3. On sait que A totale = A base + A latérale. Donc, on sait que A latérale = A totale - A base
4. Ensuite, sachant que l'aire latérale est composé de 8 triangles identiques, on peut diviser l'aire latérale par 8 afin de savoir l'aire d'un de ces triangle.
5. Finalement, il s'agit simplement d'isoler l'apotheme du pyramide avec les autres donnees que nous savons (l'aire d'un des triangle le base d'un triangle s'agit d'un cote de loctogone) et la formaule de l'aire d'un triangle: A = (b x h)/2.

Voici un lien qui pourrait aussi t'aider avec ce type de question: L'aire et le volume des solides | Secondaire | Alloprof

N'hesite pas à revenir nous revoir si tu as d'aitres questions et bonne chance!

OpalePratique5921