Best Of

Salut!

Tout d'abord, tu dois bien comprendre ce qu'est une asymptote. Une asymptote est une ligne droite vers laquelle une courbe se rapproche de plus en plus sans jamais la toucher, et ce, même si la courbe continue à s'étendre à l'infini. En d'autres mots, l'asymptote est comme une sorte de "limite" pour la courbe.

Mathématiquement, pourquoi y a-t-il une asymptote? Tout simplement parce qu'il y a une valeur que l'on ne pourra jamais atteindre selon la règle que l'on a.

Par exemple, si on a \(f(x)=2^x\), on sait que l'asymptote est de y=0. Pourquoi? Parce qu'il n'y a aucune valeur de x qui nous permet d'obtenir un y=0. Faisons le test :

$$0=2^x$$

Il faudrait être capable de résoudre cette équation. Si on réussit, alors il n'y aurait pas d'asymptote, puisqu'on aurait prouvé que la fonction passe bel et bien par y=0.

Or, en regardant cette équation, on peut tout de suite constater qu'il n'y a aucune solution, car aucun exposant, peu importe quelle est la base, ne nous permet d'obtenir 0. En d'autres mots, 2 exposant quelque chose égal 0? C'est impossible.

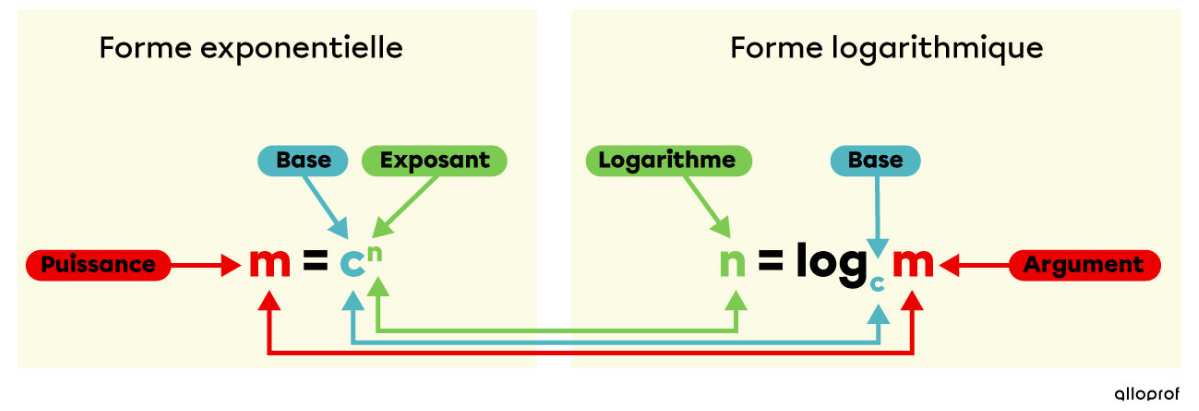
Poussons l'analyse plus loin. Admettons que nous n'avions pas remarqué cela et que nous essayions tout de même de résoudre l'équation. Il faudrait transformer la forme exponentielle en forme logarithmique :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce qui nous donne :

$$0=2^x$$

$$x=log_{2}0$$

Si on essaie ce calcul sur notre calculatrice, on constatera qu'il n'y a pas de résultat, pour la même raison mentionnée précédemment.

C'est la même chose pour la fonction \(g(x)=3\times 2^x+5\), il n'y a aucune valeur en x qui nous permet d'avoir y=5. Faisons le test :

$$5=3\times 2^x+5$$

$$5-5=3\times 2^x+5-5$$

$$0=3\times 2^x$$

$$\frac{0}{3}=\frac{3\times 2^x}{3}$$

$$0=\times 2^x$$

$$x=log_{2}0=∅$$

Voilà! J'espère que cela répond à tes questions! :)

Salut!

C'est une excellente question! En fait, le facteur 4 est là justement parce que notre variable x est le temps écoulé en heure.

Le paramètre b représente le nombre de fois que le facteur multiplicatif est appliqué dans une période donnée.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ainsi, puisque notre variable x est en heure et qu'il y a 4 tranches de 15 minutes en une période de 1 heure (la variable x), alors b=4.

Voici d'autres exemples pour t'aider à mieux comprendre comment déterminer le paramètre b :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Si notre variable x était le temps écoulé en minutes, alors b serait égal à 1/15, car l'événement se produit 1 fois aux 15 minutes.

On peut faire le test pour le vérifier :

$$N(x)=10(2)^{\frac{1}{15}x}$$

On cherche le nombre de bactéries après 5h, donc après 5×60=300 minutes :

$$N(x)=10(2)^{\frac{1}{15}300}=10485760$$

On obtient bel et bien le même résultat!

J'espère que c'est plus clair pour toi! :)

Salut!

Pour représenter graphiquement un système d'équations, tu dois placer dans le graphique chaque fonction représentée par les équations.

Par exemple, si on a ce système d'équations linéaires :

$$\left\{\begin{matrix} y_{1}=\frac{1}{2}x+3 \\y_{2}=-x-3 \end{matrix}\right. $$

On doit tracer dans le graphique la droite \(y_{1}=\frac{1}{2}x+3\) ainsi que la droite \(y_{2}=-x-3\). En résolvant le système, on va pouvoir trouver les coordonnées du point d'intersection des deux fonctions, c'est-à-dire les coordonnées du point où les deux droites se croiseront, où elles se toucheront :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici des fiches qui pourraient t'être utiles : 

• Tracer une fonction affine | Secondaire | Alloprof
• La résolution de systèmes d'équations linéaires | Secondaire | Alloprof

J'espère que c'est plus clair pour toi! :)