Best Of
Question
Bonjour,
Pourquoi, on ne peut pas crée notre nom.
Je ne parle pas de ex: PoissonBeta4951.
Je parle de ex: soccerbeta8976
Re: Question
Bonjour,
Dans ce cas, tu arrondis au nombre le plus près.
Voici un lien qui te sera utile. Il contient même un vidéo :
Bonne journée :)
Re: Question
Salut!
La liaison est une fonction mécanique qui permet à deux pièces d'un objet technique d'être liées ensemble.
Le guidage est une fonction mécanique élémentaire effectuée par un ou plusieurs organes d'un objet technique qui force une autre partie de l'objet technique à effectuer un certain mouvement.
Ainsi, la liaison lie deux morceaux, tandis que le guidage guide le mouvement de morceaux.
N'hésite pas à nous réécrire si tu as d'autres questions! 😁
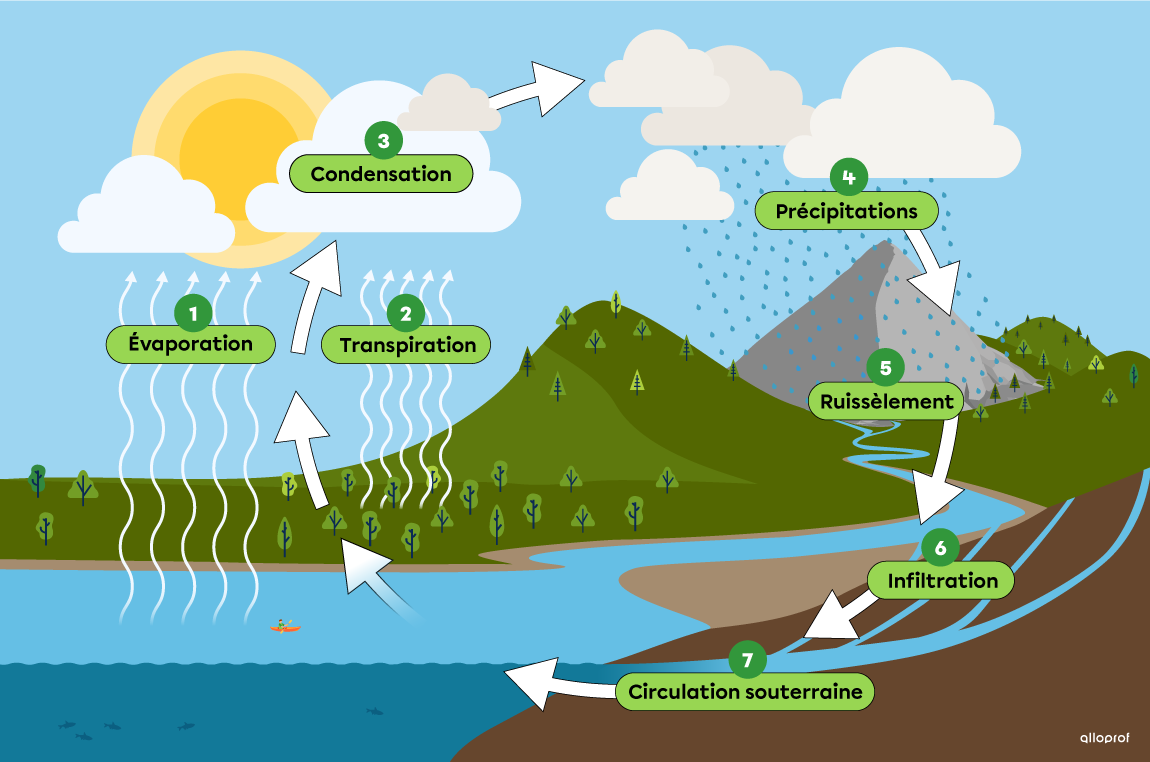
Re: Question
Salut!
Le cycle de l’eau est la circulation continuelle des molécules d’eau dans l’hydrosphère.
Je t'invite à consulter la fiche suivante : Le cycle de l'eau | Alloprof
Et à revenir nous voir si tu as d'autres questions! :)
Question
Je suis en secondaire 1 et je me demandais parce qu'on fait un projet en sciences d'un appareil photo type sténopé j'ai vu sur alloprof que c'est en secondaire 5 c'est normal?
Re: Question
Bonjour PommeAutonome7874,
Voici 2 vidéos qui peuvent vous aider à mieux comprendre la factorisation en espérant que ça vous aide
Re: Question
Salut!
Tu dois factoriser chaque partie séparément!
Prenons un exemple pour mieux comprendre :
$$ \frac{x^2-9}{x^2-x-6}$$
On a le numérateur \( x^2-9\) et le dénominateur \(x^2-x-6 \). On doit factoriser chacune de ces parties séparément.
Pour le numérateur, on peut utiliser la technique de la différence de carrés.
$$x^2-9=x^2-3^2=(x-3)(x+3)$$
Pour le dénominateur, on peut utiliser la technique du produit-somme.
$$x^2-x-6=(x-3)(x+2)$$
On remplace maintenant le numérateur et le dénominateur dans notre fraction initiale par les expressions factorisées.
$$ \frac{x^2-9}{x^2-x-6}$$
$$ \frac{(x-3)(x+3)}{(x-3)(x+2)}$$
Finalement, on simplifie les facteurs qui se retrouvent à la fois au numérateur et au dénominateur. Dans cet exemple, on peut simplifier (x-3) :
$$ \frac{(x+3)}{(x+2)}$$
$$ \frac{x+3}{x+2}$$
Voilà!
En résumé, tu dois simplifier chaque partie en utilisant l'une des techniques de factorisation.
Voici une fiche qui pourrait t'être utile :
J'espère que c'est plus clair pour toi! N'hésite pas à nous réécrire si tu as d'autres questions! 😁
PS Si tu as un exercice en particulier qui te pose problème, tu peux nous l'envoyer en photo, ça nous fera plaisir de t'aider!
Re: Question
Bonjour,
Merci pour ta question!
L'énergie d'ionisation représente l’énergie nécessaire pour arracher un électron à un atome. Cette valeur est différente pour chaque élément.
Voici une fiche pour plus d'informations :
Tu peux aussi consulter ce lien pour avoir une liste des énergies d'ionisation des éléments du tableau périodique :
N'hésite pas si tu as d'autres questions!
Zachary T. :)
Re: Question
Coucou
Merci d'utiliser la Zone d'entraide:)
Voici un petit résumé des types de triangle :
Triangle équilatéral
- Côtés : 3 égaux
- Angles : 3 égaux
Triangle isocèle
- Côtés : 2 égaux et 1 différent
- Angles : 2 égaux
Triangle scalène
- Côtés : 3 différents
- Angles : 3 différents
Triangle rectangle
- Côtés : N'importe
- Angles : 1 angle droit
Triangle aigu
- Côtés : N'importe
- Angles : Tous les angles sont aigus
Triangle obtus
- Côtés : N'importe
- Angles : 1 angle obtus
N'hésite pas de poser d'autres questions:)
RubisFiable7243
Re: Question
Les triangles se classent en fonction de la longueur de leurs côtés ou de la mesure de leurs angles. Les principaux types sont le triangle scalène (trois côtés de longueurs différentes), l'triangle isocèle (deux côtés de même longueur), et le triangle équilatéral (trois côtés de même longueur). On peut aussi les classer selon leurs angles, en les qualifiant de triangle rectangle