Best Of
Re: Question
Salut !
Prenons la première ligne comme exemple. S'agit-il d'une incertitude relative de 10,11 %. Si c'est le cas, l'écriture est incorrecte, car lorsque le symbole \(\pm\), il te faut utiliser l'incertitude absolue.
Elle se calcule en multipliant l'incertitude relative à la valeur obtenue. Sinon, je te conseille quand même de visiter la fiche ci-haut pour plus de détails.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut!
Je t'invite à consulter la fiche suivante :
Et à revenir nous voir si tu as d'autres questions! :)
Re: Question
Salut LunePacifique3627 !
Merci d’utiliser la Zone d’entraide ! Je vais pouvoir t’aider.
Pour commencer, pour calculer la concentration il faut d’abord savoir ce que c’est : La concentration est la quantité de masse de soluté par rapport à la quantité totale de la solution. La formule est donc c = m/v. La concentration peut être demandée en g/L ou % m/v ( ou m/m, v/v car le m signifie “masse” et v signifie “volume”, ses abréviations sont utilisées pour dire si c'est une solide dans un liquide, un solide dans un solide et ect…), la différence est que la concentration sera en rapport avec 1L pour g/L et pour % m/v la concentration sera en rapport pourcentage (100%). Pour le calcul de c en g/L tu peux simplement diviser m par v (fait attention car si tu fait ça tu dois avoir le v convertit en L) et pour en % m/v la même chose mais multiplié par 100%. Il est aussi possible d’utiliser le produit croisé comme ceci :
g/L
2g/50ml = c/1L ( c est la variable cherché )
% m/v
2g/50ml = c/100%
Si par exemple tu connais c et v mais tu cherche m tu peux isoler la variable comme en math.
Ensuite pour la dilution, la dilution est le procédé de réduire la concentration en ajoutant du solvant. Il est important de savoir que tu n'auras aucunement besoin de faire attention à la masse puisque qu’elle sera la même avant et après. La formule est C1 x V1 = C2 x V2. Donc dans une situation ou tu dois trouver la concentration finale voici ce que tu dois faire:
Ex.
C1 = 9% m/v C1xV1 = C2xV2
V1 = 50ml Isole la variable C2
C2 = ? C1xV1 / V2 = C2
V2 = 450ml ensuite fait le calcul.
(écrire les informations connus sur le coté est très utile.)
Tu as aussi demandé à propos de la solution mais celle-ci n'a pas de calcul, une solution c’est un mélange homogène qui a une solvant et un soluté.
Voici quelques fiches pour t’aider:
https://www.alloprof.qc.ca/fr/eleves/bv/sciences/la-concentration-s1035
https://www.alloprof.qc.ca/fr/eleves/bv/sciences/la-concentration-et-ses-unites-de-mesure-s1028
J'espère que j’ai pu t'aider, n'hésite pas à poser des questions de nouveau dans la Zone d’Entraide et merci de ta confiance, nous sommes toujours là pour t’aider !
Bon courage, ne lâche pas !
RobotArtistique9041
Re: Question
Salut!
la forme générale est :
f(x) = 0,2x^2 + 2x + 6
∆ = -0,8
- Tu as oublié de multiplier le 0,2 aux termes 10x et 25.
Bonne soirée :)
Re: Question
Salut !
N'hésite pas à effectuer ta démarche sans sauter d'étape. Commençons par développer la parenthèse.
$$ f(x)=0,2(x+5)^2+1 $$
$$ 0=0,2(x^2+10x+25)+1 $$
$$ 0=0,2x^2+2x+25 $$
Tu peux essayer avec cette équation plutôt.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut !
Il n'est pas évident de vérifier toutes les valeurs, mais lorsqu'il est question d'aire latérale, il faut d'abord calculer la circonférence du cylindre, puis calculer l'aire latérale à l'aide de la hauteur.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut !
La moyenne pondérée est utilisée quand les données n'ont pas toutes la même importance. Dans ce cas, on donne un poids (généralement en pourcentage) à chacune des valeurs.
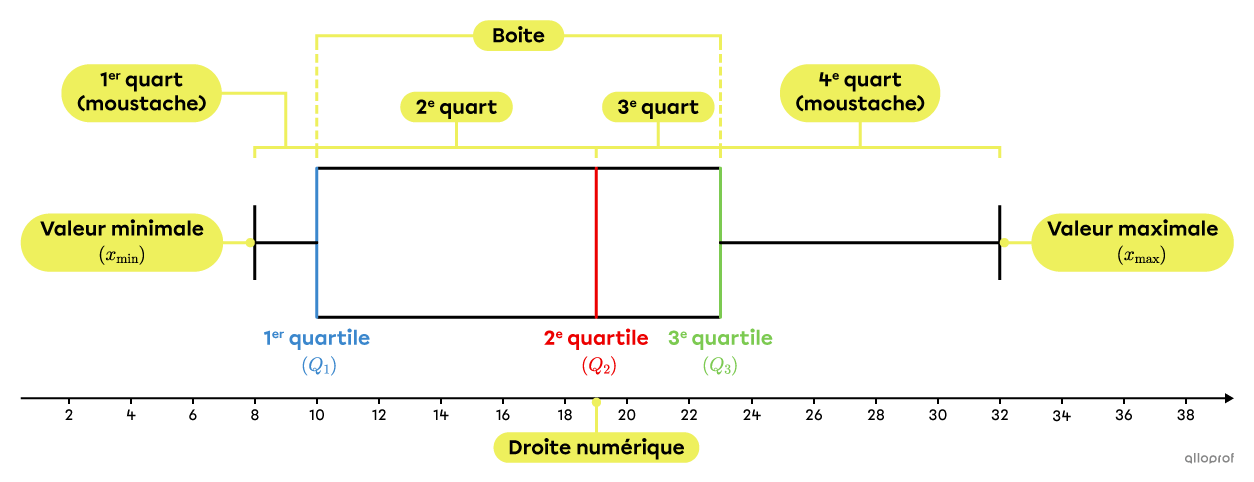
L'exemple le plus commun est la pondération des examens (voir fiche ci-haut). L’étendue interquartile, notée EI, correspond à l’étendue entre le 1er quartile (Q1) et le 3e quartile (Q3).
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut !
Il est difficile de simplifier un phénomène complexe. Le mieux est d'y aller étape par étape. Le rôle du système respiratoire est d’approvisionner l’organisme en dioxygène (O\(_2\)) et d’en expulser le dioxyde de carbone (CO\(_2\)).
Tu peux voir dans le schéma que l'oxygène entre dans le système sanguin et du CO\(_2\) est expulsé. Mais pour être précis, l'air inspiré est riche en oxygène et l'air expiré est moins riche en oxygène.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Bonjour!
Premièrement, d'après de ce que j'ai compris, tu parles probablement de la loi du service naval. Dans ce contexte, la "marine" désigne la flotte de bateaux de guerre d'un pays. Donc, étant encore une dominion, la marine canadienne aiderait à consolider l'Empire britannique, car elle aurait plus de puissance millitaire. J'espère que j'ai pu t'aider. Bonne journée!
Re: Question
Salut!
Cela dépend essentiellement du problème spécifique.
- Par définition, le périmètre d'une figure plane est la somme de ses côtés. Est-ce qu'on t'a donné des indices pour trouver les mesures des côtés?
- Il est également possible que tu dois trouver le périmètre en établissant une équation où le périmètre est le seul inconnu.
Bref, c'est tout ce que je peux trouver pour le moment sans voir la question.
Bonne journée :)