Secondary V • 1yr.
Bonjour!
Je suis en train d'apprendre les lois des logarithmes. J'avais une confusion par rapport à un loi.
La-voici:
En fait, dans l'écriture de cette loi, je n'arrive pas à comprendre où est-ce que se trouve la base et quelle est sa valeur? Pour la première partie, je comprends que c'est log de a à la base de c, mais dans la côté droite de l'égalité, si j'écris log de a ou bien log de c, c'est à la base de quoi?
Merci pour la clarification :D
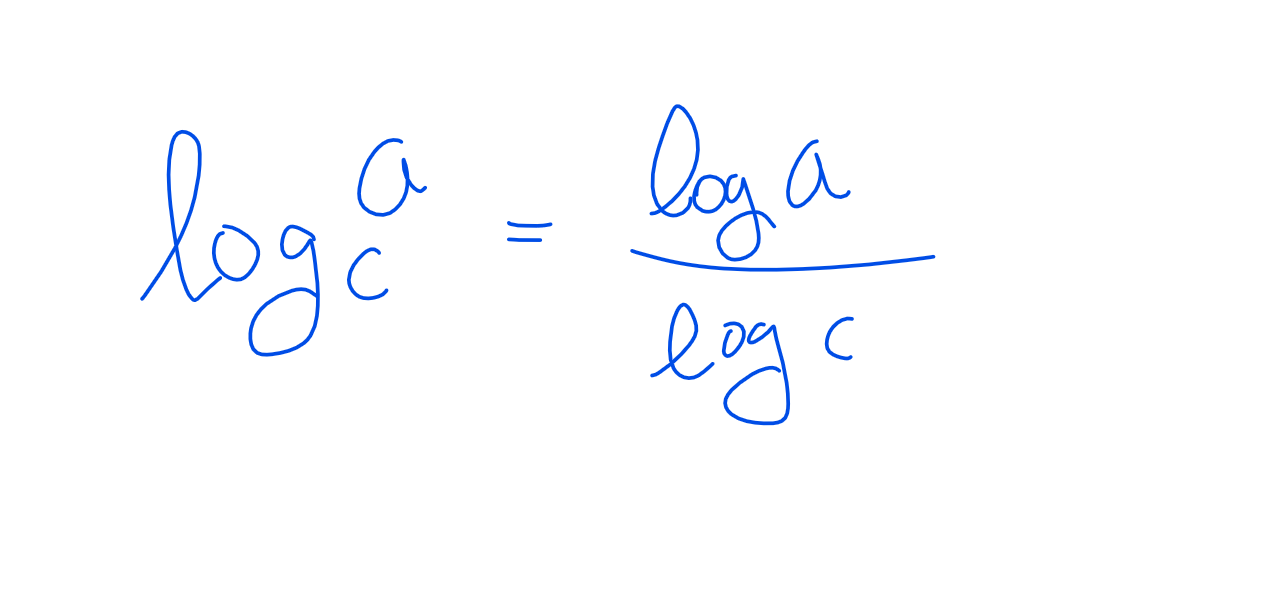
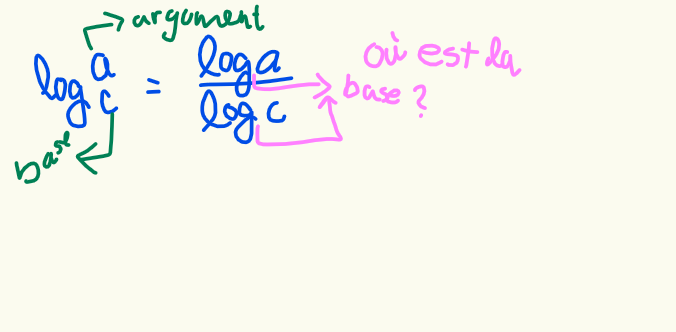






Je suis d'accord avec toi. Ce n'est pas si clair.
Par convention quand la base n'est pas spécifiée "le log" est "le log en base 10".
Par ailleurs si on utilise "ln" c'est le log en base e où e = 2.718.. on l'appelle le logarithme naturel (parce que ln(e) = 1) ou népérien en l'honneur du mathématicien écossais John Neper qui établit les premières tables logarithmiques.
Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Salut!
La base peut être n'importe quel chiffre, tant qu'elle est identique au logarithme du numérateur et à celui du dénominateur!
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Voici un exemple :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
On a choisi de mettre 10 comme base au logarithme, mais on aurait aussi pu prendre un autre nombre, 2 par exemple :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Le résultat aurait été le même!
On choisit habituellement la base 10, car le bouton log sur nos calculatrices est en base 10. De plus, si la base n'est pas explicitement écrite, cela signifie qu'elle est de 10 :
$$log5=log_{10}5$$
J'espère que c'est plus clair pour toi! :)