J'ai ce problème à résoudre. Je suis capable d'en faire une partie, mais j'aurais besoin d'aide pour le terminer. Voici ce que j'ai fait:
1- J'ai trouvé la distance entre le point A et le point B, soit 500 mètres.
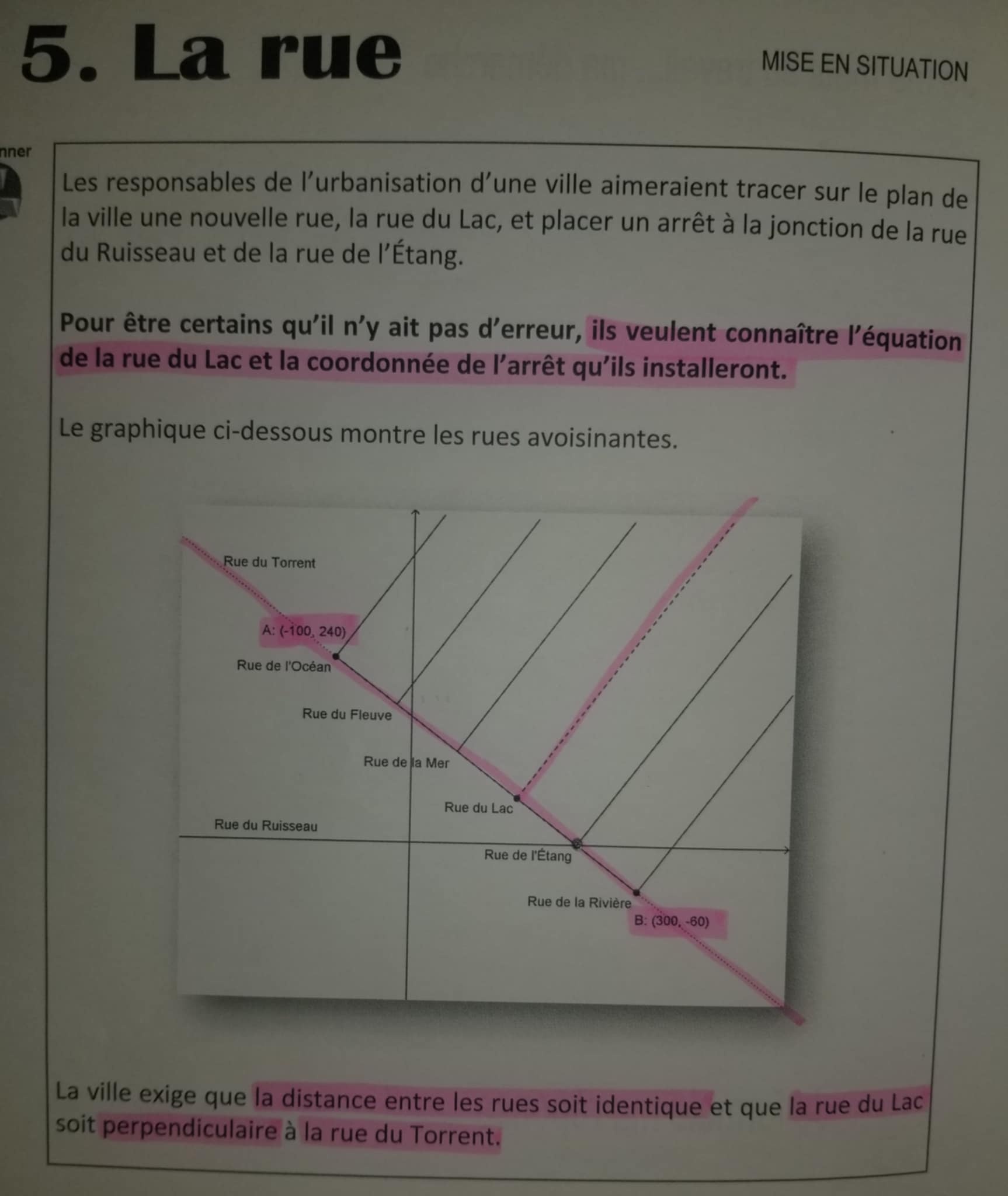
2- J'ai calculé la pente de la rue du Torrent. Cela m'a donné -3/4. Donc, la pente de la rue du Lac est son opposé, puisque ces deux rues sont perpendiculaires. Cela donne environ 1,33.
3- Ensuite, j'ai trouvé l'équation de la rue Torrent: y = -0,75x + 165. Avec cette équation, j'ai trouvé les coordonnée de l'arrêt de la rue de l'Étang, soit 220, 0). Le point arrive sur le 0 pour le y sur le graphique. Et donc, j'ai remplacé le y dans l'équation par 0, ce qui m'a donné 220 pour le x.
4- Je suis rendue à trouver l'équation de la rue du Lac, mais je ne vois pas comment y arriver.






Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Salut !
Je te félicite d'avoir compléter la majorité de l'exercice par toi-même ! Pour le reste tu peux trouver le point de croisement entre la rue du Lac et la rue du Torrent.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Tu peux la distance (en \(y\) et en \(x\)) entre les rues est la même, tu peux donc trouver la position relative entre croisement et donc les coordonnées du point de croisement avec la rue du Lac. Puis avec ce point et la pente de la rue du Lac, tu peux calculer la règle de sa fonction.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !