Bonsoir!
En tentant de résoudre l'équation valeur absolue suivante, j'ai eu une erreur. Pourtant, je n'arrive pas à saisir l'erreur dans mon raisonnement:
En fait, si je ne me trompe pas, l'un des principes de bases qu'on avait appris était que, lorsque j'ai un produit dans une équation (côté gauche de l'égalité), chaque portion du produit équivaut à l'équivalence (côté droite de l'égalité). Par exemple:
x(2x+1)=4
1- x = 4
2- 2x+1 = 4
J'ai utilisé ce même principe pour ce problème, mais cela ne fonctionne pas. Y a-t-il un détail qui me saute à l'oeil? Ou encore, une méthodologie plus approprié pour résoudre cette équation?? Si oui, pouvez-vous s'il-vous-plaît me guider à travers la résolution? J'éprouve vraiment de la difficulté!
J'apprécierais sincèrement toute résolution avec explications détaillées. Merci pour votre aide :)
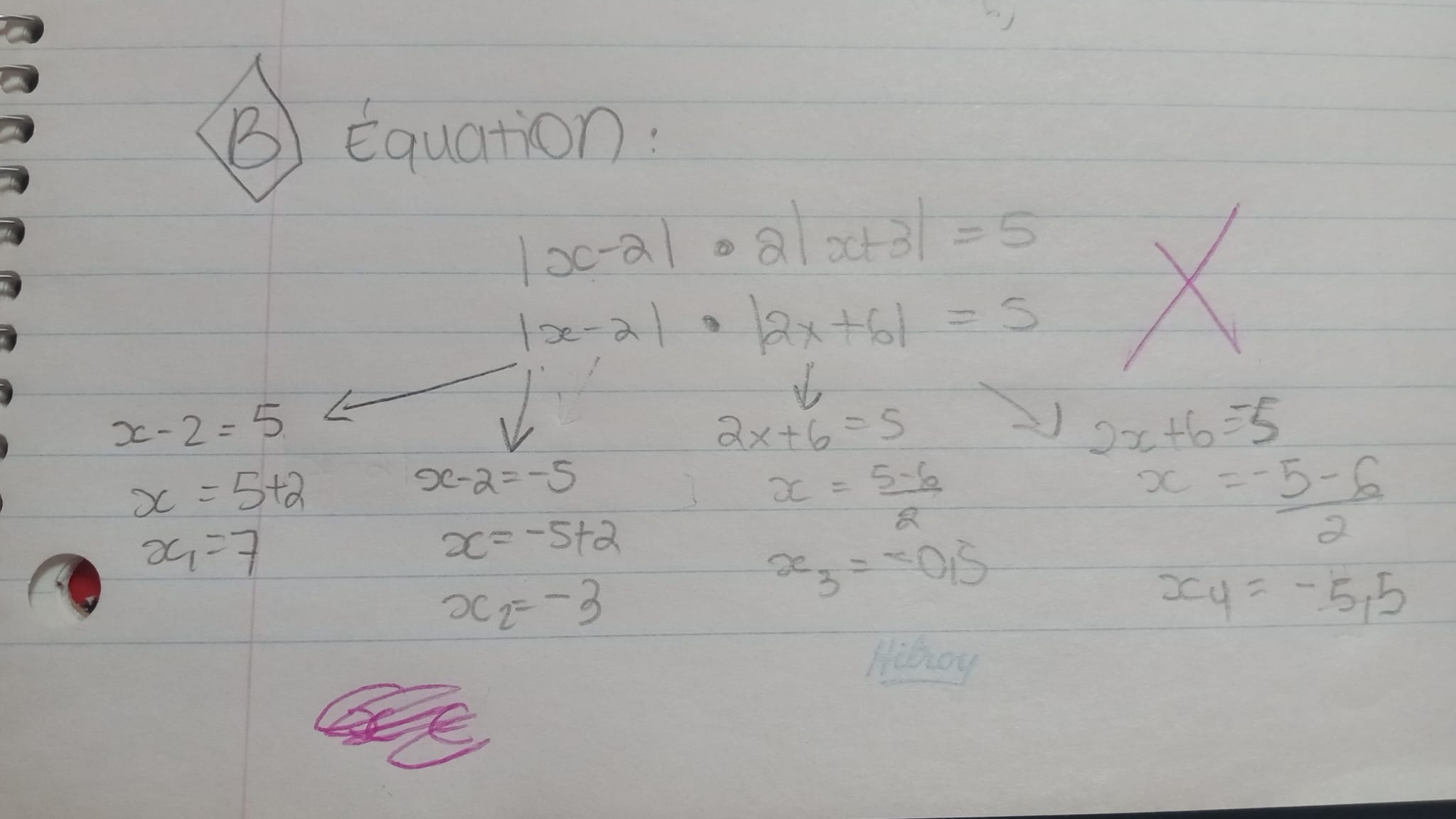






Une autre façon de résoudre le problème serait de diviser le problème initial en deux :
1- ou bien 2(x-2)(x+3)=5
2- ou bien 2(x-2)(x+3)=-5
En effet, si le produit donne -5 les valeurs absolues rendront le produit positif.
Tu devrais obtenir 4 réponses puisque chacune des deux possibilités donne deux réponses puisque ce sont des équations du deuxième degré.
Bonjour PistacheRose369,
Ce problème est complexe mais il se fait...
Tout d'abord, j'attire ton attention sur ton point de départ : «lorsque j'ai un produit dans une équation (côté gauche de l'égalité), chaque portion du produit équivaut à l'équivalence (côté droite de l'égalité)». Tu ne peux utiliser cette façon de faire que lorsque le côté droit est égal à zéro. C'est très important.
Si je reprends ton exemple, tu peux facilement vérifier que x=4 n'est pas une solution au problème initial : 4(2*4+1) n'est pas égal à 4.
On ne peut donc pas commencer le problème de la façon que tu suggères. Il va falloir travailler fort...
Si x≥2, alors on sait que l'argument des deux fonctions valeur absolue est positif. On peut alors se débarrasser des valeurs absolues. On obtient alors 2(x-2)(x+3)=5, ce qui est une fonction du deuxième degré que tu peux résoudre. Tu obtiendras probablement 2 réponses que tu devras tester.
Si x est entre -3 et 2, alors l'argument de la première fonction valeur absolue est négatif donc la valeur absolue fait changer le signe (mais l'autre argument demeure positif). On peut alors écrire 2(-x+2)(x+3)=5. Même stratégie : on résout et on teste les 2 réponses.
Il reste le cas où x est inférieur à -3. Les deux arguments sont alors négatifs, les deux valeurs absolues changent les signes et on doit résoudre 2(-x+2)(-x-3)=5. Il faut encore tester les solutions.
C'est long, mais ça se fait...
Explanation verified by Alloprof
This Explanation was verified by a member of the Alloprof team.
Tu ne peux faire cela!!
x(2x+1)=4
1- x = 4
2- 2x+1 = 4
en 1- x = 4/(2x+1) et en 2- 2x+1 = 4/x
c'est seulement si x(2x + 1) = 0
que tu as ou bien
x = 0
ou bien
2x + 1 = 0
Pour ton équation
|x-2|·2|x+3|=5
tu dois envisager toutes les possibilités pour les valeurs absolues et résoudre l'équation résultante dans chaque cas:
• si x>2 alors |x-2| est la valeur absolue d'un nombre positif donc |x-2| = x-2 et aussi |x+3| = x+3
ce qui donne 2(x-2)(x+3) = 5
2(x²+x-6) = 5 => 2x²+2x-17 = 0 à résoudre
• si -3<x<2 alors |x-2| est la valeur absolue d'un nombre négatif donc |x-2| = -(x-2) et |x+3| = x+3
• si x <-3 alors |x-2| = -(x-2) et |x+3| = -(x+3)
• x ne peut être égal à 2 ou -3 car on aurait 0 = 5