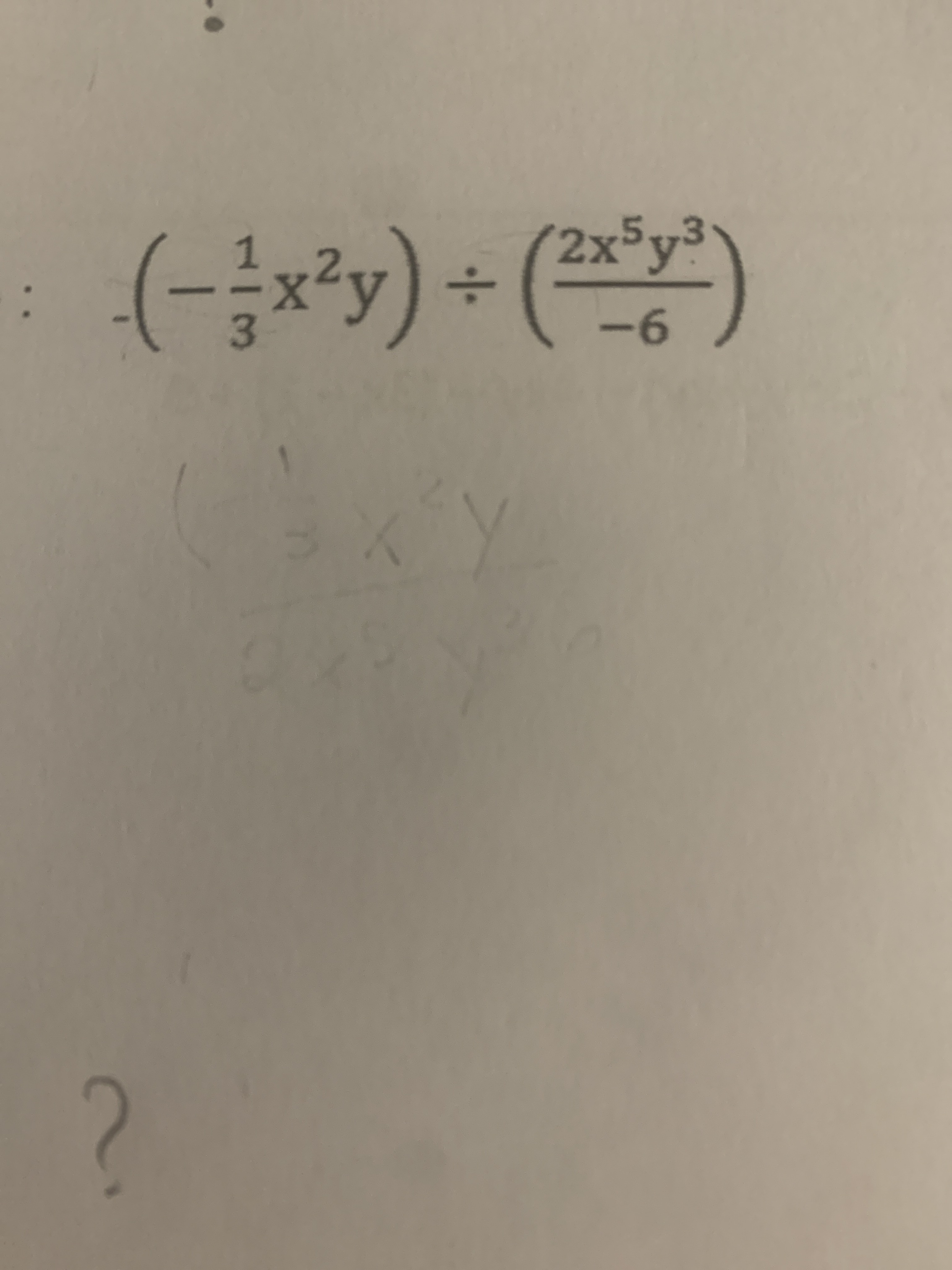
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
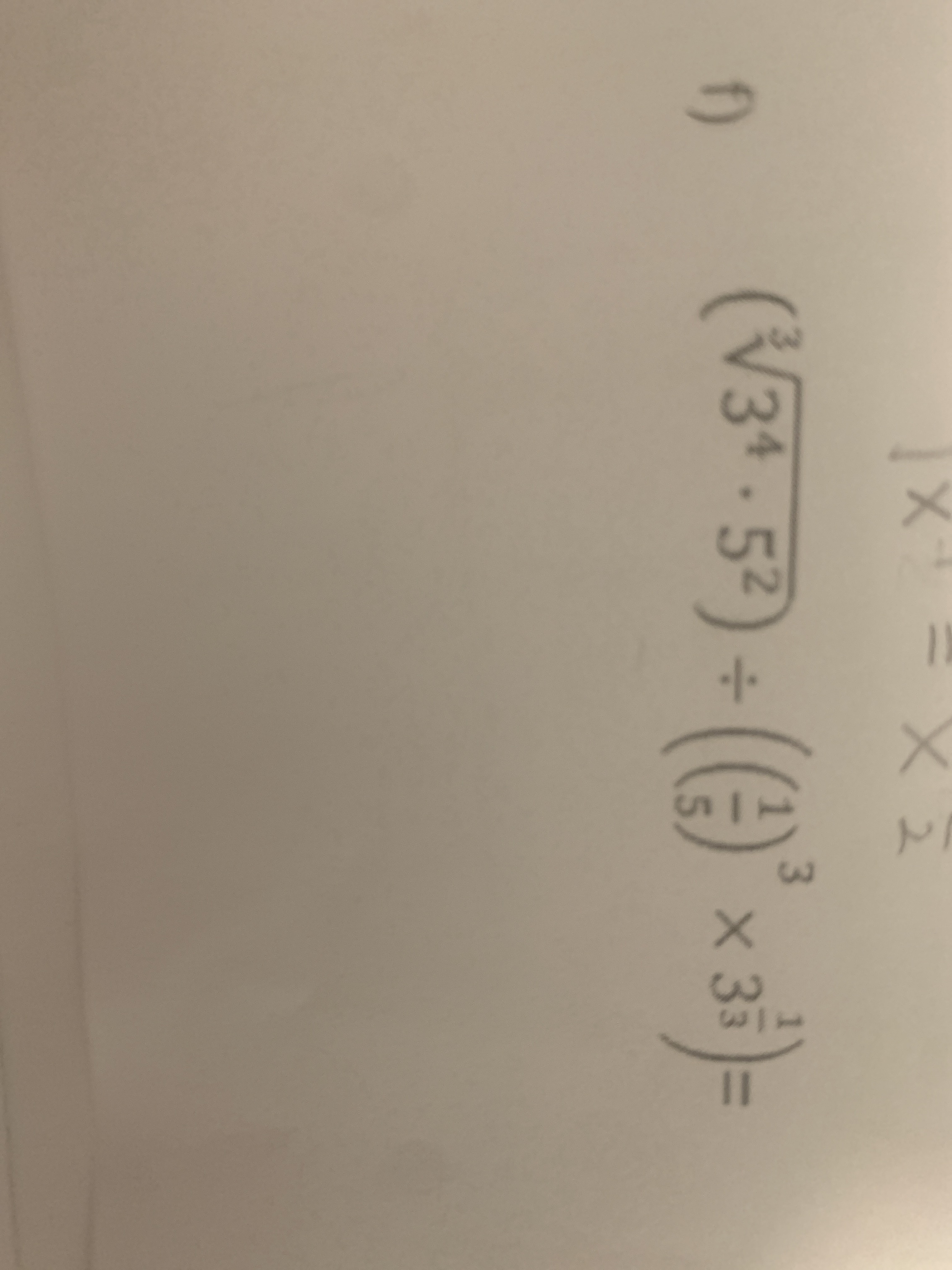
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
je ne sais pas par où commencer. Besoin d’aide 😥
Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Bonsoir, MandarineTranquille8232!
Tu as raison qu'une division vaut la multiplication de l'inverse.
Il ne faut toutefois pas laisser une fraction au numérateur. Tu peux mettre le 3 du premier terme au dénominateur de tout le terme.
De plus, tu as laissé le 6 du deuxième terme au dénominateur alors qu'il fallait l'inverser aussi. Pour éviter de telles erreurs, tu aurais pu simplifier 2/6 dès le début.
$$ -\left(-\frac{1}{3}x^2y\right)\div\left(\frac{2x^5y^3}{-6}\right) $$
$$ =-\left(-\frac{1x^2y}{3}\right)\times\left(\frac{-6}{2x^5y^3}\right)$$
$$ =--\frac{1x^2y}{3}\times\frac{-6}{2x^5y^3}\\ $$
Poursuis la démarche en appliquant la règle du quotient de puissances de mêmes bases:
Lorsque des notations exponentielles de même base sont divisées ensemble, on soustrait les exposants.
$$ \frac{a^{m}}{a^{n}}=a^{m-n}\ \text{où} \ a\neq 0 $$
Pour le deuxième exercice, tu dois utiliser d'autres lois des exposants.
Une base affectée d'un exposant fractionnaire se traduit en une racine.
$$ a^{\frac{m}{n}}=\sqrt [n]{a^{m}} $$
Puissance d'un quotient : On peut distribuer un exposant lorsqu'il affecte une parenthèse qui contient une division.
$$ \left( \frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}} \ \text{où} \ b\neq 0 $$
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/les-lois-des-exposants-m1044
N'hésite pas à poser d'autres questions!
Salut! Tkt jpeut t’aider pour le premier j’ai fait une démarche claire pi avec des étapes, le truc c!est de simplifier et de y aller étapes par étapes.Si ta d’autre questions (ou que je fait une erreur dit le moi!)J’espère que ça va bien t’aider!
Voila ma démarche:
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.