Secondary V • 2yr.
Bonjour AllôProf,
J'ai trouvé que la restriction de l'inéquation suivante était que x est plus grand ou égal à 0. Pourtant, le corrigé me dit que c'est la réponse alors que j'ai trouvé que x = -4 (x > -4) . Pouvez-vous m'aider à trouver ma faute svp? Merci :D
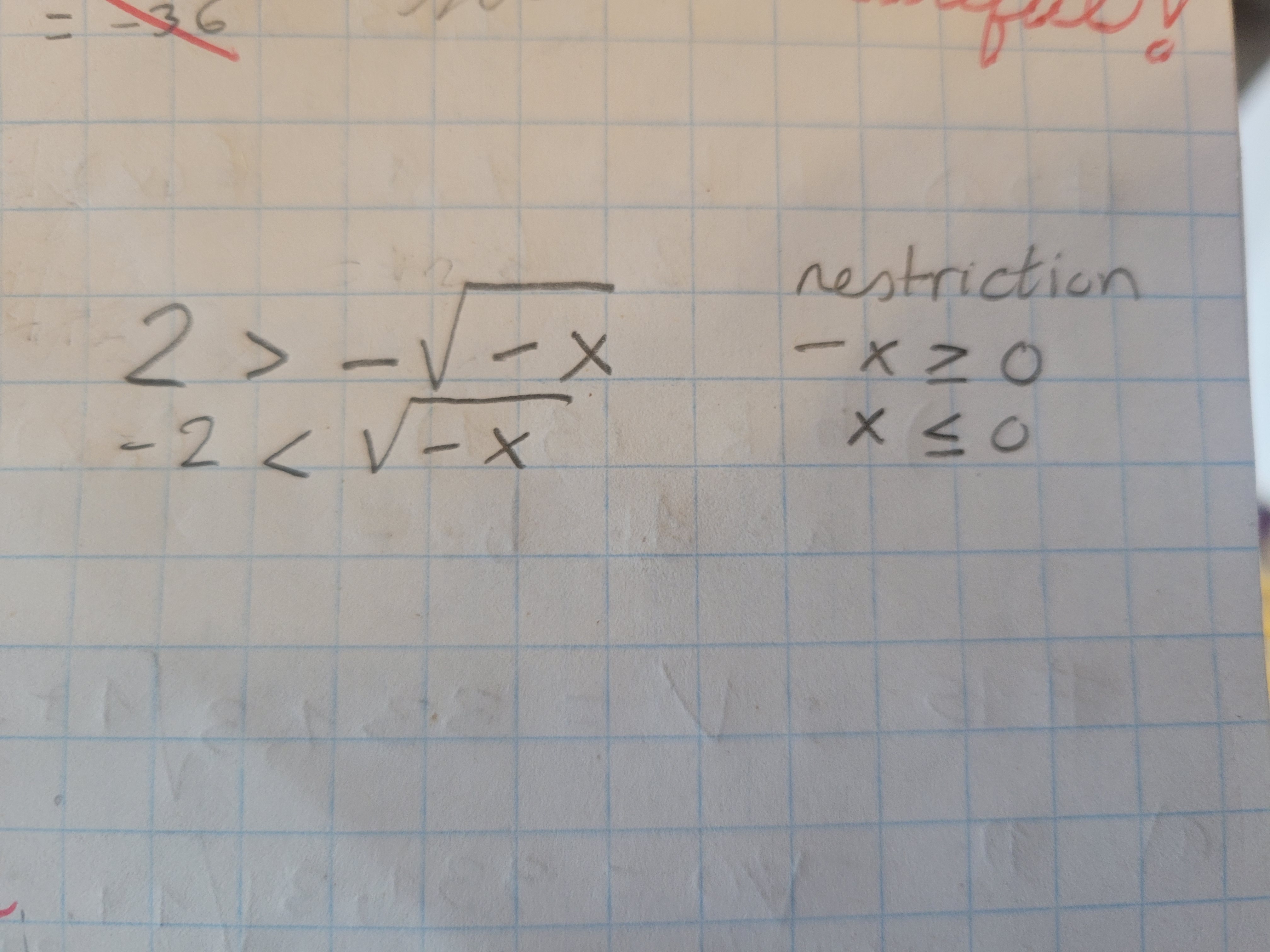






@zinc
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
?
6 > -5 vrai
6² > (-5)² vrai aussi
@@@
Remarque au sujet de √(-x) > -2 .
La plus petite valeur de √(-x) est 0.
Par conséquent √(-x) > -2 est toujours vrai lorsque défini.
@Kevin H
Or, la restriction x <=0 englobe la restriction x <-4 (car tout ce qui est en bas de -4 est aussi en bas de 0)
c'est plutôt le contraire la restriction x <-4 est plus restrictive que x <=0 donc on prend x <-4 .
tu a un Et entre ( x <=0 et x <-4 ), c'est une intersection des deux ensembles, dans le cours de logique mathématique le Et symbolise l'intersection des ensembles le Ou symbolise l'union .
Or tu viens de faire une union.
l'inéquation
2 > -Racine(-x)
la restriction est -x >=0 donc x < =0
l'inéquation
-2 < Racine (-x) est la même que la précédente
il y a eu juste une multiplication par -1 et inversion de l'inégalité
tu te retrouves avec une seule inéquation
2 > -Racine(-x) comme -Racine(-x) est toujours négatif
on a l'inéquation 2 > a un nombre négatif
est toujours vraie pour tout x du domaine de définition.
L'ensemble des solutions est :
x appartient a ]-l'infini, 0]
et vérifies n'importe quel nombre il vérifie l'inéquation.
Ton erreur
on n'élevés pas au carre dans cette situation
paracerque les nombres ne sont pas de même signe
2 > -5 mais c'est pas vraie que 2² > (-5)²
ca revient a 4 > 25.
Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Bonjour,
Je vais faire la première avec toi :
On a une première restriction : x <= 0 (pour qu 'il n y ai pas de négatif dans la racine) Deplus, l'équation est satisfaite pour tout x <=0 à cause du moins devant la racine.
Puis,
2> -sqrt(-x)
-2 < sqrt(-x)
4 <-x
x <-4
Or, la restriction x <=0 englobe la restriction x <-4 (car tout ce qui est en bas de -4 est aussi en bas de 0)
Donc, on va prendre la restriction la plus général qui satisfait l'équation soit x <=0.
Je te laisse poursuivre.
Bonne journée