Secondary IV • 2yr.
Bonjour, j'ai une grande expressions rationnel à factoriser avec multiplication et j'ai de la difficulté à factoriser après la multiplication.
Alors le problème est dans l'image où j'ai réussi à le multiplier
En suite j'ai essayer la mise en évidence simple au numérateur, mais ça ma donner...
x^4(x-7)+x^2(-32x+175)+(175x-1176)
Je ne peux pas factoriser cela avec mon numérateur. Peut-être que je ne dois pas rassembler mes termes semblable avant la factorisation?
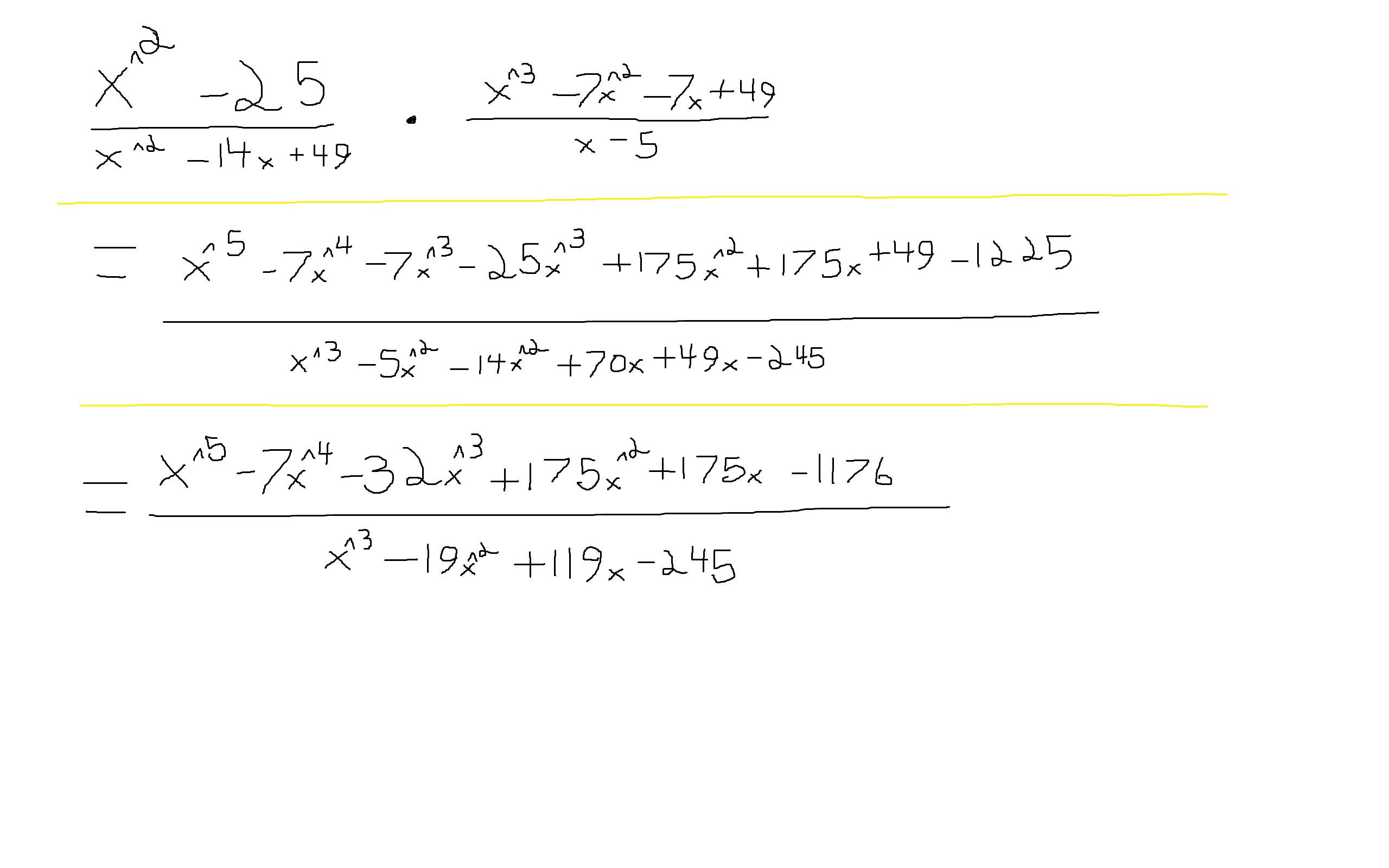






Quand on te demande de factoriser une expression ne commences jamais par multiplier, tu t'en sortiras jamais, il faut essayer de factoriser chaque terme de l'expression à part.
Exemple on commences par x²-25
25=5² on a donc x²-25= x²-5²
ca ressemble a l'identité a²-b²=(a+b)(a-b)
x²-25=(x+5)(x-5)
le deuxième polynôme
x²-14x+49 tu ne vois rien de spécial 49=7²
x²-14x+7² ca ressemble a un a²-2ab+b²=(a-b)²
effectivement 14=2 7
x²-14x+7²=x²-2 7x+7²
x²-14x+7²=x²-2 x 7+7²
x²-14x+7²=(x-7)²
Troisième polynôme
x³-7x²-7x+49 mais 49=7²
x³-7x²-7x+49 =x³-7x²-7x+7² il y a des 7 et des x partout
x³-7x²-7x+49 =x³-7x²-7x+7²
x³-7x²-7x+49 =(x³-7x²)-(7x-7²)
x³-7x²-7x+49 =x²(x-7)-7(x-7)
x³-7x²-7x+49 =(x-7)(x²-7)
on peut aussi factoriser x²-7 comme différence de deux carres, sachant que 7=(racine(7))²
(x²-7)=(x²-(racine(7))²)
(x²-7)=(x+(racine(7))(x-(racine(7)) mais c'est pas important dans notre cas paracerque ca ne va pas se simplifier.
On revient a l'expression de départ
(x²-25/x²-14x+49 )((x³-7x²-7x+49)/(x-5)) =
(x+5)(x-5)(x-7)(x²-7)/(x-7)²(x-5)
il y a du x-5 et du x-7 dans le dénominateur et le numérateur on simplifie.
(x+5)(x-5)(x-7)(x²-7)/(x-7)²(x-5)= on simplifie (x-5)
(x+5)(x-7)(x²-7)/(x-7)²= on simplifie (x-7)
(x+5)(x²-7)/(x-7)
Résultat final
(x²-25/x²-14x+49 )((x³-7x²-7x+49)/(x-5)) =(x+5)(x²-7)/(x-7)
Explanation verified by Alloprof
This Explanation was verified by a member of the Alloprof team.
Il est préférable de factoriser avant de multiplier pour ne pas compliquer le problème.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.