Bonsoir,
J'aimerais savoir comment évaluer la somme qui suit à l'aide des formules ainsi que des théorèmes de la sommation.
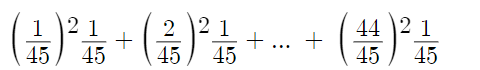
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Voici ma démarche :
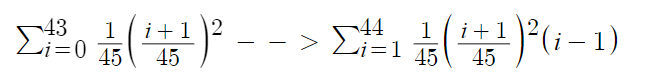
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
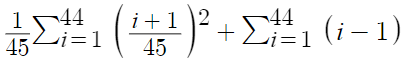
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ensuite, étant donné qu'il est question de la sommation de i^2, je me suis dit que je devrais faire 1/45 (k(k+1)(2k+1)/6)).
Merci et bonne soirée! ;)
OrAutonome2754
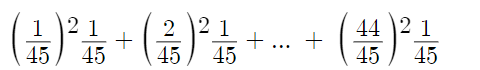
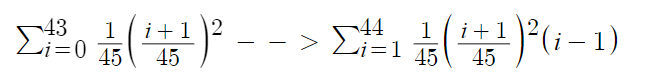
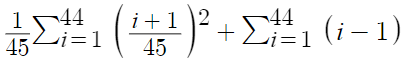






Explanation verified by Alloprof
This Explanation was verified by a member of the Alloprof team.
tu dois sortir 1/45 de la formule, puis tu as chaque terme de la forme (i/45)² de 1 a 44
puis le (i/45)²=i²/45²
le 1/45² est partout le même, sors le de la somme
tu auras S=1/45³(1+2²+3²+........+42²+43²+44²)
c'est la somme des carres tu a la formule du cours
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
(1+2²+3²+........+(n-1)²+n²) =n(n+1)(2n+1)/6
S=(1/45³)(44(44+1)(2*44+1)/6
S=(1/45³)*44*45*97/6
S=(1/45²)*44*97/6