Postsecondary • 2yr.
Salut!
J'ai une question par rapport à un exercice de dérivation implicite en calcul différentiel.
L'exercice demande de trouver la dérivée de xe^y=y*sin(x).
Je me demande juste pourquoi dans la partie de droite, la dérivée de y*sin(x) donne : y'sin(x)+ycos(x). De mon côté, en le faisant, j'obtenais y*y'*sin(x)+y*cos(x), donc j'avais un y de plus. Je l'ai mis parce que normalement, la dérivée de y, c'est y*y', non?
(J'ai joint ma démarche)
Merci!
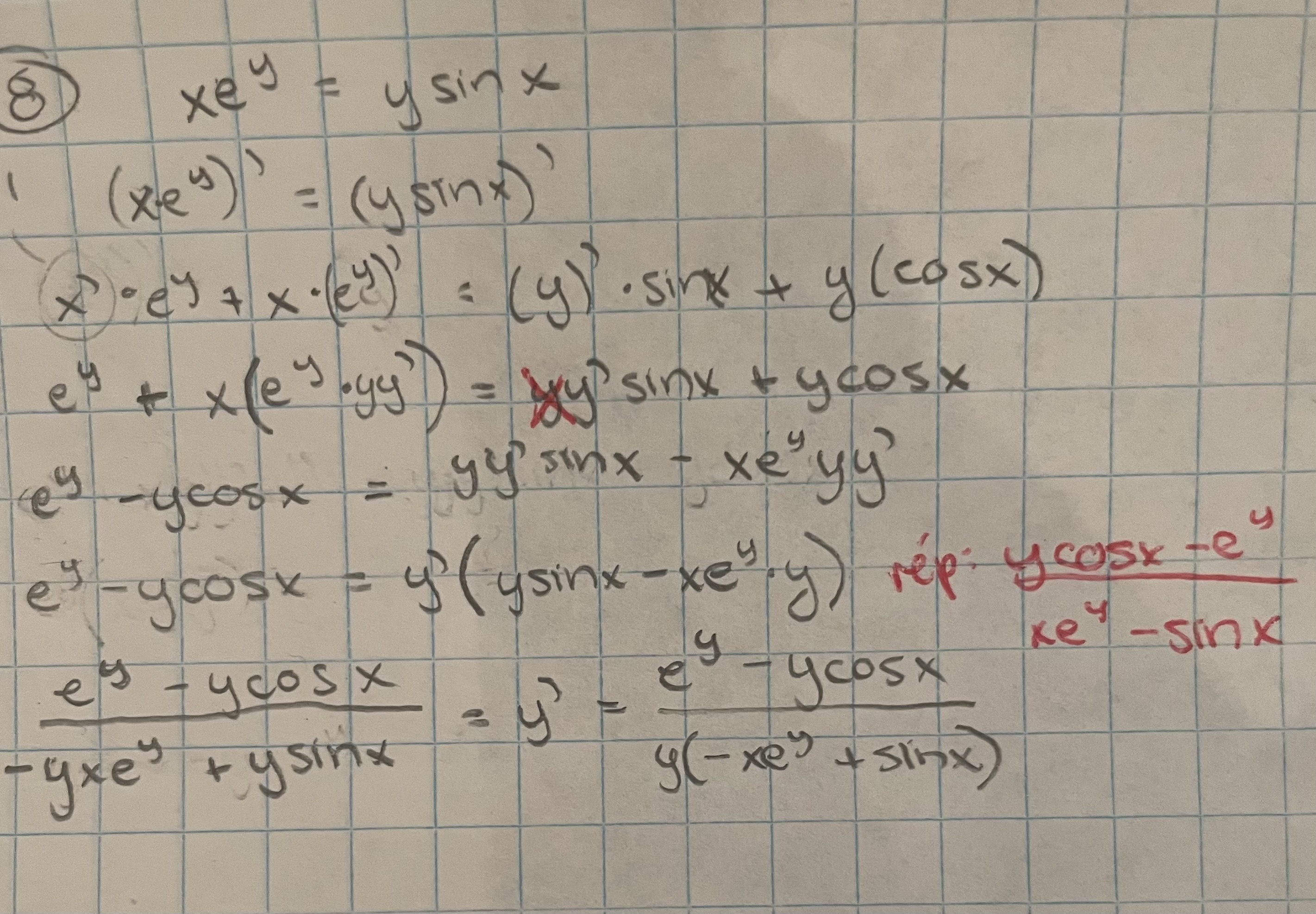






☺
On a y=f(x) alors la dérivée de y peut s'écrire y' ou f'(x), mais pas yy' ni f(x)f'(x).
Explanation verified by Alloprof
This Explanation was verified by a member of the Alloprof team.
La dérivée de y par rapport à x que (y' ou dy/dx): c'est ce que tu cherches
J'ai corrigé tes erreurs, tu as besoin de revoir les règles de dérivation.
https://w1.cirrelt.ca/~errico/table_derivees.pdf
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.