Help Zone

Salut !

Commençons par #5. Dans le a), ton erreur provient du découpage de la figure. Voici une des possibilités.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ainsi, il vaut mieux y aller étape par étape. Pour le carrée orange, tu dois multiplier (x+3) avec la base. Cette base peut être trouvé en soustrayant (3x+2) à (5x). Pour le carrée, l'un des côté est 5x, mais l'autre doit être calculé en soustrayant (x+3) à (4x+1).

Pour le b), tu dois commencer par trouver la valeur de x en résolvant :

$$ x+3=5\rightarrow x=2 $$

Puis, tu remplaces x dans ton expression en a).

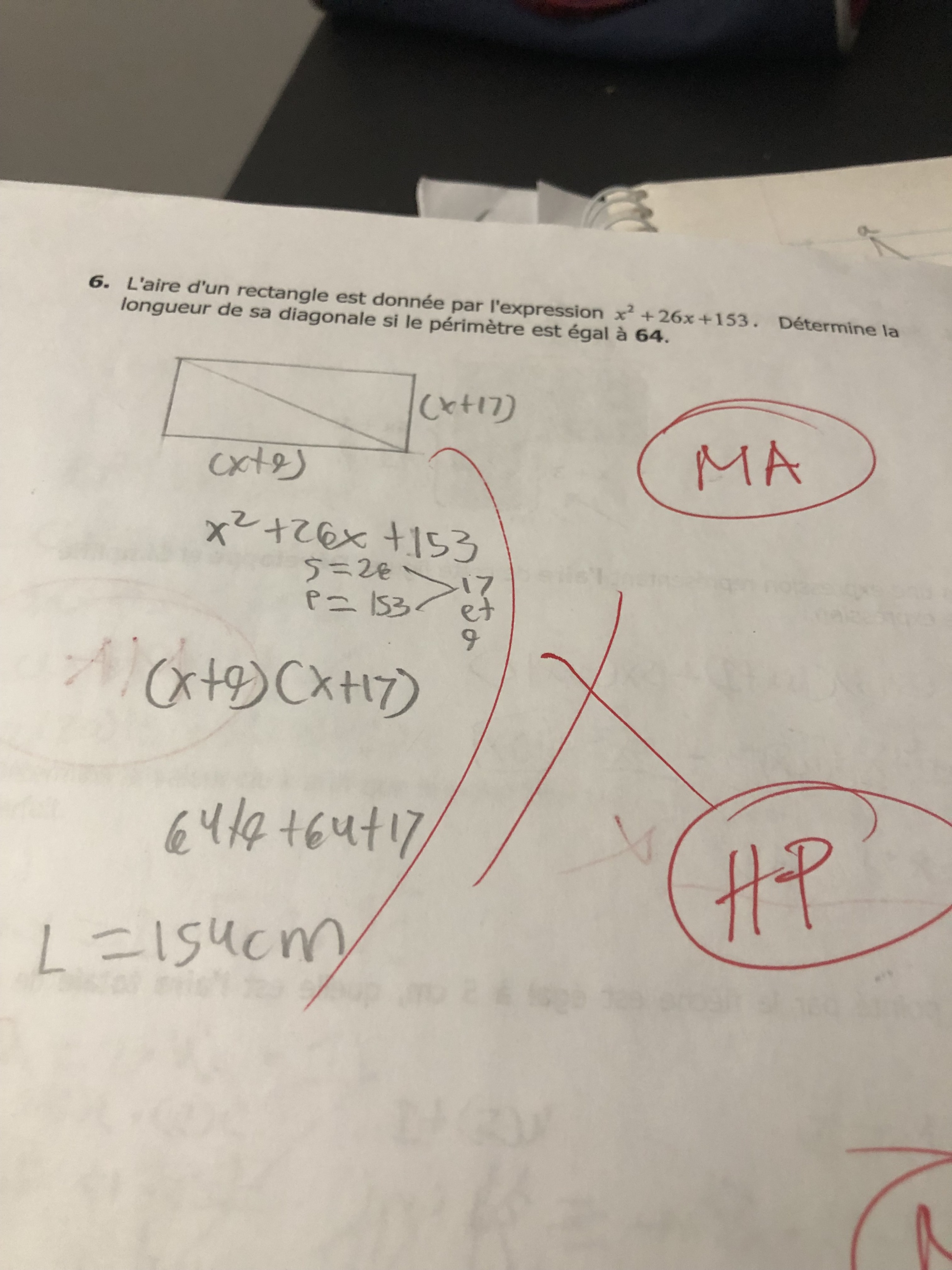
Pour le #6, tu as bien factorisé même si la valeur la plus grande devrait être celle de la longueur. Ainsi, le périmètre s'écrit comme la somme des côtés.

$$ (x+17)+(x+9)+(x+17)+(x+9)=64 $$

$$ 2(x+17)+2(x+9)=64$$

Tu peux résoudre et trouver la valeur de x.

Pour le #7, il te faut faire attention à ce que valent tes variables. Ainsi, \(d=2r\) et \(r=\frac{d}{2}\).

$$ A_{disque}=\pi r^2=\pi(\frac{d}{2})^2 $$

Tu peux aussi trouver une expression pour l'aire du triangle et finaliser le calcul.

J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !