Secondary IV • 1yr.
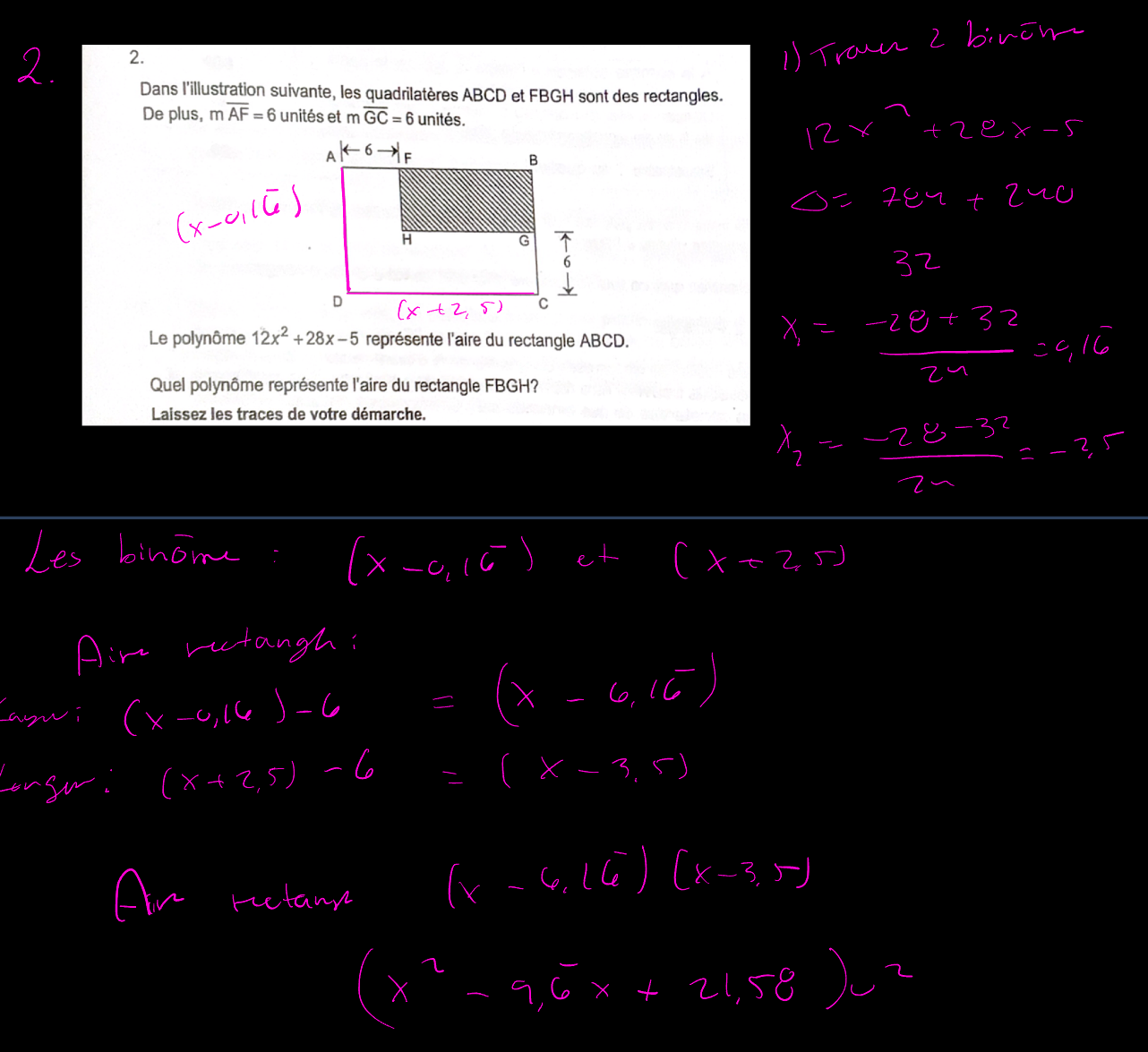
Bonjour, je ne comprend pas pourquoi je n'arrive pas à la bonne réponse, le corriger a utiliser la méthode somme-produit et moi la quadratique, est-ce que ses bon? Pouvez vous m'aider s.v.p?
Merci à l'avance!!






Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Salut!
Oui, tu peux utiliser la formule quadratique pour factoriser le polynôme. Cependant, il ne faut pas oublié d’ajouter le paramètre \(a\) dans le polynôme factorisé, comme ceci :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ainsi, puisque a=12, tu as le polynôme suivant :
$$12(x-0,1\overline{6})(x+2,50)$$
$$12(x-\frac{1}{6})(x+2,50)$$
On a donc trois facteurs, mais on n'en veut que deux, un pour la largeur et un pour la longueur. Nous devons donc éliminer un des facteurs. Pour cela, nous allons distribuer le facteur 12 sur les termes dans la parenthèse, ce qui nous donne ceci :
$$(12x-2) (x+2,5)$$
On factorise 2 :
$$2(6x-1) (x+2,5)$$
On distribue le facteur 2 sur la seconde paire de parenthèse afin d’éliminer le nombre décimal :
$$ (6x-1) (2x+5) $$
Voilà! On a maintenant deux facteurs et on a éliminé nos nombres décimaux. On a obtenu le même résultat que si on avait utilisé la technique du produit-somme.
Si tu as d’autres questions, n’hésite pas à nous réécrire! :)